Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

Rozważmy prostopadłościan $A B C D E F G H$ .

R6YbgO0HDGe0S

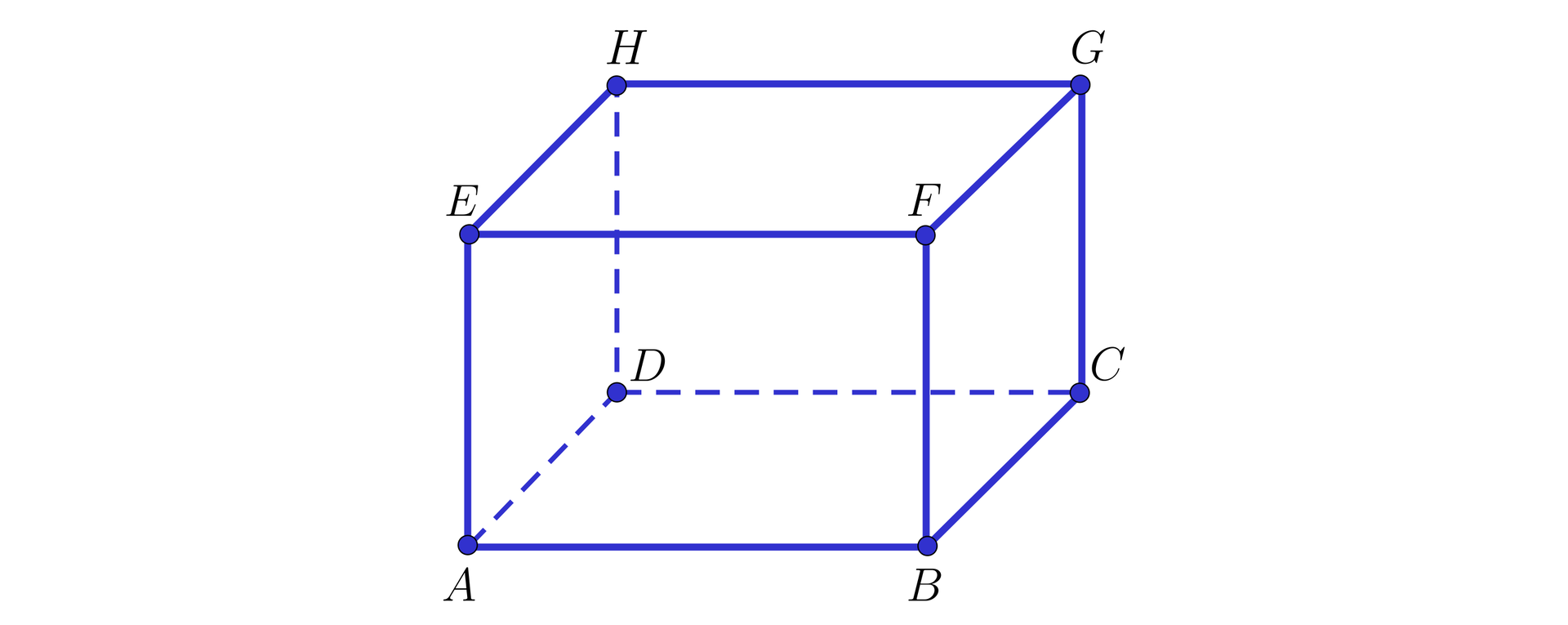
Ilustracja przedstawia prostopadłościan A B C D E F G H. Nad wierzchołkiem A znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F, nad wierzchołkiem C wierzchołek G i nad wierzchołkiem D wierzchołek H.

R12LgB4nSroWU

Ćwiczenie 2

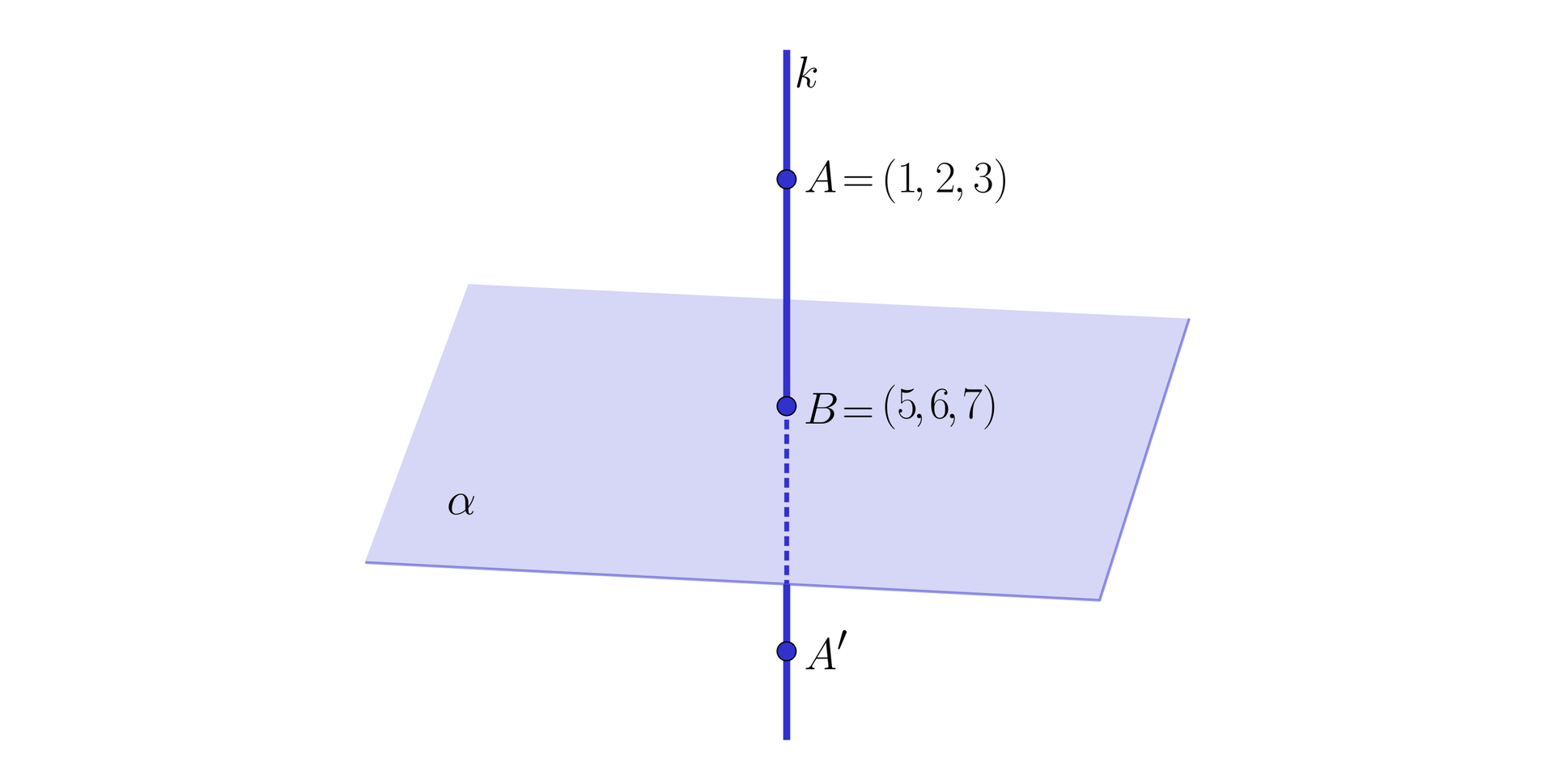
Prosta $k$ przebija płaszczyznę $α$ w punkcie $X$ .

Punkt $Y$ należy do prostej $k$ , a punkt $Y'$ jest rzutem prostokątnym punktu $Y$ na płaszczyznę $α$ .

Oblicz długość odcinka $X Y$ , jeżeli wiadomo, że $|X Y'| = 20$ i $|Y Y'| = 16$

R1I5jVkK080Ro

Uporządkuj poniższe zdania tak, aby otrzymać rozwiązanie tego zadania. Elementy do uszeregowania: 1. Zaczniemy jego rozwiązanie od sporządzenia rysunku i wypisania danych:

|X Y'| = 20

oraz

|Y Y'| = 16

., 2. Zauważmy, że trójkąt

Y Y' X

jest prostokątny., 3. Ostatecznie obliczamy, że

|X Y| = 4 \sqrt{41}

., 4. Wstawiając wartości

|X Y'| = 20

|Y Y'| = 16

dostajemy

{|X Y|}^{2} = 16^{2} + 20^{2}

., 5. Na mocy twierdzenia Pitagorasa otrzymujemy

{|Y Y'|}^{2} + {|X Y'|}^{2} = {|X Y|}^{2}

., 6. Stąd

|X Y| = \sqrt{256 + 400} = \sqrt{656}

Ćwiczenie 3

Prosta $k$ przebija płaszczyznę $α$ w punkcie $A$ .

Punkt $B$ należy do prostej $k$ .

Zakładając, że podane są:

długość odcinka $|A B|$
odległość punktu $B$ od płaszczyzny $α$

Oblicz długość odcinka będącego rzutem prostokątnym odcinka $A B$ na płaszczyznę $α$ .

R1354gcsfzbrt

Ćwiczenie 4

Rozważmy trójkąt $X Y Z$ taki, że $|X Y| = a$ , $|Y Z| = b$ , $|X Z| = c$ .

Punkty $X$ i $Y$ należą do płaszczyzny $α$ , a punkt $Z$ jest oddalony od płaszczyzny $α$ o $d$ .

Wyznacz długości boków trójkąta, który jest rzutem prostokątnym trójkąta $X Y Z$ na płaszczyznę $α$ .

Rzq5V78UpeXS7

Połącz w pary.

a = 7

b = 8

c = 9

d = 3

Możliwe odpowiedzi: 1.

2 \sqrt{2}

\sqrt{15}

2

, 2.

\sqrt{55}

7

6 \sqrt{2}

, 3.

\sqrt{3}

2

\sqrt{3}

, 4.

3

\sqrt{21}

2 \sqrt{3}

, 5.

3 \sqrt{17}

5

8 \sqrt{2}

a = 2

b = 3

c = 4

d = 1

Możliwe odpowiedzi: 1.

2 \sqrt{2}

\sqrt{15}

2

, 2.

\sqrt{55}

7

6 \sqrt{2}

, 3.

\sqrt{3}

2

\sqrt{3}

, 4.

3

\sqrt{21}

2 \sqrt{3}

, 5.

3 \sqrt{17}

5

8 \sqrt{2}

a = 3

b = 4

c = 5

d = 2

Możliwe odpowiedzi: 1.

2 \sqrt{2}

\sqrt{15}

2

, 2.

\sqrt{55}

7

6 \sqrt{2}

, 3.

\sqrt{3}

2

\sqrt{3}

, 4.

3

\sqrt{21}

2 \sqrt{3}

, 5.

3 \sqrt{17}

5

8 \sqrt{2}

a = 5

b = 12

c = 13

d = 4

Możliwe odpowiedzi: 1.

2 \sqrt{2}

\sqrt{15}

2

, 2.

\sqrt{55}

7

6 \sqrt{2}

, 3.

\sqrt{3}

2

\sqrt{3}

, 4.

3

\sqrt{21}

2 \sqrt{3}

, 5.

3 \sqrt{17}

5

8 \sqrt{2}

a = 2

b = 2

c = 2

d = 1

Możliwe odpowiedzi: 1.

2 \sqrt{2}

\sqrt{15}

2

, 2.

\sqrt{55}

7

6 \sqrt{2}

, 3.

\sqrt{3}

2

\sqrt{3}

, 4.

3

\sqrt{21}

2 \sqrt{3}

, 5.

3 \sqrt{17}

5

8 \sqrt{2}

Ćwiczenie 5

Prosta $k$ przebija płaszczyznę $α$ w punkcie $A$ i jest nachylona do tej płaszczyzny pod kątem $φ = 30 °$ .

Punkt $B$ należy do prostej $k$ oraz $|A B| = 18$ .

Oblicz długości odcinków $A C$ i $B C$ , gdzie $C$ jest rzutem prostokątnym punktu $B$ na płaszczyznę $α$ .

RVNtMocgl0LTn

Ćwiczenie 6

Na rysunku przedstawiono prostopadłościan $A B C D E F G H$ .

R1aZK65xF8D46

R1a4f4V0FnH4G

Ćwiczenie 7

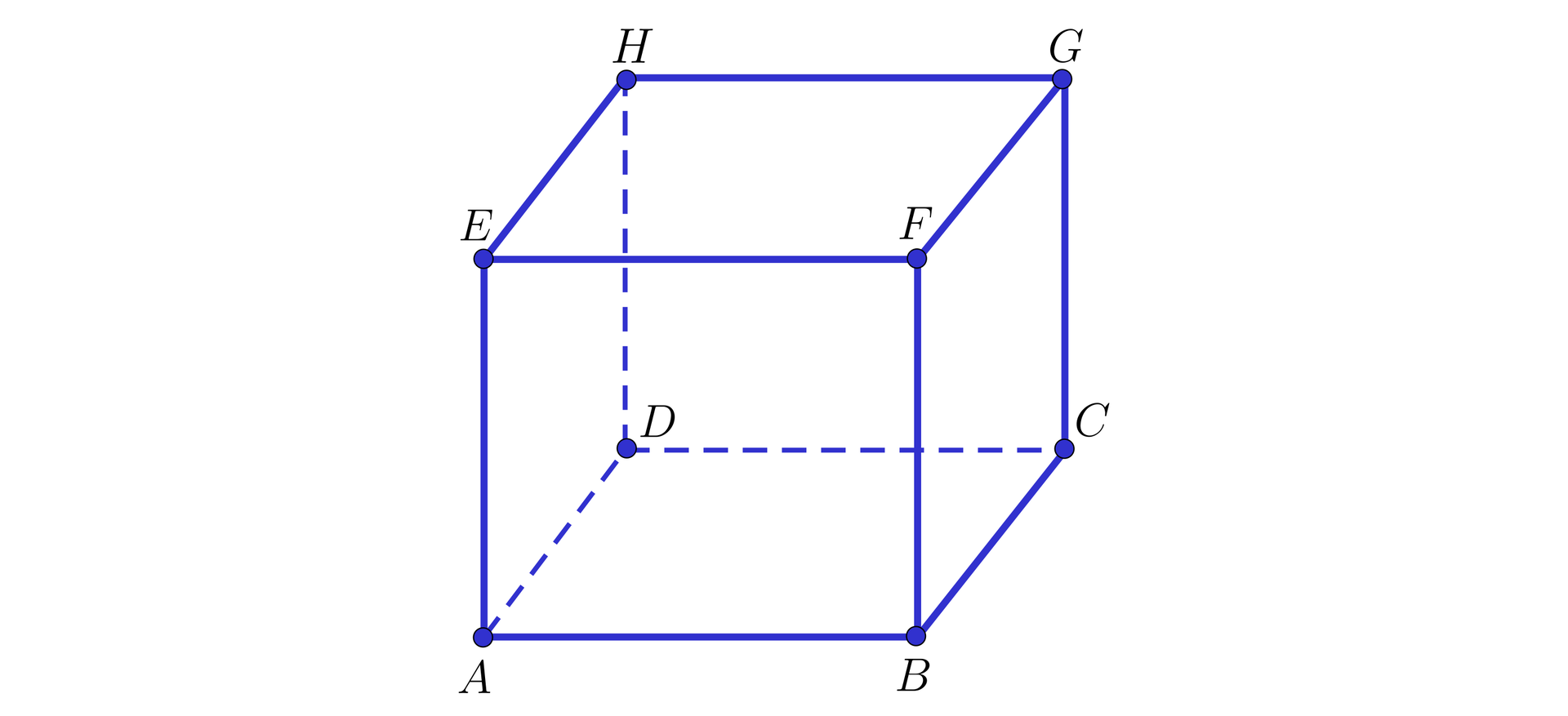
Rzutem punktu $A = (1, 2, 3)$ na pewną płaszczyznę $α$ jest punkt $B = (5, 6, 7)$ .

Wyznacz współrzędne punktu $A'$ symetrycznego do punktu $A$ względem płaszczyzny $α$ .

Rshk2K2pVrpLp

Ilustracja przedstawia płaszczyznę alfa przez którą przechodzi prosta k. Na prostej są zaznaczone trzy punkty, punkt: A, B i A prim. Punkt A ma współrzędne A=1,2,3. Punkt B leży na płaszczyźnie B=5,6,7. Pod płaszczyzną znajduje się punkt A prim który jest tak samo oddalony od punktu B co punkt A.

Zauważmy, że punkt $A'$ jest symetryczny do punktu $A$ względem płaszczyzny $α$ . Na mocy definicji punktów symetrycznych możemy stwierdzić, że punkt $B$ jest środkiem odcinka $A A'$ .

Niech $A' = (x, y, z)$ .

Wtedy korzystając ze wzorów na współrzędne środka odcinka otrzymujemy:

$\{\begin{cases} 5 = \frac{1 + x}{2} \\ 6 = \frac{2 + y}{2} \\ 7 = \frac{3 + z}{2} \end{cases}$

Zatem:

$\{\begin{cases} x + 1 = 10 \\ y + 2 = 12 \\ z + 3 = 14 \end{cases}$

$\{\begin{cases} x = 9 \\ y = 10 \\ z = 11 \end{cases}$

Czyli $A' = (9, 10, 11)$ .

Ćwiczenie 8

Punktem symetrycznym do punktu $A = (1, 0, - 2)$ względem pewnej płaszczyzny $α$ jest punkt $A' = (- 3, 4, 6)$ .

Wyznacz współrzędne rzutu prostokątnego $B$ punktu $A$ na płaszczyznę $α$ .

Jeżeli punkty $A$ i $A'$ są symetryczne względem płaszczyzny $α$ , a punkt $B$ jest rzutem prostokątnym punktu $A$ na tę płaszczyznę to jest on również środkiem odcinka $A A'$ .

Niech $B = (x, y, z)$ .

Wtedy korzystając ze wzorów na współrzędne środka odcinka dostajemy, że:

$\{\begin{cases} x = \frac{1 + (- 3)}{2} \\ y = \frac{0 + 4}{2} \\ z = \frac{- 2 + 6}{2} \end{cases}$

Zatem

$\{\begin{cases} x = \frac{1 - 3}{2} = \frac{- 2}{2} = - 1 \\ y = \frac{4}{2} = 2 \\ z = \frac{4}{2} = 2 \end{cases}$

Czyli $B = (- 1, 2, 2)$ .

Ćwiczenie 9

Wyznacz równanie prostej przechodzącej przez punkt $M (3, - 2, 4)$ i prostopadłej do płaszczyzny $α : 5 x + 3 y - 7 z + 1 = 0$ .

Wektorem normalnym płaszczyzny $α$ jest wektor $\vec{v} = [5, 3, - 7] = [A, B, C]$ .

Niech $p$ będzie szukaną prostą w przestrzeni równoległą do wektora $\vec{a} = [l, m, n]$ .

Prosta $p$ jest prostopadła do płaszczyzny $α$ wtedy i tylko wtedy, gdy:

$\{\begin{cases} A = λ l \\ B = λ m, gdzie λ \neq 0 \\ C = λ n \end{cases}$

Przyjmijmy $λ = 1$ .

Wtedy:

$\{\begin{cases} I = A \\ m = B \\ n = C \end{cases}$

Czyli $\vec{a} = \vec{v} = [A, B, C]$ .

Dlatego równanie parametryczne prostej $p$ jest postaci $(x_{0} = 3, y_{0} = - 2, z_{0} = 4)$ .

$p :$ $\{\begin{cases} x = 3 + 5 t \\ y = - 2 + 3 t, t \in ℝ \\ z = 4 - 7 t \end{cases}$

Równoważnie, prosta $p$ może być opisana przez równania kanoniczne (kierunkowe) postaci:

$p :$ $\frac{x - 3}{5} = \frac{y + 2}{3} = \frac{z - 4}{- 7}$ .

Ćwiczenie 10

Wyznacz rzut punktu $M (1, 2, - 3)$ na płaszczyznę $α : 6 x - y + 3 z - 41 = 0$ .

Równanie parametryczne prostej $p$ jest postaci:

$p :$ $\{\begin{cases} x = x_{0} + A t \\ y = y_{0} + B t, t \in ℝ \\ z = z_{0} + C t \end{cases}$

Zatem równanie parametryczne prostej $p$ przechodzącej przez punkt $M$ i prostopadłej do płaszczyzny $α$ ma postać:

$p :$ $\{\begin{cases} x = 1 + 6 t \\ y = 2 - t, t \in ℝ \\ 2 = - 3 + 3 t \end{cases}$

Szukany rzut $S$ punktu $M$ na płaszczyznę $α$ jest punktem przecięcia prostej $p$ i płaszczyzny $α$ , tzn. $S \in p \cap α$ .

Stąd w celu wyznaczenia współrzędnych punktu $S$ musimy rozwiązać następujący układ równań:

$\{\begin{cases} x = 1 + 6 t \\ y = 2 - t \\ z = - 3 + 3 t \\ 6 x - y + 3 z - 41 = 0 \end{cases}$

Wstawiając $x = 1 + 6 t$ , $y = 2 - t$ , $z = - 3 + 3 t$ do równania $6 x - y + 3 z - 41 = 0$ mamy:

$6 \cdot (1 + 6 t) - (2 - t) + 3 \cdot (- 3 + 3 t) - 41 = 0$

$6 + 36 t - 2 + t - 9 + 9 t - 41 = 0$

$46 t - 46 = 0$

$t = 1$

Stąd:

$\{\begin{cases} x = 1 + 6 t = 1 + 6 = 7 \\ y = 2 - t = 2 - 1 = 1 \\ z = - 3 + 3 t = - 3 + 3 = 0 \end{cases}$

Czyli punkt $S = (7, 1, 0)$ jest szukanym rzutem.

Ćwiczenie 11

Wyznacz punkt symetryczny do punktu $M (2, 7, 1)$ względem płaszczyzny $α : x - 4 y + z + 7 = 0$ .

Równanie parametryczne prostej $p$ jest postaci:

$p :$ $\{\begin{cases} x = x_{0} + A t \\ y = y_{0} + B t, t \in ℝ \\ z = z_{0} + C t \end{cases}$

Zatem równanie parametryczne prostej $p$ przechodzącej przez punkt $M$ i prostopadłej do płaszczyzny $α$ ma postać:

$p :$ $\{\begin{cases} x = 2 + t \\ y = 7 - 4 t, t \in ℝ \\ z = 1 + t \end{cases}$

Wyznaczamy rzut $S$ punktu $M$ na płaszczyznę $α$ , tzn. punkt przecięcia prostej $p$ i płaszczyzny $α$ , (czyli $S \in p \cap α$ ).

Stąd w celu wyznaczenia współrzędnych tego rzutu $S$ musimy rozwiązać następujący układ równań:

$\begin{array}{l} x = 2 + t \\ y = 7 - 4 t \\ z = 1 + t \\ x - 4 y + z + 7 = 0 \end{array}$

Stosując metodę podstawiania dostajemy:

$2 + t - 4 \cdot (7 - 4 t) + (1 + t) + 7 = 0$

$2 + t - 28 + 16 t + 1 + t + 7 = 0$

$18 t - 18 = 0$

$t = 1$

Stąd:

$\{\begin{cases} x = 2 + t = 2 + 1 = 3 \\ y = 7 - 4 t = 7 - 4 = 3 \\ z = 1 + t = 1 + 1 = 2 \end{cases}$

czyli $S = (3, 3, 2)$ jest rzutem punktu $M$ na płaszczyznę $α$ .

Niech $M' = (x, y, z)$ będzie punktem symetrycznym do $M$ względem płaszczyzny $α$ .

Wtedy rzut $S$ jest środkiem odcinka $M M'$ .

Zatem korzystając ze wzorów na współrzędne środka odcinka otrzymujemy, że:

$\{\begin{cases} 3 = \frac{2 + x}{2} \\ 3 = \frac{7 + y}{2} \\ 2 = \frac{1 + z}{2} \end{cases}$

$\{\begin{cases} 6 = x + 2 \\ 6 = y + 7 \\ 4 = z + 1 \end{cases}$

$\{\begin{cases} x = 4 \\ y = - 1 \\ z = 3 \end{cases}$

Czyli $M' = (4, - 1, 3)$ jest punktem symetrycznym do punktu $M$ względem płaszczyzny $α$ .

Aplet

Dla nauczyciela