Sprawdź się
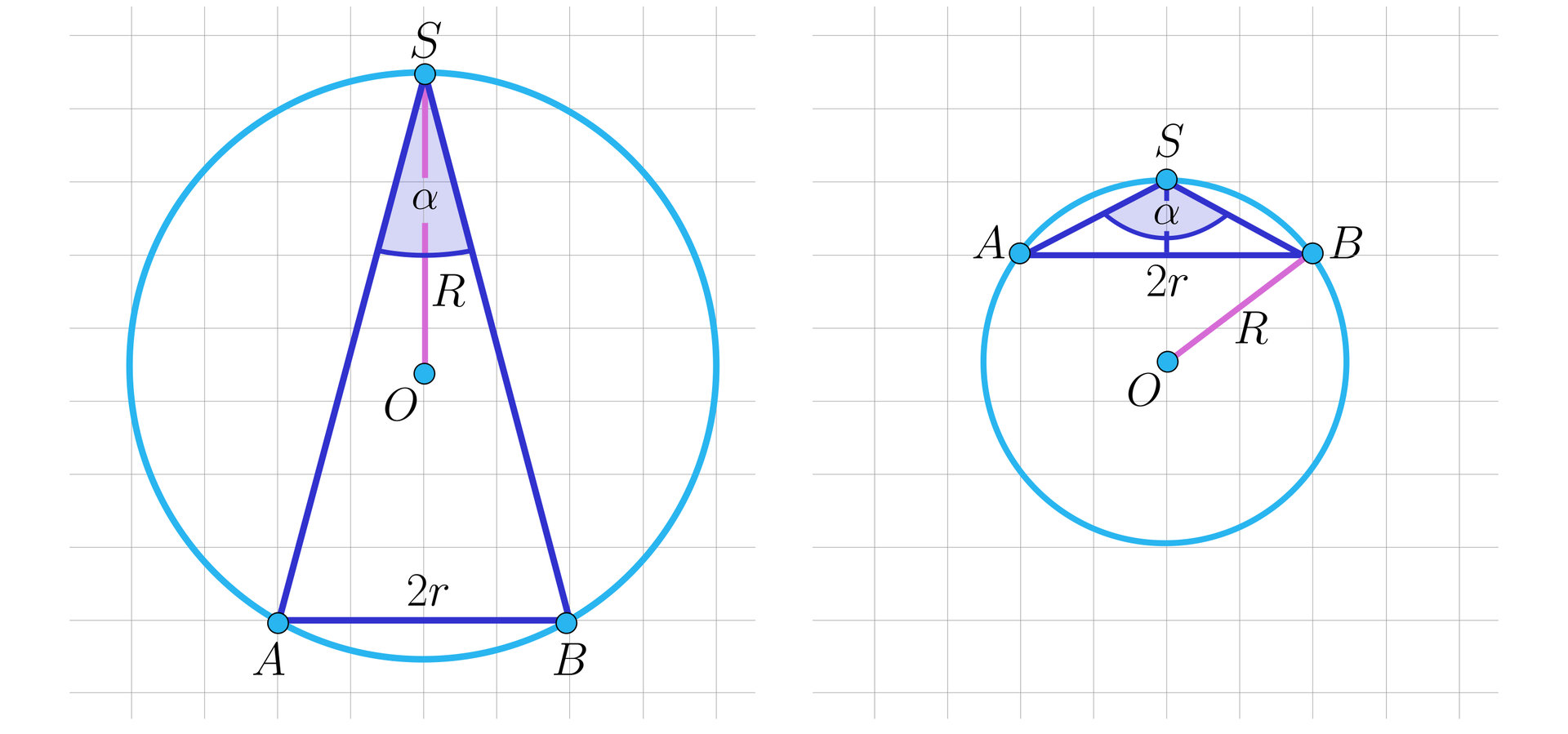
W kulę o promieniu długości wpisano stożek, którego kąt rozwarcia ma miarę .
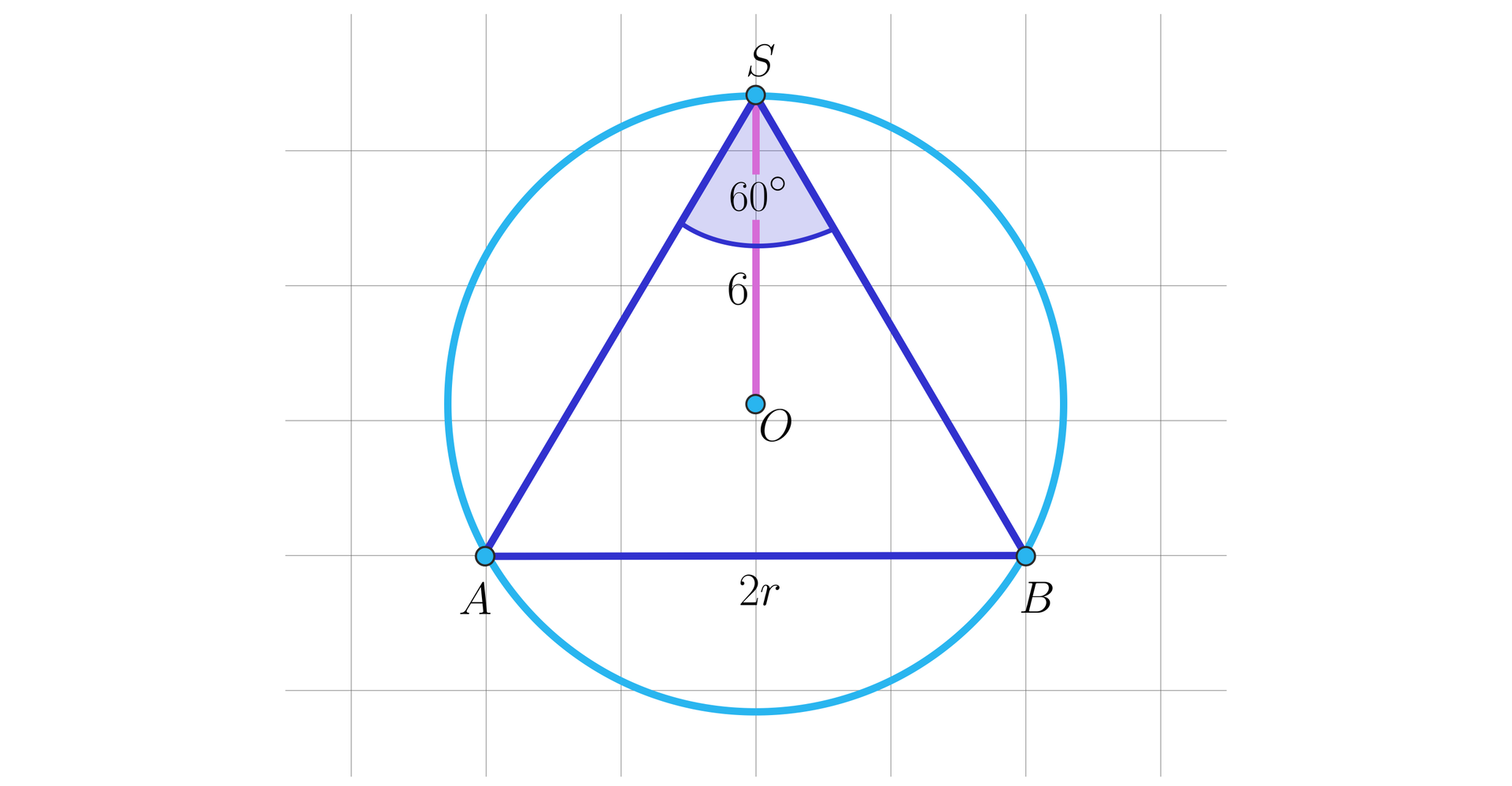
Oblicz długość podstawy stożka . Wynik podaj dokładnością do jedności.
............
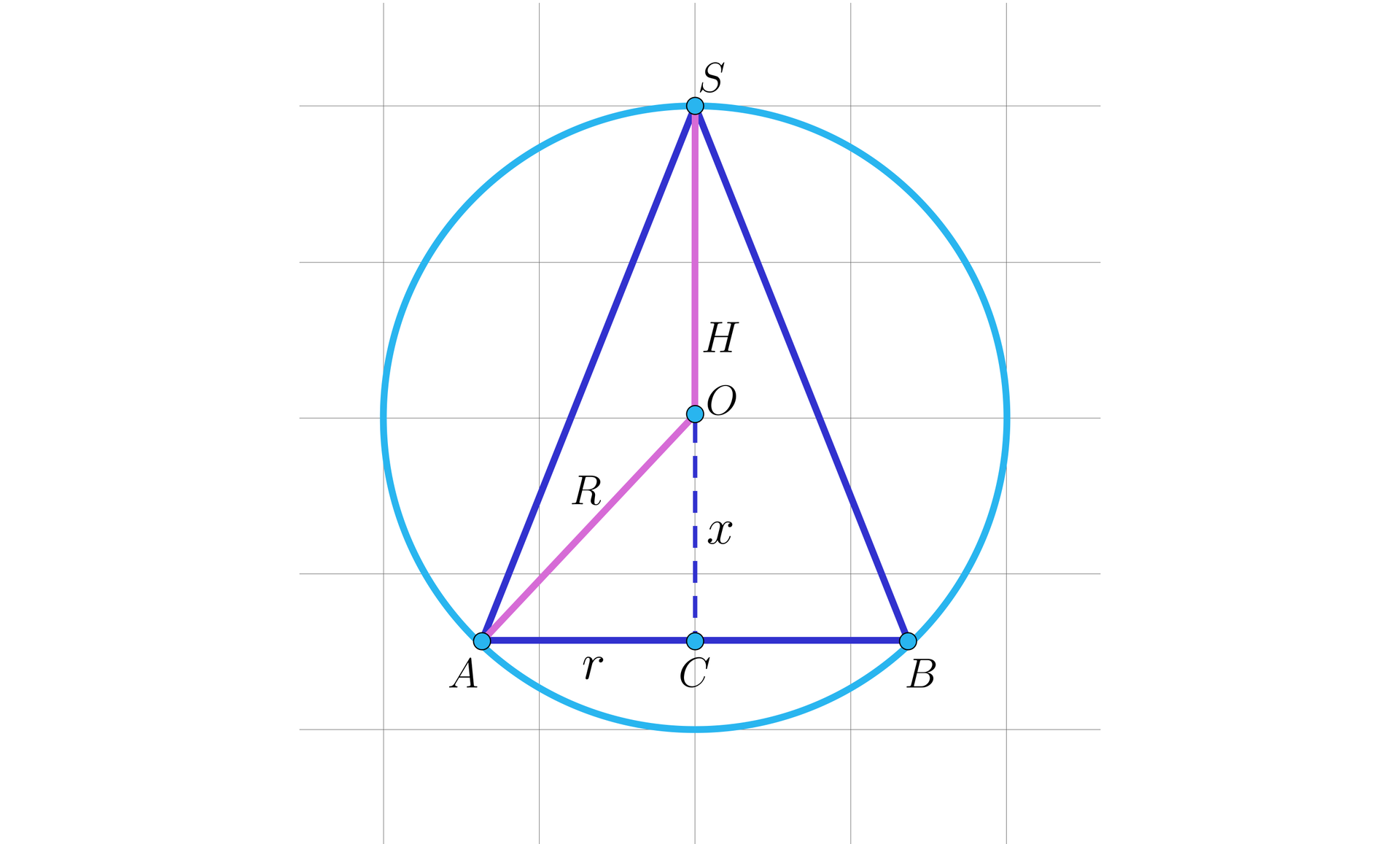
Kąt rozwarcia stożka wpisanego w kulę ma miarę . Prawdziwe są stwierdzenia:
- Środek kuli opisanej na stożku jest równocześnie środkiem koła będącego podstawą tego stożka.
- Wysokość stożka jest dłuższa od promienia kuli.
- Długość promienia podstawy stożka jest krótsza od długości promienia kuli.
- Wysokość stożka ma tę samą długość co promień kuli .
- Tworząca stożka ma długość , gdzie to długość promienia kuli.
- Objętość stożka jest cztery razy mniejsza od objętości kuli.
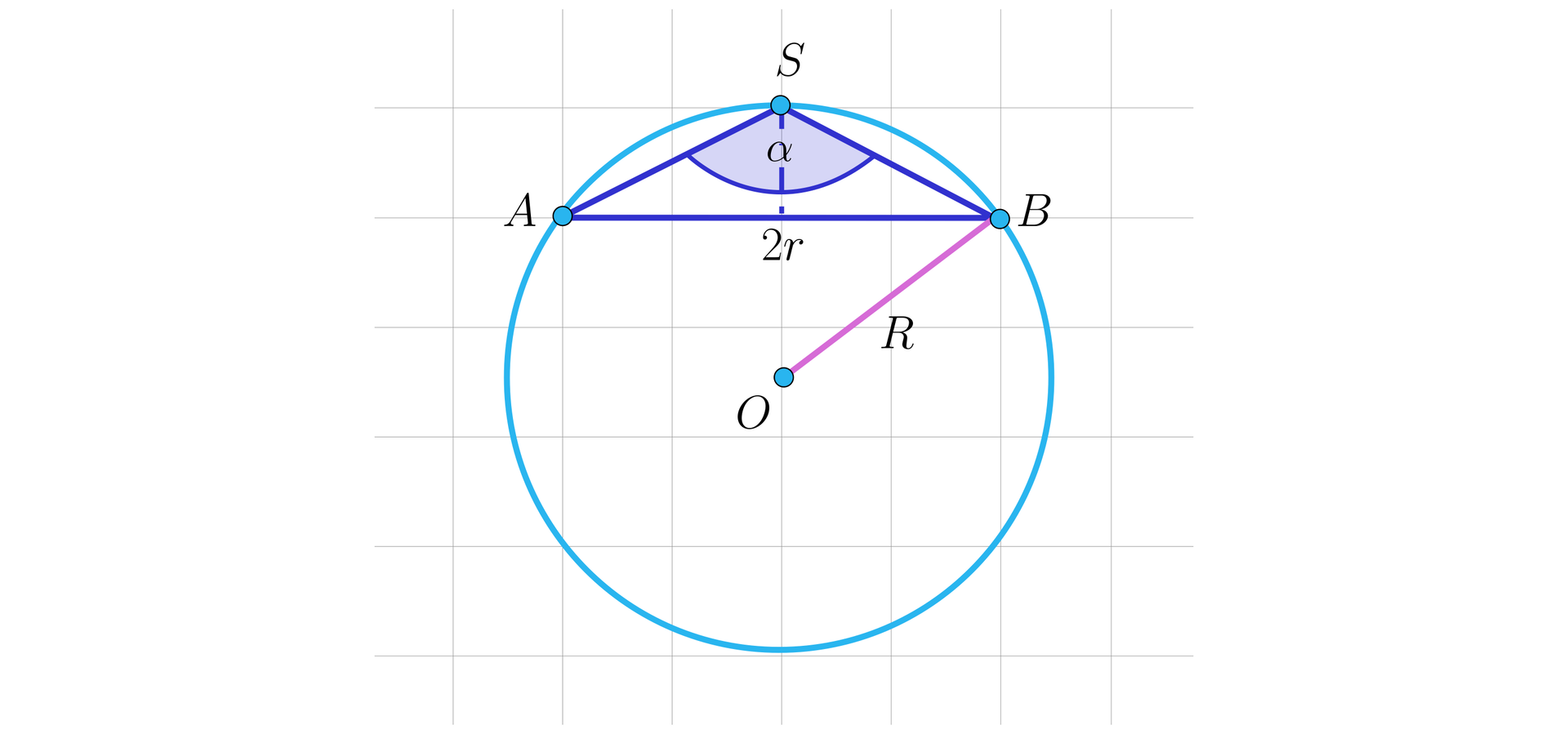
W kulę o promieniu długości wpisano stożek o promieniu podstawy długości . Kąt rozwarcia tego stożka może mieć miarę:
| Prawda | Fałsz | |
| □ | □ | |
| □ | □ | |
| lub | □ | □ |
| lub | □ | □ |
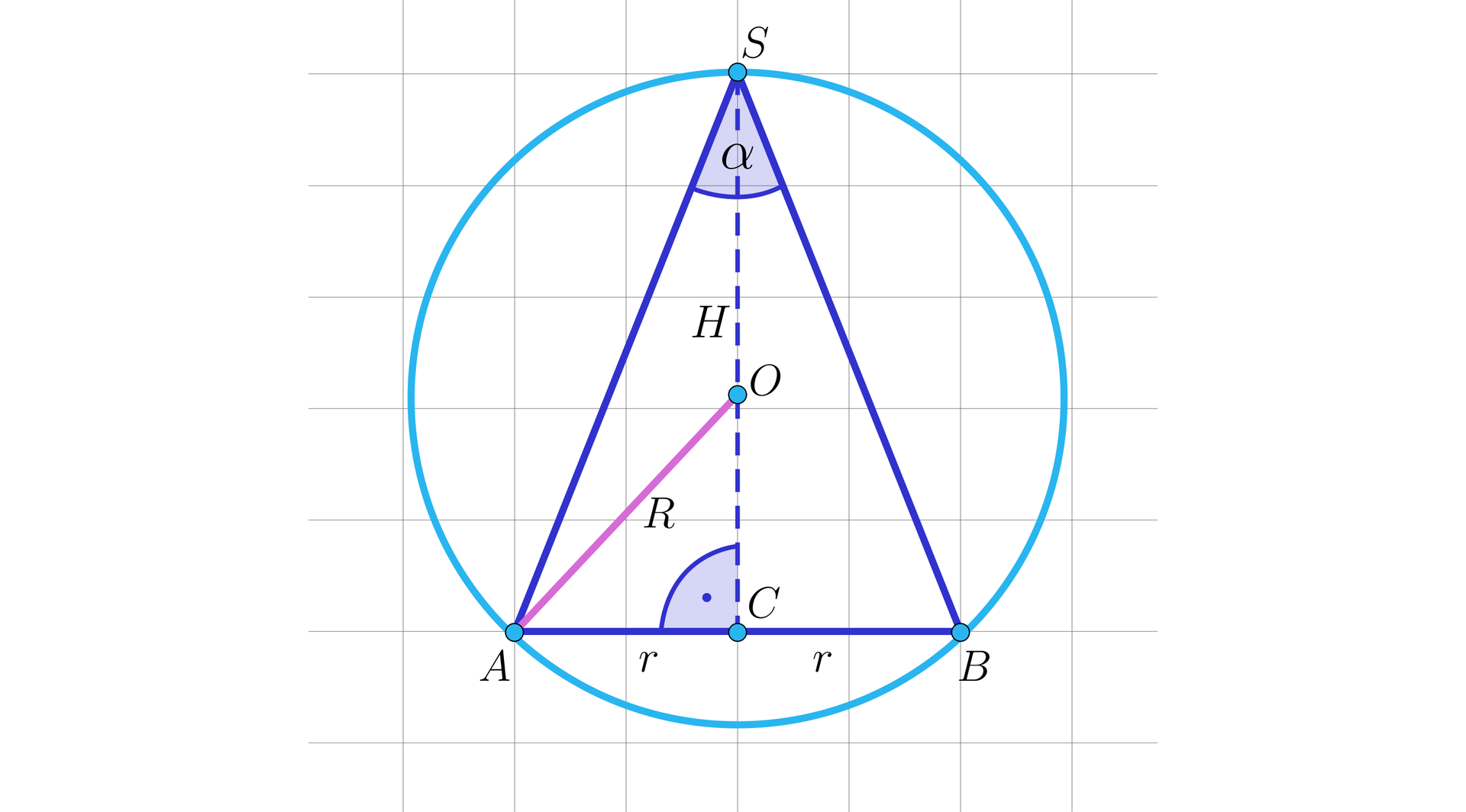
Tworząca stożka wpisanego w kulę jest nachylona do płaszczyzny podstawy pod kątem . Promień kuli ma długość .
Uzupełnij obliczenia przeciągając wyrażenia w odpowiednie miejsca.
(1) Kreślimy rysunek i przyjmujemy oznaczenia jak na rysunku:
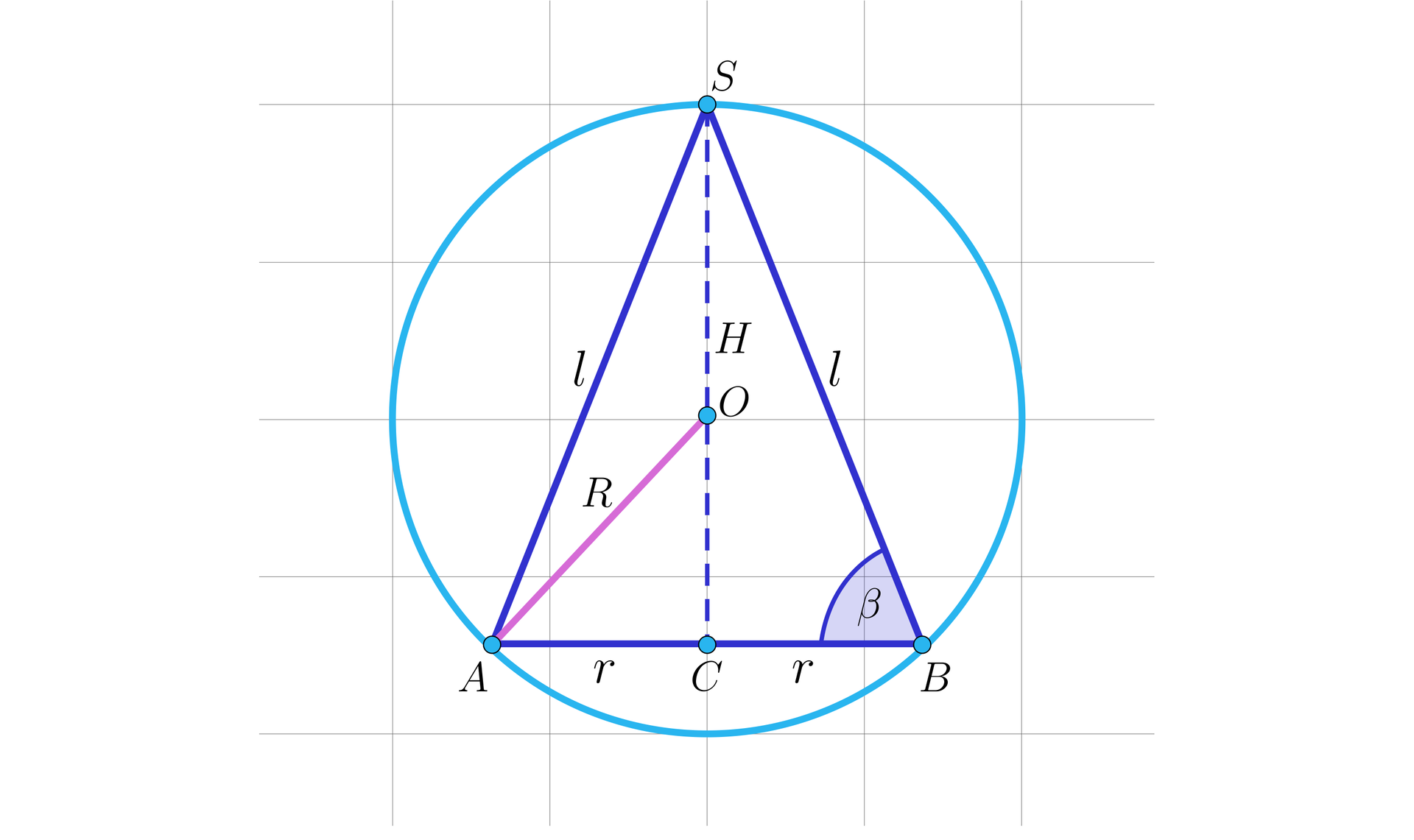
, , , ,
(2) Korzystając z twierdzenia sinusów w trójkącie wyznaczamy długość tworzącej stożka .................................. , zatem .
(3) Zauważmy, że kąt rozwarcia stożka ma miarę ...................................
(4) Długość promienia podstawy stożka wyznaczamy korzystając z twierdzenia sinusów w trójkącie , stąd .................................., zatem .
(5) Obliczamy pole powierzchni bocznej stożka ................................... Podstawiając do wzoru otrzymujemy ...................................
W kulę o promieniu długości wpisano stożek o kącie rozwarcia miary . Wyznacz objętość stożka.
W kulę wpisano stożek. Promień kuli, wysokość stożka oraz promień podstawy stożka mają tę samą długość. Wyznacz stosunek pola powierzchni kuli do pola powierzchni bocznej stożka.
Stosunek długości promienia kuli opisanej na stożku do długości wysokości stożka wynosi . Oblicz stosunek objętości kuli do objętości stożka.