Sprawdź się

Pokaż ćwiczenia:

Ćwiczenie 1

R1Tgng5FVB6yC

Postacią ogólną wzoru funkcji kwadratowej $f$ danej wzorem $f (x) = - \frac{1}{2} {(x - \frac{1}{3})}^{2} + \frac{1}{6}$ jest:

$f (x) = - \frac{1}{2} x^{2} + \frac{1}{3} x + \frac{1}{9}$
$f (x) = - \frac{1}{2} x^{2} - \frac{1}{3} x - \frac{1}{9}$
$f (x) = \frac{1}{2} x^{2} + \frac{1}{3} x - \frac{1}{9}$

Ćwiczenie 2

RBAweLE25nHab

Połącz w pary wzór funkcji kwadratowej podany w postaci kanonicznej z odpowiadającymi mu współczynnikami $a, b, c$ , po rozwinięciu do postaci ogólnej wzoru funkcji kwadratowej $f (x) = a x^{2} + b x + c$ :

$f (x) = - 3 {(x - 1)}^{2} - 4$
$f (x) = 2 {(x + 3)}^{2} - 1$
$f (x) = - {(x - 5)}^{2} - 2$
$f (x) = 4 {(x - 1)}^{2} + 3$

Ćwiczenie 3

Na rysunku przedstawiono wykres funkcji kwadratowej $f$ .

RfUhn1Z0UCWax

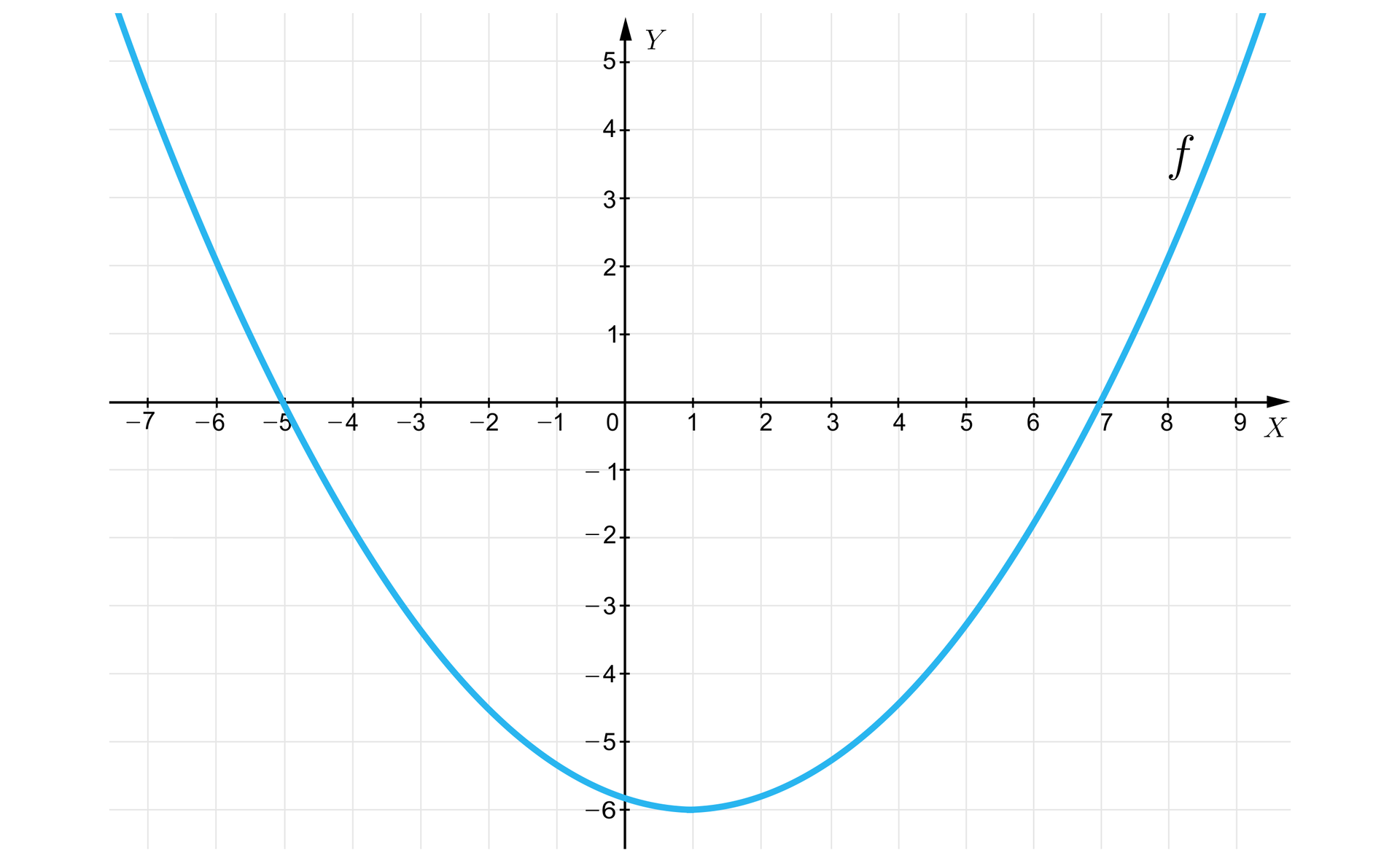
Ilustracja przedstawia pozioma oś X od minus siedmiu do dziewięciu oraz pionową oś Y od minus sześciu do pięciu. Na rysunku zaznaczono także wykres funkcji kwadratowej będącej parabolą o wierzchołku w punkcie nawias jeden średnik minus sześć koniec nawiasu oraz z ramionami skierowanymi w górę. Wykres funkcji ma dwa miejsca zerowe w punktach nawias minus pięć średnik zero koniec nawiasu oraz nawias siedem średnik zero koniec nawiasu.

Zaznacz zdania, które są prawdziwe.

R1YhscGJcLJqP

Funkcję $f$ przedstawioną na wykresie opisujemy za pomocą wzoru $f (x) = \frac{1}{6} {(x - 1)}^{2} - 6$ .
Współrzędne wierzchołka paraboli, będącej wykresem funkcji $f$ wynoszą $(- 1, 6)$ .
Osią symetrii paraboli, będącej wykresem funkcji $f$ jest prosta o równaniu $x = - 1$ .
Funkcję $f$ , której wykres przedstawiono na rysunku opisujemy za pomocą wzoru $f (x) = \frac{1}{6} x^{2} - \frac{1}{3} x - \frac{35}{6}$ .

Ćwiczenie 4

RwO52tNPEH5xn

Wstaw w tekst odpowiednie liczby.

$\frac{15}{7}$ , $2$ , $\frac{1}{4}$ , $\frac{23}{8}$ , $f (x) = 2 {(x - \frac{1}{4})}^{2} + \frac{23}{8}$ , $f (x) = 2 {(x + \frac{1}{4})}^{2} - \frac{23}{8}$ , $\frac{1}{2}$

Dana jest funkcja kwadratowa $f$ określona wzorem $f (x) = a x^{2} - x + 3$ . Wiadomo, że funkcja jest malejąca w maksymalnym przedziale $(- \infty, \frac{1}{4}"⟩"$ .
Zatem:
$p =$ ..........................
$a =$ ..........................
$q =$ ..........................
Postać kanoniczna wzoru tej funkcji wyraża się wzorem ...........................

Ćwiczenie 5

Rm0VRxJPh3tvl

Pogrupuj elementy, zgodnie z podanym opisem.

osią symetrii paraboli, będącej wykresem funkcji <math><mi>f</mi></math> jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mo>-</mo><mn>1</mn></math>, postać ogólna wzoru funkcji <math><mi>f</mi></math> wynosi <math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mn>3</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>6</mn><mi>x</mi><mo>+</mo><mn>1</mn></math>, osią symetrii paraboli, będącej wykresem funkcji <math><mi>f</mi></math> jest prosta o równaniu <math><mi>x</mi><mo>=</mo><mn>1</mn></math>, wierzchołek wykresu ma współrzędne <math><mfenced><mrow><mn>1</mn><mo>,</mo><mn>2</mn></mrow></mfenced></math>, postać ogólna wzoru funkcji <math><mi>f</mi></math> wynosi <math><mi>f</mi><mfenced><mi>x</mi></mfenced><mo>=</mo><mo>-</mo><mn>3</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>6</mn><mi>x</mi><mo>-</mo><mn>1</mn></math>, wierzchołek wykresu ma współrzędne <math><mfenced><mrow><mo>-</mo><mn>1</mn><mo>,</mo><mo>-</mo><mn>2</mn></mrow></mfenced></math>

Własności funkcji kwadratowej $f$ określonej wzorem $f (x) = 3 {(x + 1)}^{2} - 2$ :
Własności funkcji kwadratowej $f$ określonej wzorem $f (x) = - 3 {(x - 1)}^{2} + 2$ :

Ćwiczenie 6

RATEN9kxn8toh

Jeżeli funkcja kwadratowa $f$ jest określona wzorem w postaci kanonicznej $f (x) = - \frac{1}{3} {(x - 3)}^{2} + 1$ , to iloczyn współczynników $a \cdot b \cdot c$ ze wzoru w postaci ogólnej $f (x) = a x^{2} + b x + c$ wynosi:

$\frac{4}{3}$
$- \frac{4}{3}$
$\frac{8}{3}$

Ćwiczenie 7

Zapisz wzór funkcji kwadratowej $f (x) = - 2 x^{2} + b x - 6$ w postaci kanonicznej, jeżeli pierwsza współrzędna wierzchołka paraboli, będącej wykresem tej funkcji wynosi $(- 1)$ .

Korzystając ze wzoru $p = \frac{- b}{2 a}$ , w celu wyznaczenia wartości $b$ , rozwiązujemy równanie:

$- 1 = \frac{- b}{2 \cdot (- 2)}$ .

Zatem $b = - 4$ .

Wobec tego:

$f (x) = - 2 x^{2} - 4 x - 6$ , zatem

$q = f (- 1) = - 2 \cdot {(- 1)}^{2} - 4 \cdot (- 1) - 6 = - 4$ .

Postać kanoniczna wyraża się wzorem $f (x) = - 2 {(x + 1)}^{2} - 4$ .

Ćwiczenie 8

Wyznacz współczynniki $b$ i $c$ ze wzoru funkcji kwadratowej określonej wzorem $f (x) = x^{2} + b x + c$ , jeżeli wierzchołkiem jej wykresu jest punkt o współrzędnych $(- 2, 3)$ .

Zauważmy, że $a = 1$ .

Ponieważ punkt o współrzędnych $(- 2, 3)$ jest wierzchołkiem wykresu funkcji z zadania, zatem postać kanoniczna wyraża się wzorem:

$f (x) = {(x + 2)}^{2} + 3$ .

Po zamianie tego wzoru na postać ogólną mamy:

$f (x) = {(x + 2)}^{2} + 3 = x^{2} + 4 x + 4 + 3 = x^{2} + 4 x + 7$ .

Zatem $b = 4$ i $c = 7$ .

Galeria zdjęć interaktywnych

Dla nauczyciela