Sprawdź się
Prostokąt wpisany jest w okrąg o promieniu . Długość boku .
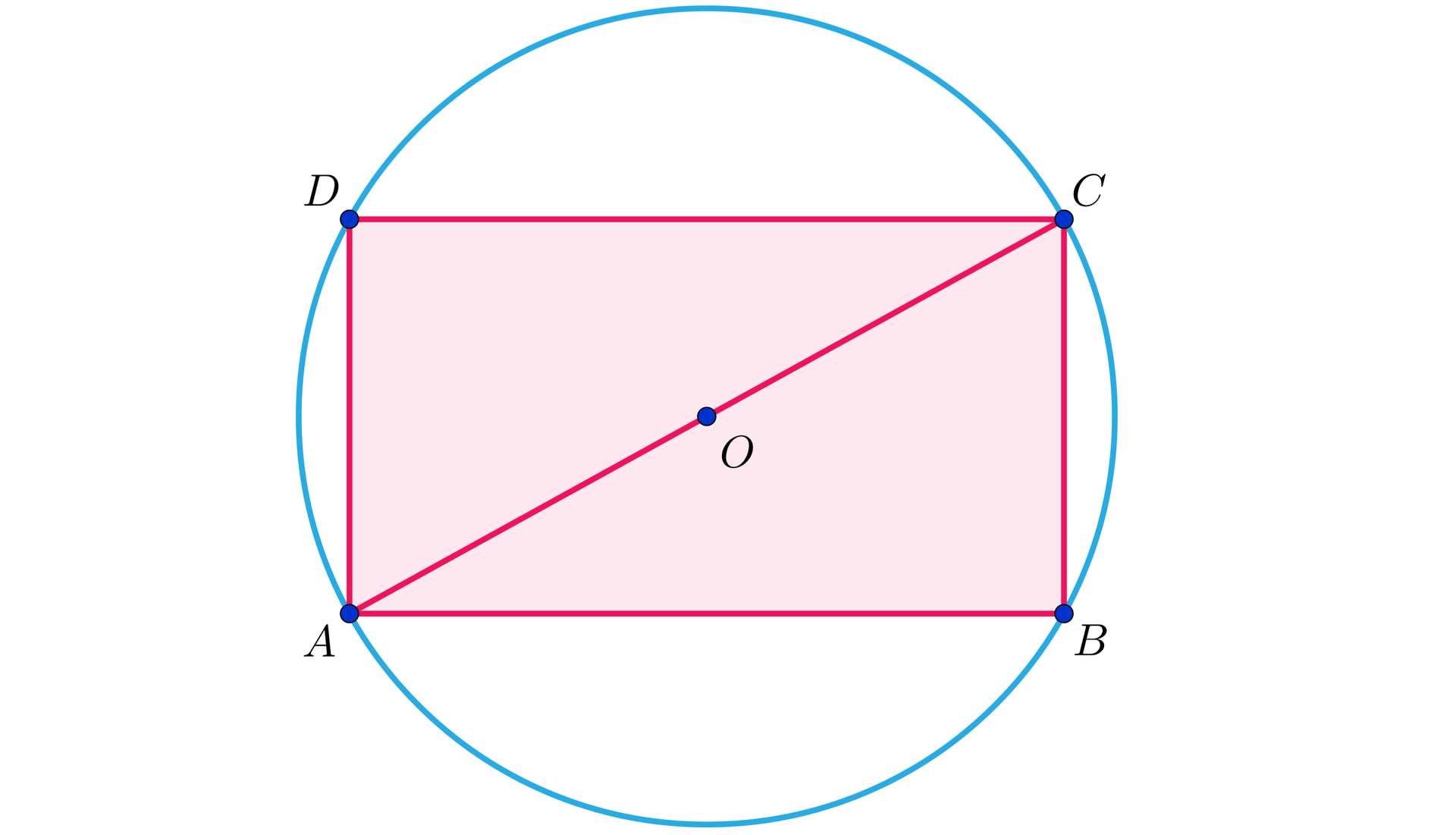
Jakie jest pole tego prostokąta?
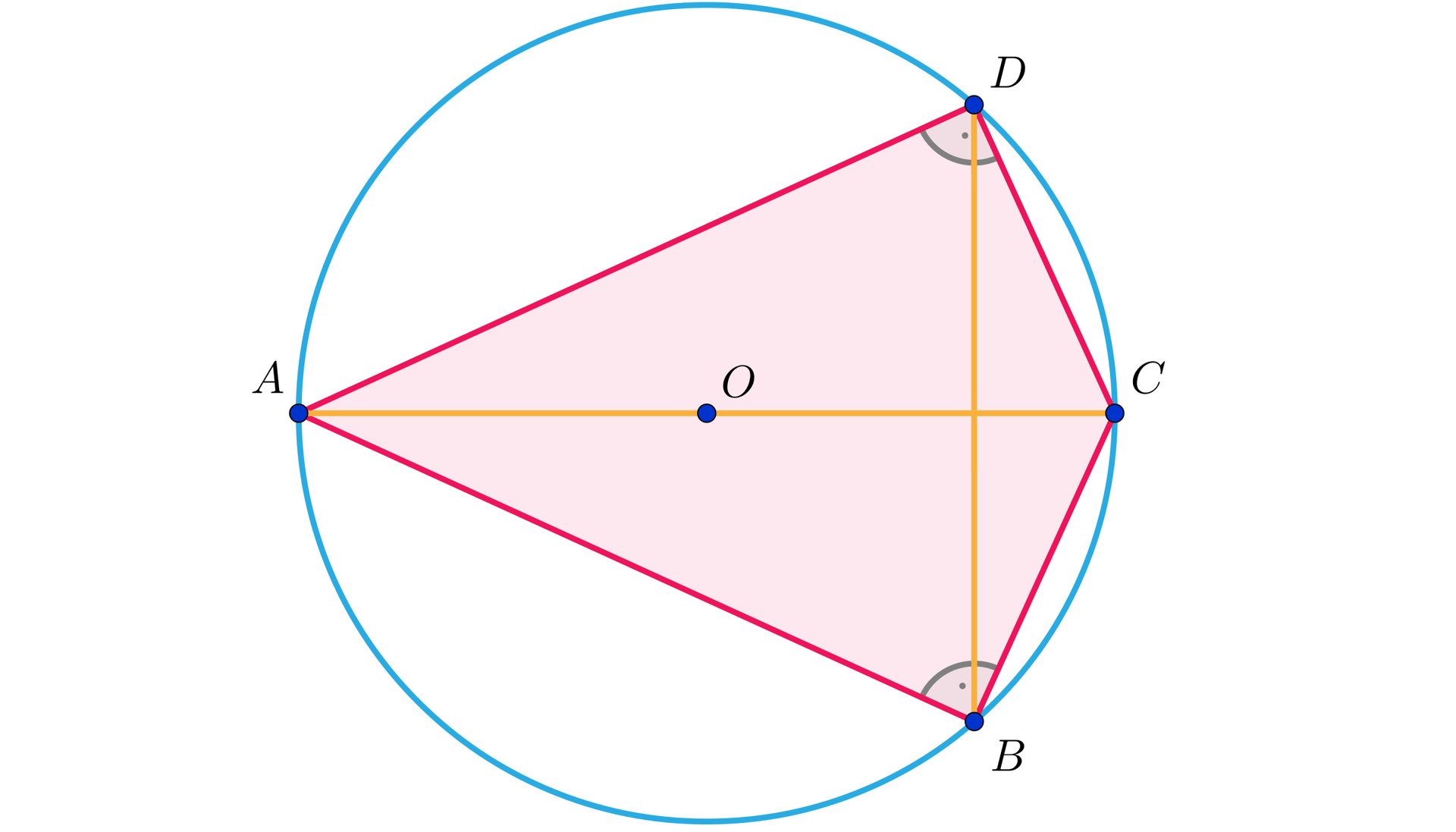
Udowodnij, że jeżeli na deltoidzie o bokach i można opisać okrąg, to jego pole wyraża się wzorem .
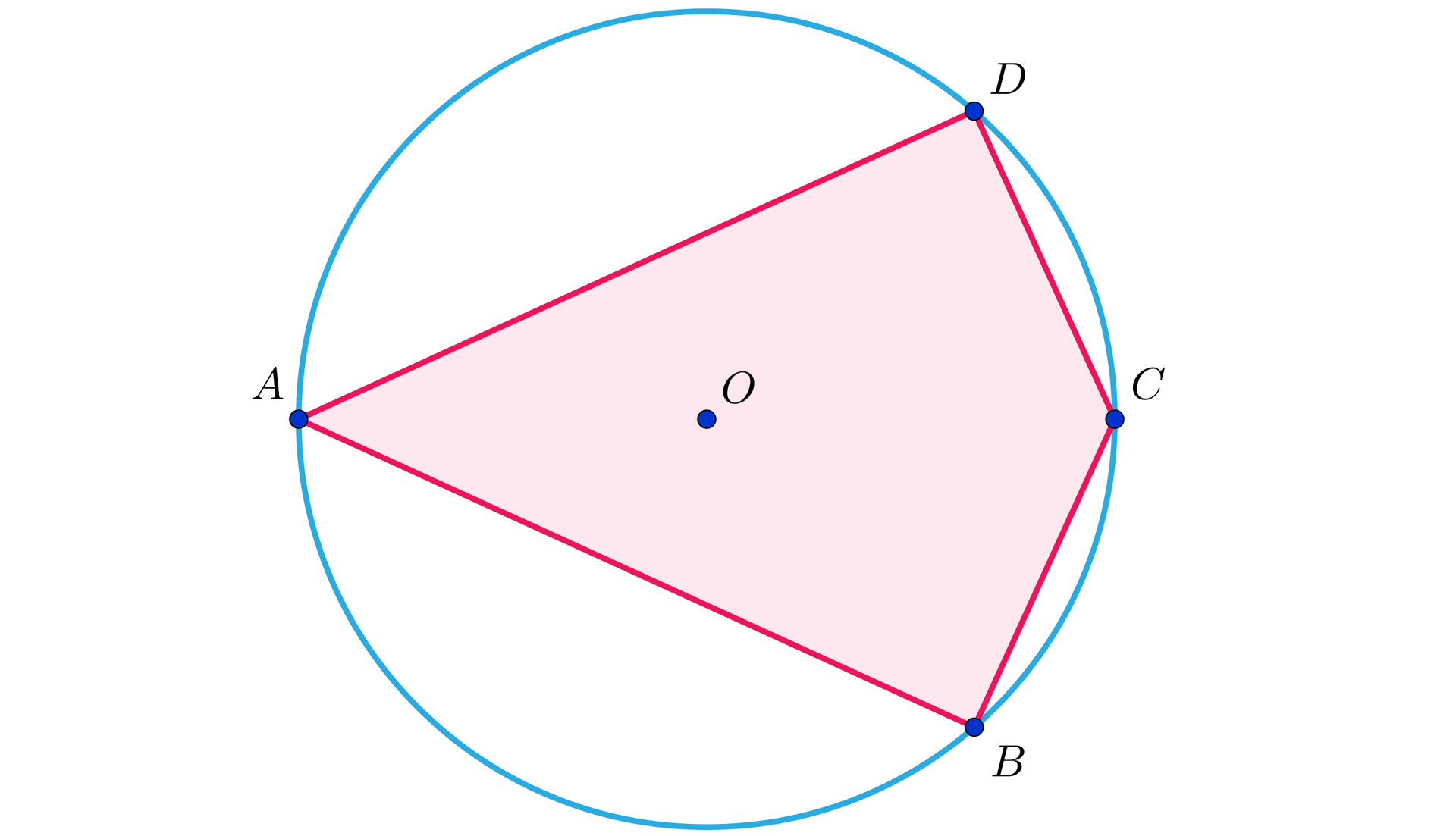
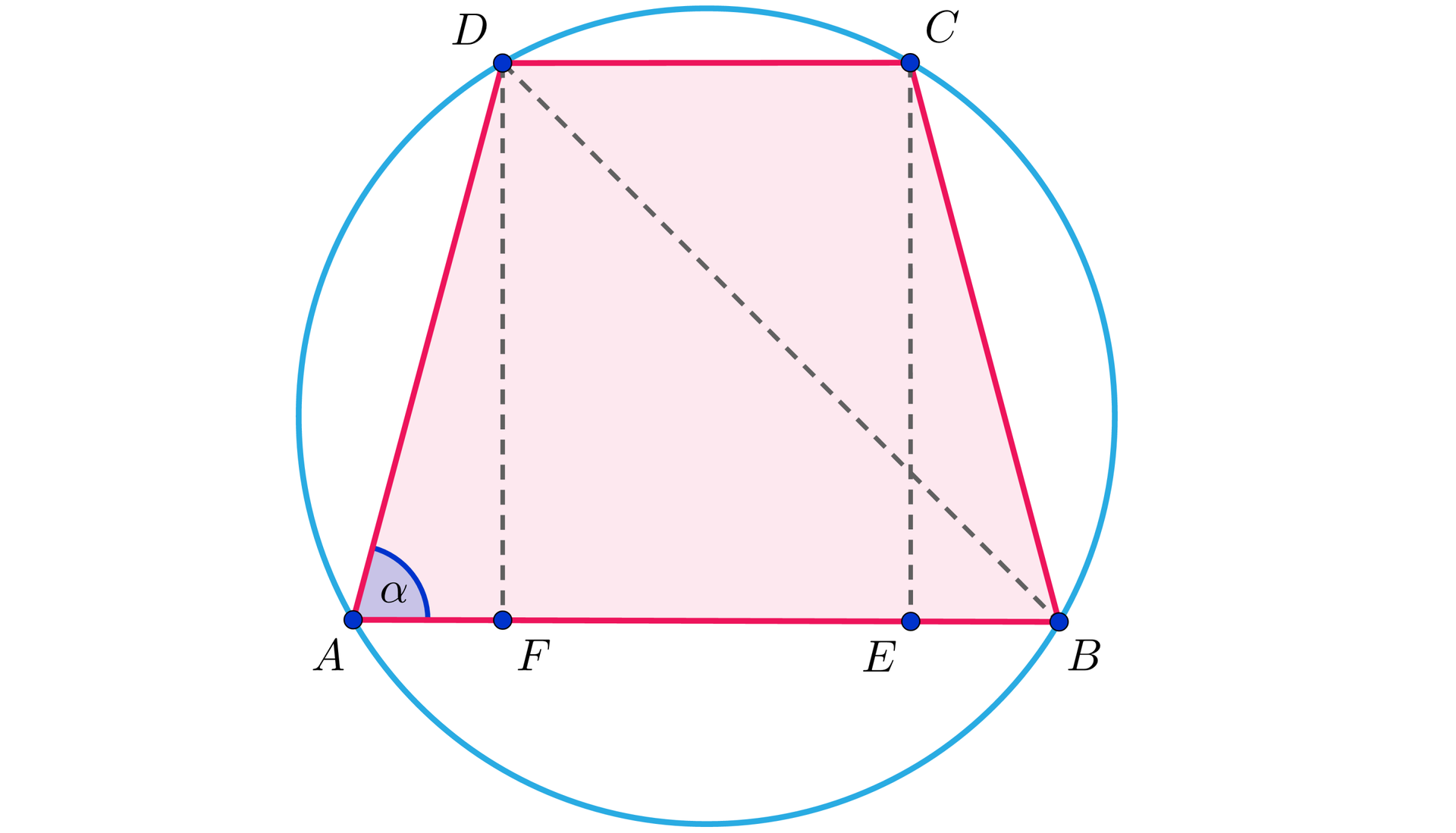
W trapezie wpisanym w okrąg jedna z podstaw jest dwa razy dłuższa od drugiej, a przekątna jest dwusieczną kąta przy dłuższej podstawie. Oblicz pole tego trapezu, jeżeli jego ramię ma długość .
Przekątne trapezu wpisanego w okrąg są prostopadłe. Wysokość tego trapezu jest równa . Wskaż zdania prawdziwe.
- Za mało jest danych, aby obliczyć pole tego trapezu.
- Pole jest równe .
- Przekątne tego trapezu są równej długości.
- Można wyznaczyć sumę długości podstaw trapezu.
- Nie można wyznaczyć sumy długości podstaw trapezu.
- Pole jest równe .
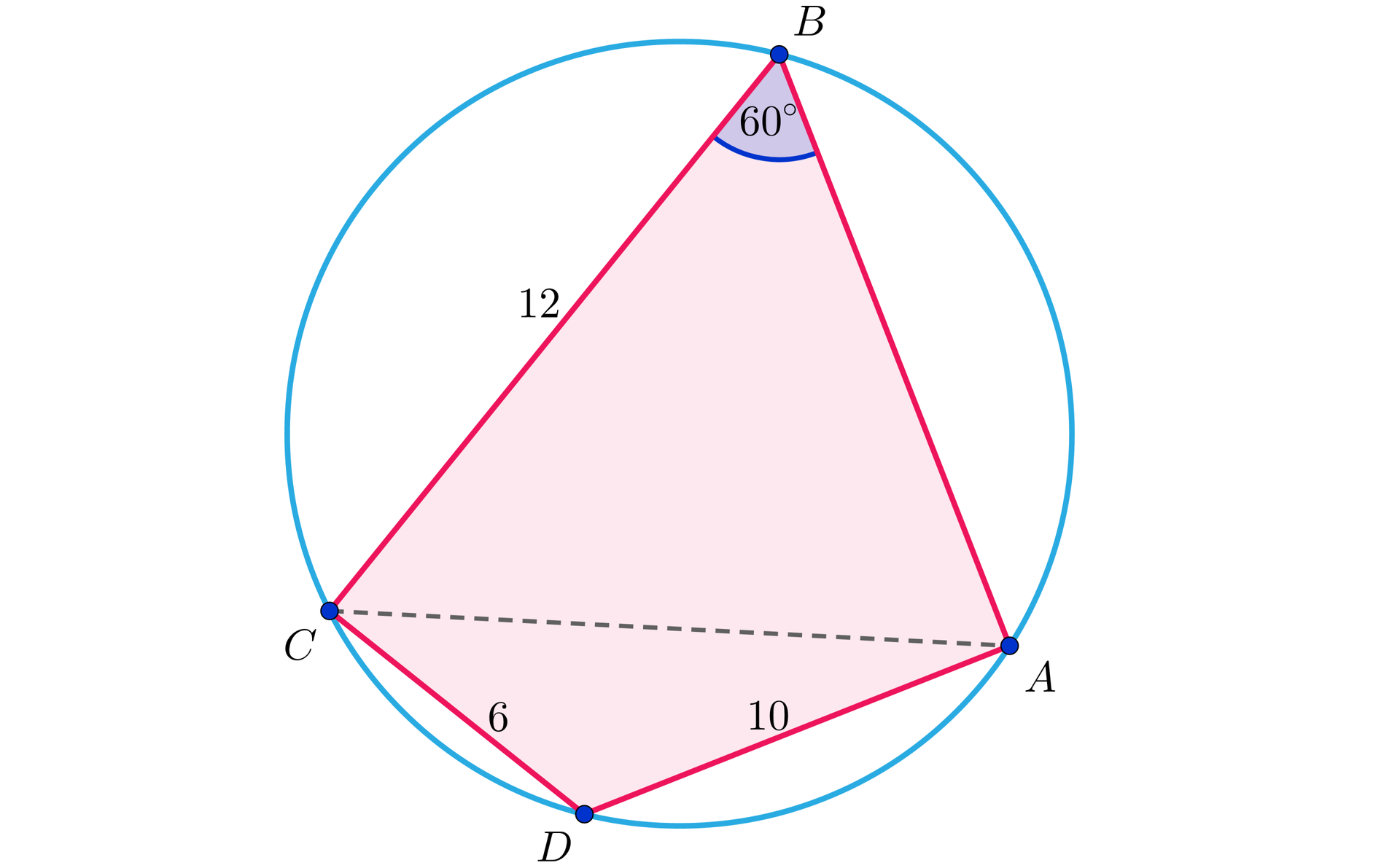
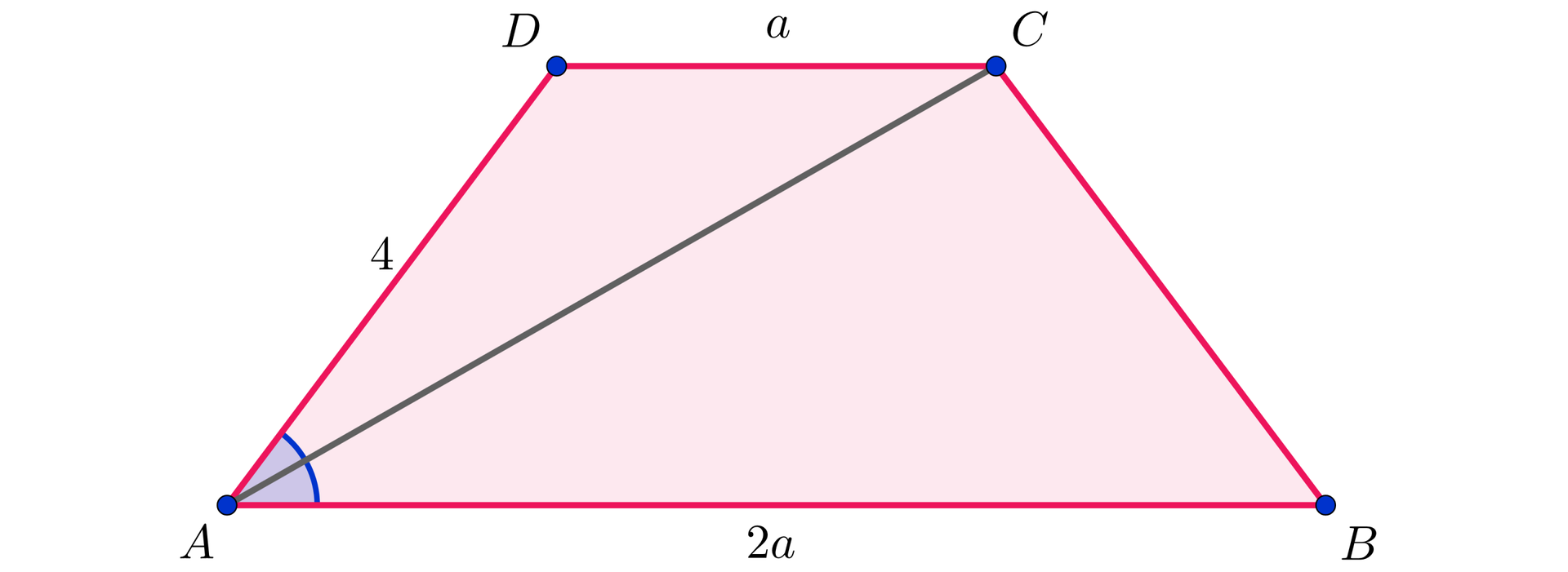
Uporządkuj etapy rozumowania prowadzącego do wyznaczenia pola tego czworokąta. Elementy do uszeregowania: 1. Podstawiając dane do powyższego równania wyznaczamy ., 2. Rozważmy teraz trójkąt ., 3. Pole czworokąta jest więc równe ., 4. , 5. Pole trójkąta jest równe ., 6. Ponieważ suma przeciwległych kątów w czworokącie opisanym na okręgu jest równa , więc kąt przy wierzchołku ma miarę ., 7. Na wstępie zauważmy, że podane długości boków trójkąta pozwalają, z twierdzenia cosinusów obliczyć cosinus kąta ., 8. Ponadto , więc jest to trójkąt równoboczny o boku długości ., 9. Znając kąt przy wierzchołku obliczamy pole trójkąta ., 10. , 11. Oznacza to, że kąt przy wierzchołku ma miarę .
Na czworokącie wypukłym można opisać okrąg. Wiadomo, że , , , .
Uporządkuj etapy rozumowania prowadzącego do wyznaczenia pola tego czworokąta.
- Na wstępie zauważmy, że podane długości boków trójkąta pozwalają, z twierdzenia cosinusów obliczyć cosinus kąta .
- Oznacza to, że kąt przy wierzchołku ma miarę .
- Pole czworokąta jest więc równe .
- Znając kąt przy wierzchołku obliczamy pole trójkąta .
- Rozważmy teraz trójkąt .
- Ponadto , więc jest to trójkąt równoboczny o boku długości .
- Pole trójkąta jest równe .
- Ponieważ suma przeciwległych kątów w czworokącie opisanym na okręgu jest równa , więc kąt przy wierzchołku ma miarę .
- Podstawiając dane do powyższego równania wyznaczamy .
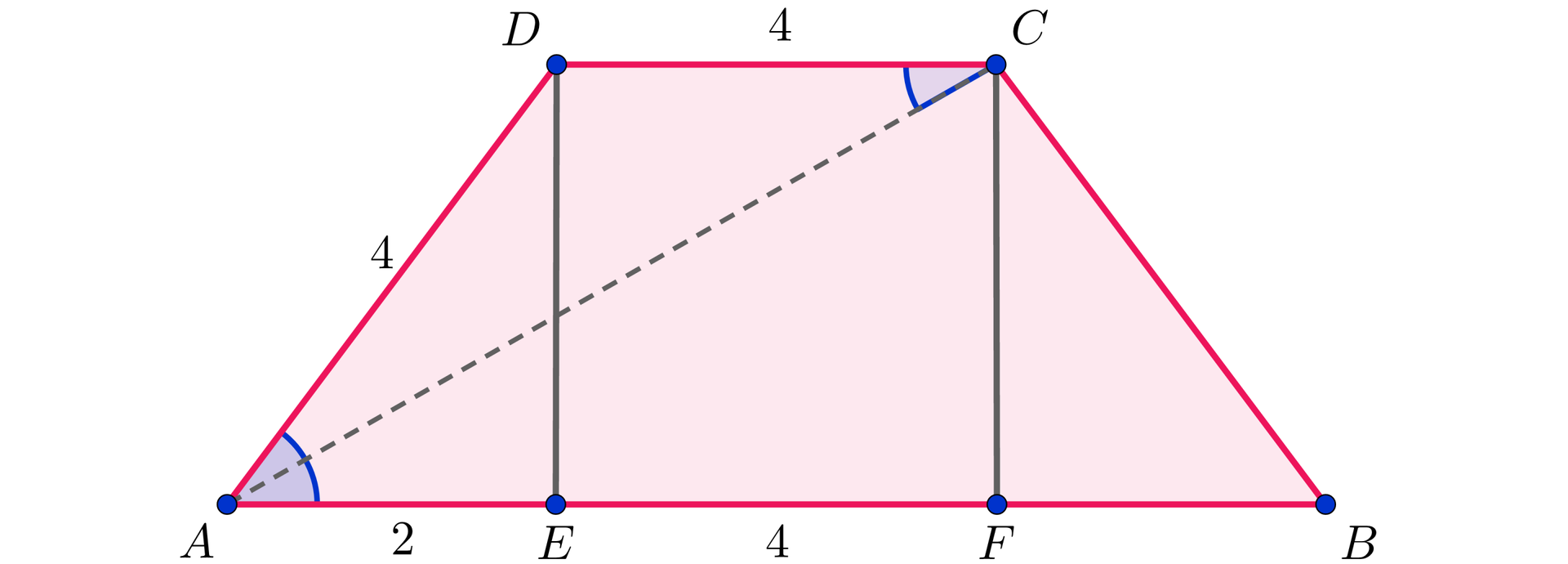
Obwód trapezu wpisanego w okrąg wynosi . Wysokość , poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach i . Połącz w pary - daną wielkość i odpowiadającą jej liczbę.
<span aria-label="osiem" role="math"><math><mn>8</mn></math></span>, <span aria-label="cztery" role="math"><math><mn>4</mn></math></span>, <span aria-label="czterdzieści cztery" role="math"><math><mn>44</mn></math></span>, <span aria-label="pięć" role="math"><math><mn>5</mn></math></span>, <span aria-label="dwadzieścia osiem" role="math"><math><mn>28</mn></math></span>
| pole trapezu | |
| pole trójkąta |
Na czworokącie można opisać okrąg. Długości boków tego czworokąta są równe , , , a kąt ma miarę . Oblicz pole czworokąta .
W okrąg o średnicy wpisano trapez równoramienny w ten sposób, że suma kwadratów długości jego podstaw jest równa , a sinus kąta ostrego wynosi . Oblicz pole tego trapezu.