Sprawdź się

Pokaż ćwiczenia:

RlWwWOCu0v8TR1

Ćwiczenie 1

Rozważmy ostrosłup

A B C D S

, którego podstawą jest prostokąt

A B C D

. Krawędź boczna

S D

jest wysokością ostrosłupa, ponadto

|A S| = 10

|B S| = 2 \sqrt{41}

|C S| = 8 \sqrt{2}

. Połącz w pary wielkości z ich wartościami. długość przekątnej podstawy Możliwe odpowiedzi: 1.

0, 8

, 2.

10

, 3.

48

, 4.

96 + 24 \sqrt{2}

pole podstawy Możliwe odpowiedzi: 1.

0, 8

, 2.

10

, 3.

48

, 4.

96 + 24 \sqrt{2}

pole powierzchni bocznej Możliwe odpowiedzi: 1.

0, 8

, 2.

10

, 3.

48

, 4.

96 + 24 \sqrt{2}

tangens kąta nachylenia najdłuższej krawędzi bocznej do płaszczyzny podstawy Możliwe odpowiedzi: 1.

0, 8

, 2.

10

, 3.

48

, 4.

96 + 24 \sqrt{2}

Rozważmy ostrosłup $A B C D S$ , którego podstawą jest prostokąt $A B C D$ . Krawędź boczna $S D$ jest wysokością ostrosłupa, ponadto $"|"A S"|" = 10$ , $"|"B S"|" = 2 \sqrt{41}$ , $"|"C S"|" = 8 \sqrt{2}$ . Połącz wielkości z ich wartościami.

długość przekątnej podstawy
pole podstawy
pole powierzchni bocznej
tangens kąta nachylenia najdłuższej krawędzi bocznej do płaszczyzny podstawy

RKs7BIZeTVDhL1

Ćwiczenie 2

Dostępne opcje do wyboru:

\frac{s^{2} \sqrt{7}}{2}

2 s

\frac{s^{2}}{2}

\frac{1}{2} s

\frac{s^{2} \sqrt{3}}{2}

s^{2}

. Polecenie: Podstawą ostrosłupa jest romb o boku długości

s

i kącie ostrym

60 °

. Kąt pomiędzy równymi krawędziami bocznymi połączonymi dłuższą przekątną rombu ma miarę

120 °

.
Uzupełnij zdania, przeciągając prawidłowe odpowiedzi w puste miejsca.

Wysokość ostrosłupa ma długość luka do uzupełnienia .
Pole podstawy jest równe luka do uzupełnienia .
Pole powierzchni bocznej wynosi luka do uzupełnienia .

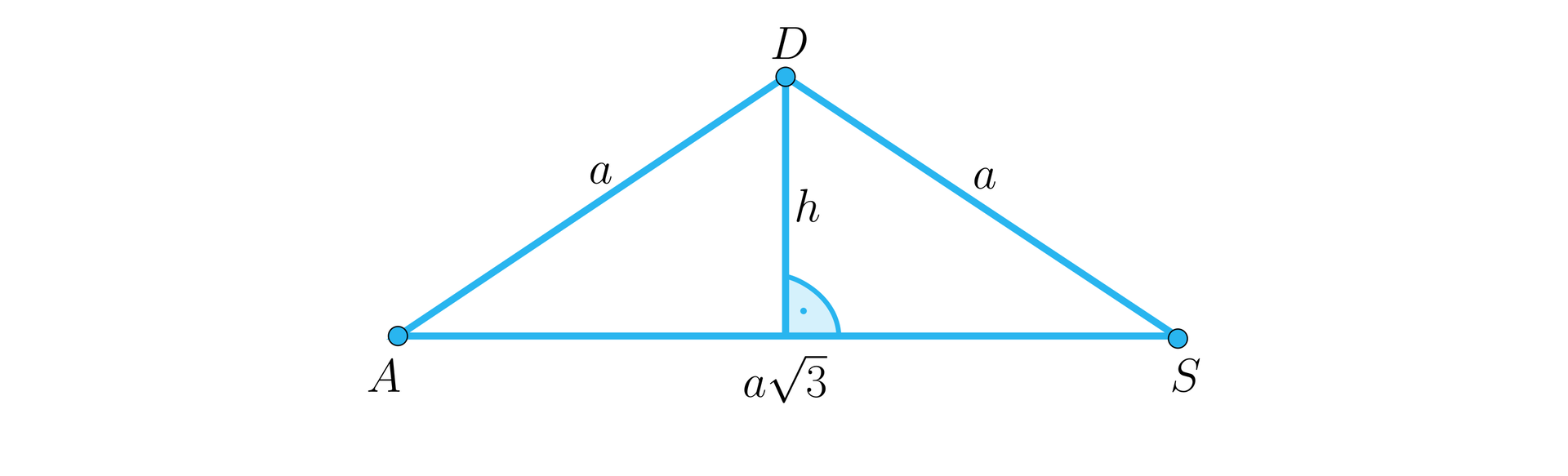
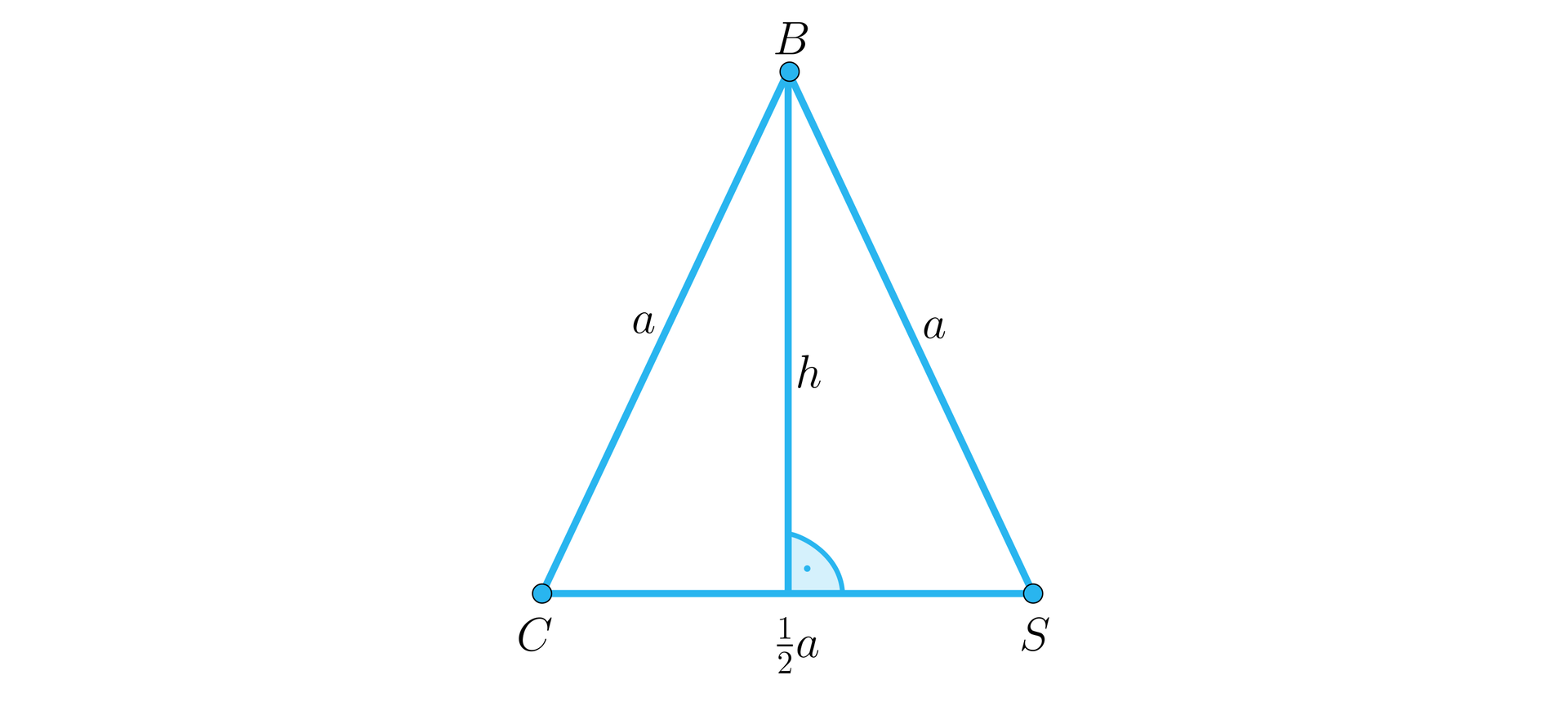
Podstawą ostrosłupa jest romb o boku długości $s$ i kącie ostrym $60 °$ . Kąt pomiędzy równymi krawędziami bocznymi połączonymi dłuższą przekątną rombu ma miarę $120 °$ .
Uzupełnij zdania, przeciągając prawidłowe odpowiedzi w puste miejsca.

$\frac{s^{2}}{2}$ , $2 s$ , $\frac{s^{2} \sqrt{3}}{2}$ , $\frac{s^{2} \sqrt{7}}{2}$ , $\frac{1}{2} s$ , $s^{2}$

Wysokość ostrosłupa ma długość .
Pole podstawy jest równe .
Pole powierzchni bocznej wynosi .

Ćwiczenie 3

Na rysunku przedstawiono siatkę ostrosłupa, którego podstawą jest kwadrat o boku długości $a$ . Wszystkie ściany boczne są trójkątami prostokątnymi.

R8XGVUuJIFlkB

Siatka ostrosłupa składa się z kwadratu o boku a oraz z czterech prostokątów o przyprostokątnych a oraz 2 a. Trójkąty są osadzone na bokach kwadratu.

R1U7HX2ydi1DH

R6G3fkLBvXpxQ2

Ćwiczenie 4

Podstawą ostrosłupa prostego $A B C D S$ jest trapez $A B C D$ . Przekątna $A C$ tego trapezu ma długość $12 \sqrt{3}$ , jest prostopadła do ramienia $B C$ i tworzy z dłuższą podstawą tego trapezu kąt o mierze $30 °$ . Każda krawędź boczna tego ostrosłupa ma długość $16$ .
Pole powierzchni bocznej ostrosłupa wynosi:

$48 \sqrt{55}$
$192 \sqrt{7}$
$36 \sqrt{55} + 48 \sqrt{7}$

Ćwiczenie 5

Na rysunku przedstawiono ostrosłup prosty o podstawie prostokąta, którego długości boków pozostają w stosunku $4 : 1$ . Punkty $E$ i $F$ są środkami przeciwległych krawędzi podstawy. Pole przekroju przedstawionego na rysunku wynosi $S^{2} tg α$ , gdzie $α$ jest miarą kąta nachylenia ściany bocznej do płaszczyzny podstawy.

R1cCBYVjlC8vY

Ilustracja przedstawia ostrosłup prosty o podstawie prostokąta. Wierzchołki podstawy to A B C D, natomiast wierzchołek górny ostrosłupa to S. W podstawie liniami przerywanymi zaznaczono jej przekątne. W ostrosłupie narysowano jego wysokość. W ostrosłupie zaznaczono się trójkąt o wierzchołkach FES, przy czym punkt E znajduje się na środku krawędzi podstawy BC a punk F znajduje się na środku krawędzi podstawy AD. Kąt FES został podpisany literą alfa.

RtvQKgi3b76HV

R1Km3D3m3jTbn2

Ćwiczenie 6

Przekrój ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez jego wierzchołek i przekątną podstawy jest trójkątem równobocznym o polu $2 P^{2} \sqrt{3}$ .
Pole powierzchni całkowitej tego ostrosłupa wynosi:

$4 P^{2}$
$4 P^{2} (1 + \sqrt{7})$
$4 P^{2} \sqrt{7}$

Ćwiczenie 7

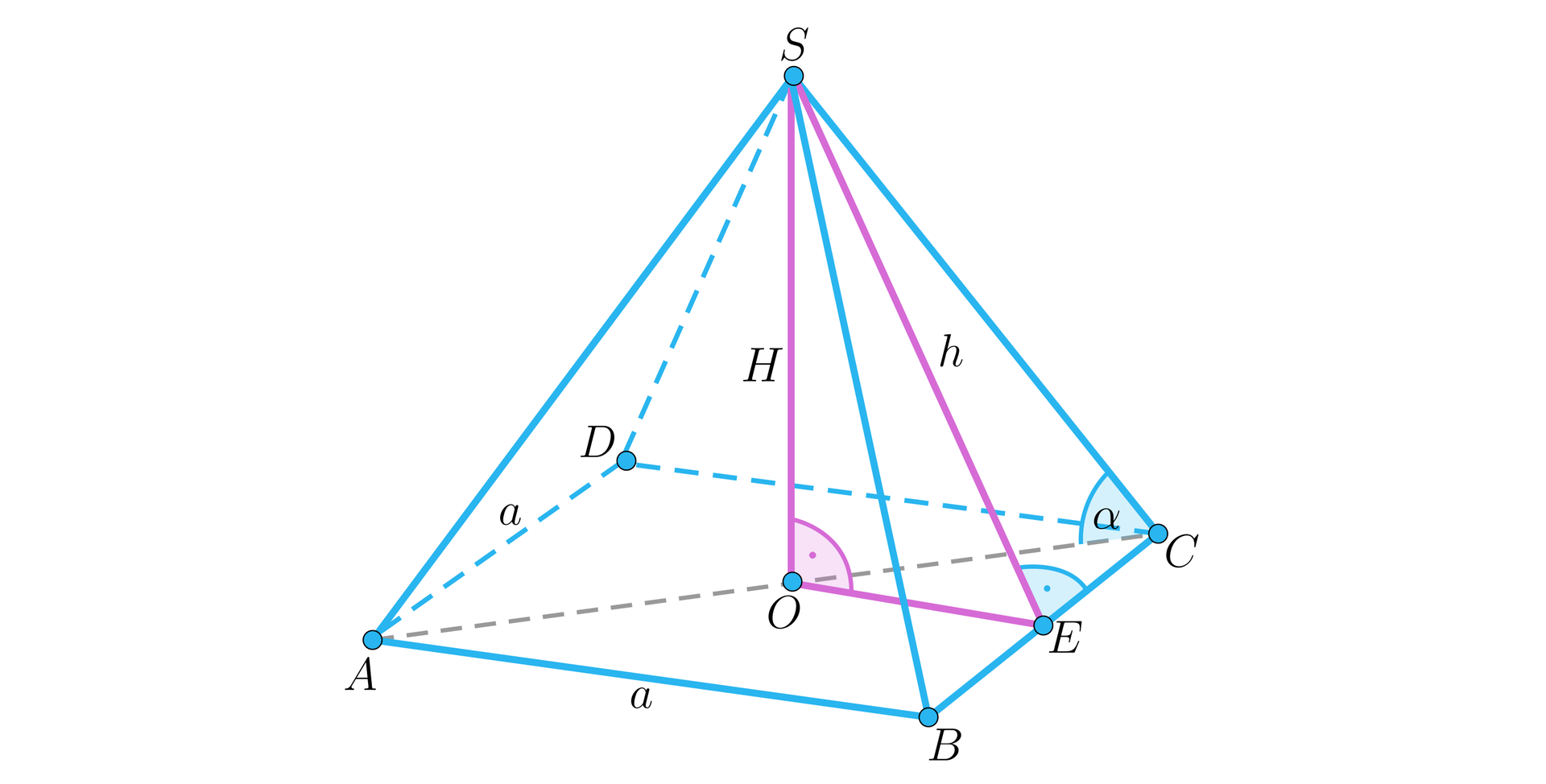
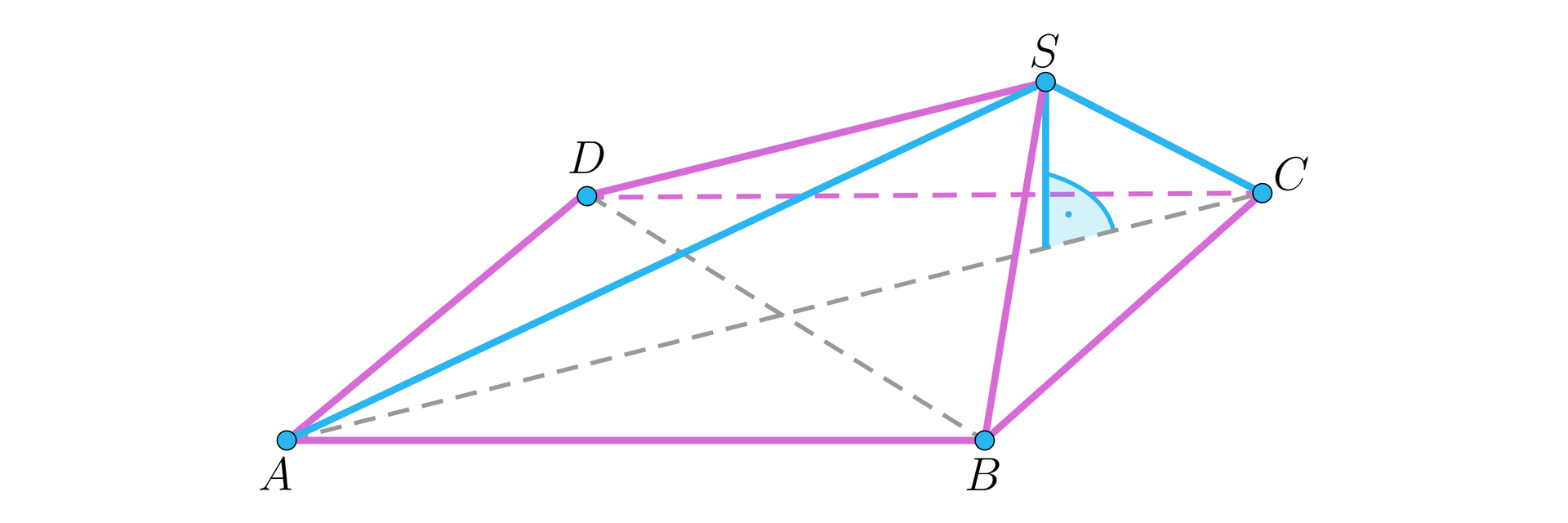
Wszystkie ściany boczne ostrosłupa o podstawie kwadratowej są trójkątami równoramiennymi (zobacz rysunek). Krawędzie, które są koloru różowego, mają taką samą długość równą $a$ . Oblicz pole powierzchni całkowitej tego ostrosłupa, wiedząc, że $\frac{|A D|}{|A S|} = \frac{\sqrt{3}}{3}$ oraz $\frac{|B C|}{|S C|} = 2$ .

R2qDzHQXrqBF8

Ilustracja przedstawia ostrosłup czworokątny, o wierzchołkach podstawy A B C D i wierzchołku górnym S. W podstawie liniami przerywanymi zaznaczono jej przekątne. W ostrosłupie zaznaczono jego wysokość opuszczoną na podstawę z wierzchołka S, spodek wysokości leży na przekątnej AC. Kolorem różowym zaznaczono krawędzie: AB, BC, CD, AD, BS oraz DS.

Z treści zadania wiemy, że

$\frac{|A D|}{|A S|} = \frac{\sqrt{3}}{3}$ , czyli $\frac{a}{|A S|} = \frac{\sqrt{3}}{3}$ , co daje, że $|A S| = a \sqrt{3}$

oraz

$\frac{|B C|}{|S C|} = 2$ , czyli $\frac{a}{|S C|} = 2$ , co daje, że $|S C| = \frac{1}{2} a$ .

Odcinek $A C$ jest przekątną kwadratu, zatem $|A C| = a \sqrt{2}$ .

Możemy zatem liczyć pole poszczególnych ścian naszego ostrosłupa:

$P_{p} = a^{2}$ .

Ściany boczne $D S A$ i $A S B$ są trójkątami przystającymi. Poprowadźmy wysokość z wierzchołka $D$ trójkąta $D S A$ . Oznaczmy ją jako $h$ .

R2ChHc1BonfPe

Ilustracja przedstawia trójkąt równoramienny o wierzchołkach ADS. Podstawa AS ma długość a3, ramiona AD oraz SD mają długość a. W ostrosłupie z wierzchołka D na podstawę AS opuszczono wysokość i podpisano ją literą h.

Wówczas:

$h^{2} = a^{2} - {(\frac{a \sqrt{3}}{2})}^{2}$

$h^{2} = a^{2} - \frac{3}{4} a^{2}$

$h^{2} = \frac{1}{4} a^{2}$

$h = \frac{1}{2} a$

$P_{A S D} = P_{A B S} = \frac{1}{2} \cdot a \sqrt{3} \cdot \frac{1}{2} a = \frac{a^{2} \sqrt{3}}{4}$ .

Zauważmy, że zamiast wyliczać wysokość, możemy skorzystać ze wzoru Herona. $P = \sqrt{{(\frac{a \sqrt{3}}{2})}^{2} \cdot (a + \frac{a \sqrt{3}}{2}) \cdot (a - \frac{a \sqrt{3}}{2})} = \sqrt{\frac{3 a^{2}}{4} \cdot \frac{a^{2}}{4}} = \frac{a^{2} \sqrt{3}}{4}$ .

Ściany boczne $D S C$ i $B S C$ są trójkątami przystającymi. Poprowadźmy wysokość z wierzchołka $B$ trójkąta $B S C$ . Oznaczmy ją jako $h$ .

R1VukFluZiqCq

Ilustracja przedstawia trójkąt równoramienny o wierzchołkach CBS. Podstawa CS ma długość < 12a,ramiona CB oraz BS mają długość a. W ostrosłupie z wierzchołka B na podstawę CS opuszczono wysokość i podpisano ją literą h.

Wówczas:

$h^{2} = a^{2} - {(\frac{1}{4} a)}^{2}$

$h^{2} = a^{2} - \frac{1}{16} a^{2}$

$h^{2} = \frac{15}{16} a^{2}$

$h = \frac{\sqrt{15}}{4} a$

$P_{B S C} = P_{D S C} = \frac{1}{2} \cdot \frac{1}{2} a \cdot \frac{\sqrt{15}}{4} a = \frac{a^{2} \sqrt{15}}{16}$ .

Korzystając ze wzoru Herona otrzymujemy: $P = \sqrt{\frac{5}{4} a \cdot \frac{1}{4} a \cdot \frac{1}{4} a \cdot \frac{3}{4} a} = a^{2} \frac{\sqrt{15}}{16}$ .

Zatem $P_{b} = 2 \cdot \frac{a^{2} \sqrt{3}}{4} + 2 \cdot \frac{a^{2} \sqrt{15}}{16} = \frac{a^{2} \sqrt{3}}{2} + \frac{a^{2} \sqrt{15}}{8}$

$P_{c} = a^{2} + \frac{a^{2} \sqrt{3}}{2} + \frac{a^{2} \sqrt{15}}{8} = a^{2} (1 + \frac{\sqrt{3}}{2} + \frac{\sqrt{15}}{8})$ .

Ćwiczenie 8

W ostrosłupie prawidłowym czworokątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem $α$ . Wykaż, że pole powierzchni bocznej ostrosłupa o wysokości równej $H$ wynosi $\frac{2 H^{2} \sqrt{2 {tg}^{2} α + 1}}{{tg}^{2} α}$ .

Wykonajmy rysunek pomocniczy. Wprowadźmy dodatkowe oznaczenia. Niech $a$ – długość krawędzi podstawy, $h$ – wysokość ściany bocznej ostrosłupa.

RQ4ZWXDiY2xGU

Ilustracja przedstawia ostrosłup prawidłowy czworokątny o wierzchołkach podstawy A B C D. Krawędź AD oraz AB podpisano literą H. Wierzchołek ostrosłupa podpisano literą S, z tego wierzchołka poprowadzono wysokość a jej spodek podpisano literą O, wysokość tą podpisano literą wielkie H. W trójkątnej ścianie bocznej BCS z wierzchołka S na krawędź BC opuszczono wysokość i podpisano ją małe h, której spodek podpisano literą E. Odcinki SO, SE oraz OE tworzą trójkąt prostokątny, w którym odcinek SE jest przeciwprostokątną. W podstawie zaznaczono jej przekątną AC, kąt pomiędzy tą przekątną a krawędzią boczną CS podpisano literą alfa.

Trójkąt $S O C$ jest prostokątny, zatem wykorzystując funkcję tangens mamy:

$tg α = \frac{H}{|O C|}$

$tg α = \frac{H}{\frac{a \sqrt{2}}{2}}$

$\frac{a \sqrt{2}}{2} = \frac{H}{tg α}$

$a = \frac{H \sqrt{2}}{tg α}$ .

Obliczmy wysokość ściany bocznej. Trójkąt $S O E$ jest prostokątny. Z twierdzenia Pitagorasa mamy więc:

$H^{2} + {(\frac{1}{2} a)}^{2} = h^{2}$

$H^{2} + {(\frac{H \sqrt{2}}{2 tg α})}^{2} = h^{2}$

$H^{2} + \frac{2 H^{2}}{4 {tg}^{2} α} = h^{2}$

$\frac{4 H^{2} {tg}^{2} α + 2 H^{2}}{4 {tg}^{2} α} = h^{2}$

$h = \sqrt{\frac{H^{2} (4 {tg}^{2} α + 2)}{4 {tg}^{2} α}}$

$h = \frac{H \sqrt{4 {tg}^{2} α + 2}}{2 tg α}$ .

Obliczmy więc pole powierzchni bocznej:

$P_{b} = 4 \cdot \frac{1}{2} \cdot a h = 2 \cdot \frac{H \sqrt{2}}{tg α} \cdot \frac{H \sqrt{4 {tg}^{2} α + 2}}{2 tg α} = \frac{H^{2} \sqrt{8 {tg}^{2} α + 4}}{{tg}^{2} α} = \frac{2 H^{2} \sqrt{2 {tg}^{2} α + 1}}{{tg}^{2} α}$ .

Animacja 3D

Dla nauczyciela