Sprawdź się

Pokaż ćwiczenia:

RVuIS1irWkPjB1

Ćwiczenie 1

Wskaż poprawną definicję siły odśrodkowej

pozorna siła występująca w obracającym się układzie nieinercjalnym, skierowana do środka okręgu
rzeczywista siła występująca w obracającym się układzie nieinercjalnym, skierowana od środka okręgu
pozorna siła występująca w obracającym się układzie nieinercjalnym, skierowana od środka okręgu
pozorna siła występująca w obracającym się układzie inercjalnym skierowana od środka okręgu

Rnyyh9HaiLAWg1

Ćwiczenie 2

Samochód o masie $M$ zaczyna poruszać się z przyspieszeniem $\vec{a}$ . Wektor przyspieszenia skierowany jest w prawo. Na dachu samochodu stoi kubek z kawą o masie $m$ , który nieuważny kierowca zapomniał zabrać do środka pojazdu. Jaka siła bezwładności będzie działać na kubek w nieinercjalnym układzie związanym z samochodem?

$F_{b} = M a$ , skierowana w lewo
$F_{b} = m a$ , skierowana w lewo
$F_{b} = M a$ , skierowana w prawo
$F_{b} = m a$ , skierowana w prawo

R1CNbmLjgjCK41

Ćwiczenie 3

Zaznacz wszystkie sytuacje, w których na danego obserwatora (wyszczególnionego w konkretnej sytuacji) będzie działać siła bezwładności.

maszynista pociągu rozpędza pojazd na prostym odcinku torów
pies wraz ze swoim opiekunem przechodzą ze stałą szybkością przez przejście dla pieszych i obserwują hamujące przed nimi samochody
dziewczynka siedzi na rozpędzającej się karuzeli
poruszający się ze stałą szybkością rowerzysta wchodzi w zakręt

R1Ud3XeDCUzWw1

Ćwiczenie 4

Przyporządkuj siły bezwładności odpowiednim sytuacjom, w których występują.

odczuwa siłę skierowaną do zewnętrznego brzegu fotela, odczuwa siłę wypychającą go z fotela, odczuwa siłę wpychającą go w fotel, odczuwa siłę wpychającą go w podłoże

Pasażer rozpędzającego się samolotu
Kierowca gwałtownie hamującego samochodu
Dziewczynka siedząca na fotelu wirującej karuzeli
Użytkownik wagonika kolejki na „diabelskiej pętli” znajdujący się w najniższym punkcie toru

R1596q4xsWbQO

Ćwiczenie 4

Ćwiczenie 5

R3DuvbeN9oPm5

Zaczepiony na nitce o długości

l

= 25 cm ciężarek wiruje z ustaloną częstotliwością w płaszczyźnie pionowej. Jaka to częstotliwość, jeżeli wartość siły odśrodkowej w najwyższym punkcie toru jest trzy razy większa od siły wypadkowego naciągu nici? Przyjmij wartość

g

= 9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących. Odpowiedź:

f

= Tu uzupełnij Hz

Zaczepiony na nitce o długości $l$ = 25 cm ciężarek wiruje z ustaloną częstotliwością w płaszczyźnie pionowej. Jaka to częstotliwość, jeżeli wartość siły odśrodkowej w najwyższym punkcie toru jest trzy razy większa od siły wypadkowego naciągu nici? Przyjmij wartość $g$ = 9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących.

Odpowiedź: $f$ = ............ Hz.

W układzie nieinercjalnym na ciężarek w jego najwyższym położeniu działają dwie siły - skierowana do góry siła odśrodkowa o wartości $F_o=m\omega^2 l$ i skierowana do dołu siła grawitacji $F_g=mg$ . Wypadkowa siła działająca na ciężarek w tym układzie jest równa $F_w=m\omega^2 l - mg$ . Siła naciągu nici w układzie inercjalnym jest co do wartości równa $|F_N|=|F_w|$ . Naciąg nici w najwyższym punkcie wynosi zatem $F_N=m\omega^2 l - mg$ .

Siła odśrodkowa $F_o=m\omega^2 l$ jest trzykrotnie większa niż wypadkowy naciąg nici $F_N=m\omega^2 l - mg$ . Zatem

$m\omega^2 l=3(m\omega^2 l - mg)$ .

Po przekształceniach

$\omega=\sqrt{\frac{3g}{2l}}$

oraz

$f=\frac{1}{2\pi}\sqrt{\frac{3g}{2l}}=\frac{1}{2\cdot 3,14}\sqrt{\frac{3\cdot 9,81}{2\cdot 0,5}} Hz\approx 1,22 Hz.$

Ćwiczenie 6

R1O1gHXSFohKT

Z jaką minimalną prędkością należy kręcić wiadrem zawierającym wodę umieszczonym na lince o długości $l$ = 40 cm, aby w najwyższym punkcie toru woda nie wylewała się z wiadra? Przyjmij wartość $g$ = 9,81 m/s², a wynik podaj z dokładnością do dwóch cyfr znaczących.

Odpowiedź: $v_{min}$ = ............ m/s.

W układzie nieinercjalnym, w najwyższym puncie toru na wodę w wiadrze działają trzy siły: siła ciężkości $\vec{F_g}$ , siła odśrodkowa $\vec{F_c}$ oraz siła reakcji dna wiadra $\vec{F_r}$ . Założenie, że woda nie wylewa się z wiadra oznacza, że wypadkowa tych sił musi być równa zero:

$\vec{F_g}+\vec{F_o}+\vec{F_r}=\vec{0}.$

W zapisanie skalarnym równanie to ma postać:

$F_g-F_o+F_r=0.$

Wiedząc, że wartość siły reakcji nie może być mniejsza od zera dostajemy nierówność

$F_o\ge F_g,$

z której można wyznaczyć minimalną wartość prędkość wiadra.

Porównując wartości siły odśrodkowej $F_o=\frac{mv^2}{l}$ i siły ciężkości $F_g=mg$ dostajemy:

$\frac{mv^2}{l}\ge mg$ .

Zatem

$v_{\text{min}}=\sqrt{gl}=\sqrt{9,81\cdot0,4}\frac{m}{s}\approx2,0\frac{m}{s}.$

Ćwiczenie 7

R4PQMQ6O39IOp

Samochód porusza się po zakręcie o promieniu

R

= 250 m, który wyprofilowany został pod kątem 15° do poziomu. Załóżmy dodatkowo, że tarcie można zaniedbać (powierzchnia drogi jest oblodzona). Z jaką maksymalną prędkością może poruszać się samochód, by nie wypaść z zakrętu? Przyjmij wartość

g

= 9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących. Odpowiedź:

v

= Tu uzupełnij m/s

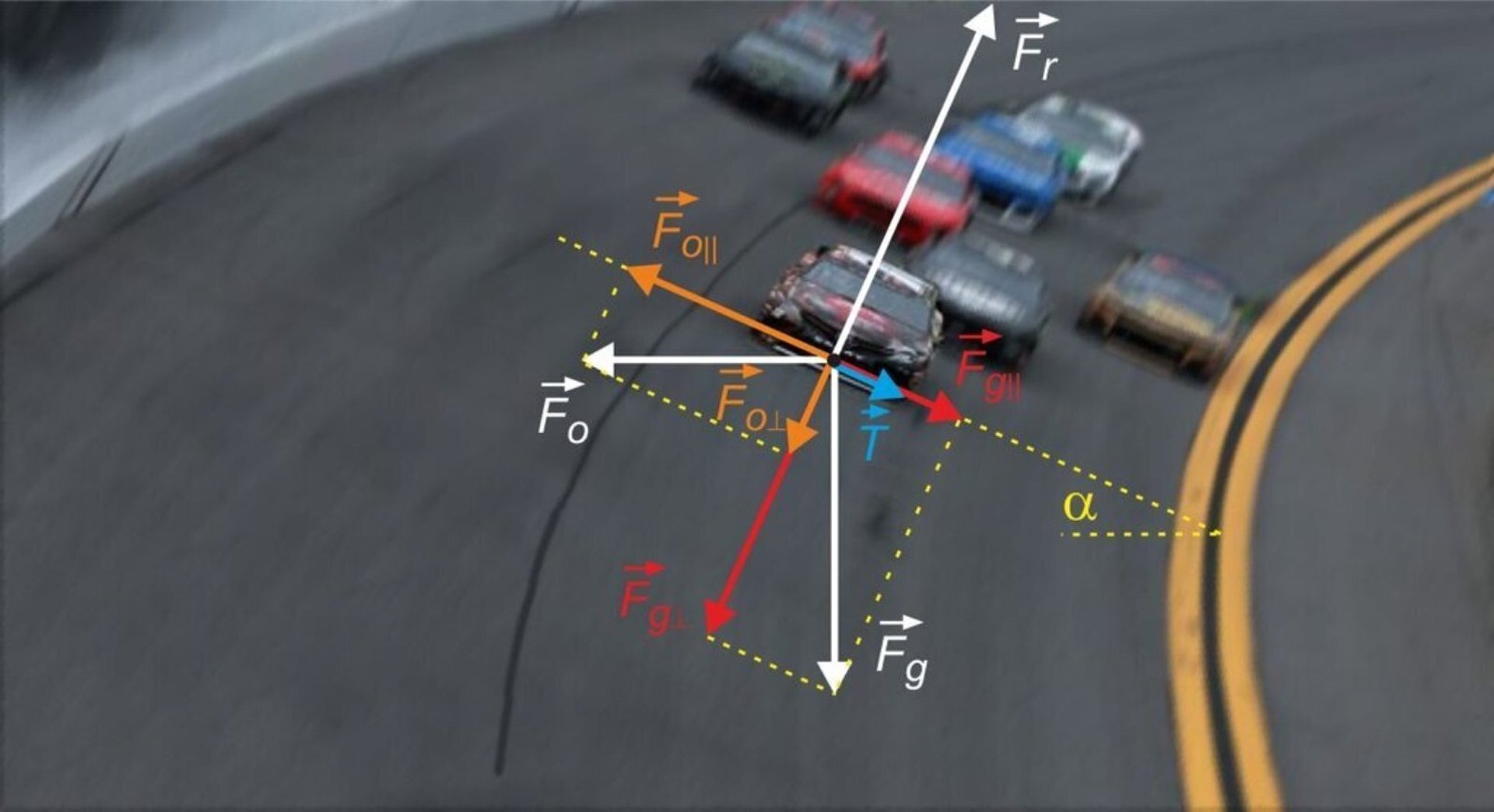
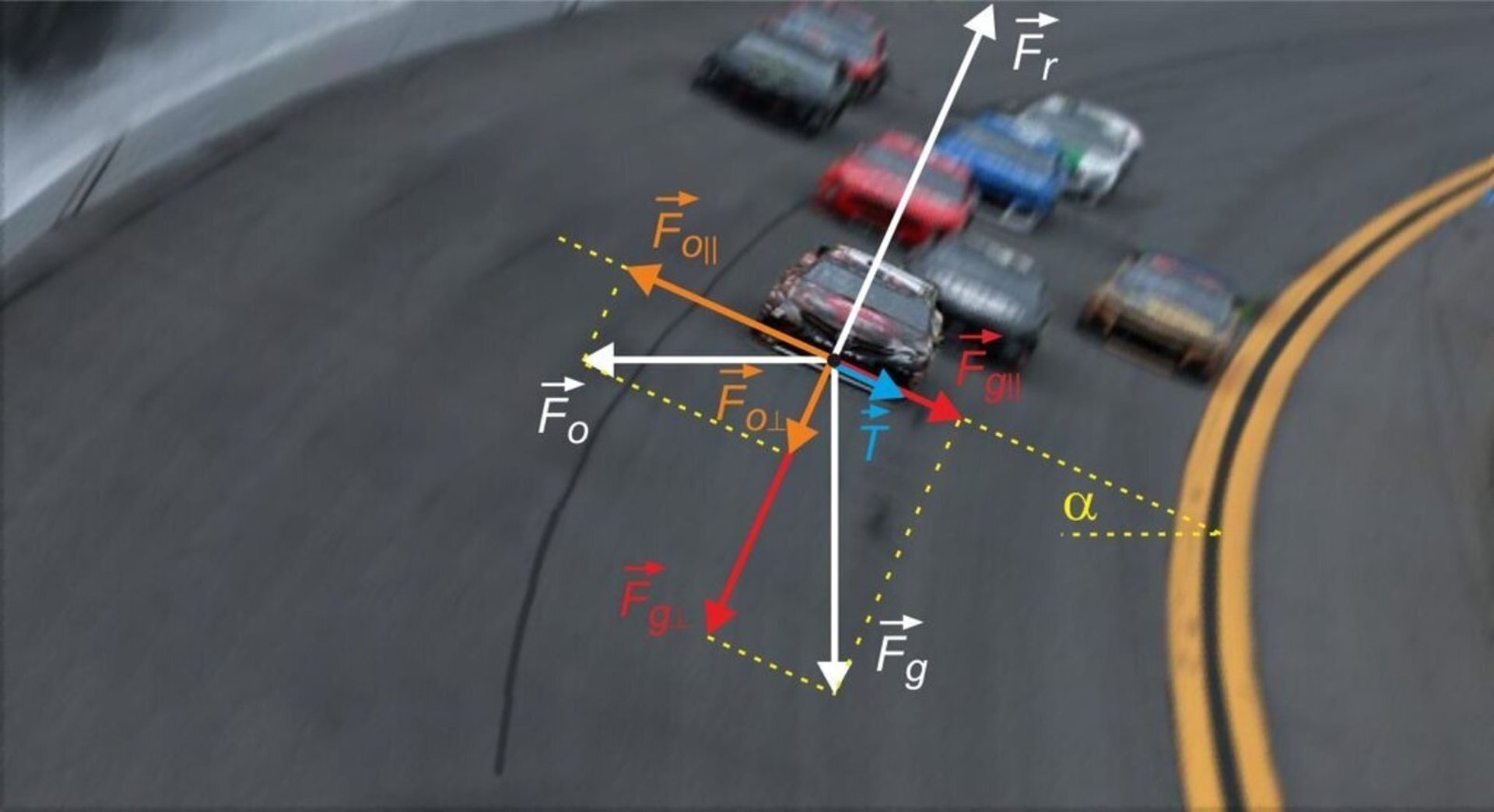
Samochód porusza się po zakręcie o promieniu R=250 m, który wyprofilowany został pod kątem α=15° do poziomu. Droga jest oblodzona, więc tarcie trzeba zaniedbać. Z jaką prędkością powinien się poruszać ten samochód, by nie wypaść z zakrętu? Przyjmij wartość g=9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących.

Odpowiedź: $v$ = ............ m/s = ............ km/h.

W układzie nieinercjalnym na samochód działają trzy siły: siła grawitacji $\vec{F_g}$ , siła odśrodkowa $\vec{F_o}$ i siła reakcji (sprężystości) od podłoża $\vec{F_r}$ . Jeśli samochód ma się poruszać się ze stałą prędkością wówczas, zgodnie z pierwszą zasada dynamiki, siły te muszą się równoważyć. W szczególności, muszą się one równoważyć w kierunku równoległym do powierzchni drogi, czyli $F_{g_{||}}=F_{o_{||}}$ (zob. Rys.).

RDuhW8F0skgf7

Rysunek przedstawia tor wyścigowy po którym poruszają się samochody rajdowe oraz rozkład sił działających na te samochody. Tor jest wyprofilowany i lekko pochylony ku środkowi na zakręcie. Na środek ciężkości samochodu działają siły. Siła ciężkości, siła odśrodkowa i siła sprężystości. Każdą z nich rozłożono na składowe prostopadłe i równoległe do powierzchni toru. — Źródło: Politechnika Warszawska, Wydział Fizyki, licencja: CC BY 4.0. https://creativecommons.org/licenses/by/4.0/deed.pl.

Składowa siły odśrodkowej równoległa do płaszczyzny drogi $F_{o_{||}}=\frac{mv^2}{R}\cos(15^{\circ})$ oraz składowa siły grawitacji $F_{g_{||}}=mg\sin(15^{\circ})$ muszą się równoważyć. Zatem

$\frac{mv^2}{R}\cos(15^{\circ})=mg\sin(15^{\circ}),$

czyli wartość prędkości samochodu musi być równa:

$v=\sqrt{g\cdot R\cdot\text{tg}(15^{\circ})}=\sqrt{9,81\frac{\text{m}}{\text{s}^2}\cdot250\text{ m}\cdot0,268}\approx25,6\frac{\text{m}}{\text{s}}$ .

Ćwiczenie 8

RL0zUjrTzAqzT

Samochód porusza się z po zakręcie o promieniu

R

= 450 m z prędkością

v

= 108 km/h. Zakręt jest wyprofilowany pod kątem 8° do poziomu. W pewnym momencie samochód wjeżdża w kałużę, w wyniku czego współczynnik tarcia kół o podłoże maleje do

f

= 0,02. Czy samochód utrzyma się na zakręcie? Podaj maksymalną bezpieczną prędkość samochodu dla takich parametrów zakrętu oraz wartości współczynnika tarcia. Przyjmij wartość

g

= 9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących. Odpowiedź: Samochód nie utrzyma się na zakręcie,

v_{m a x}

= Tu uzupełnij m/s.

Samochód porusza się po zakręcie o promieniu R=450 m z prędkością v=108 km/h. Zakręt jest wyprofilowany pod kątem α=8° do poziomu. W pewnym momencie samochód wjeżdża w kałużę, w wyniku czego współczynnik tarcia kół o podłoże maleje do f=0,02. Czy samochód utrzyma się na zakręcie? Podaj maksymalną bezpieczną prędkość samochodu dla takich parametrów zakrętu oraz wartości współczynnika tarcia. Przyjmij wartość g=9,81 m/s², a wynik podaj z dokładnością do trzech miejsc znaczących.

Odpowiedź:
Samochód nie utrzyma się na zakręcie.
Maksymalna bezpieczna szybkość wynosi: $v_{m a x}$ = ............ m/s= ............ km/h.

Rz77X7BYAns5j

W układzie nieinercjalnym, w płaszczyźnie poprzecznej do kierunku ruchu, na samochód działają cztery siły (zob. Rys.): siła grawitacji $\vec{F_g}$ , siła odśrodkowa $\vec{F_o}$ , siła reakcji (sprężystości) od podłoża $\vec{F_r}$ oraz siła tarcia statycznego kół samochodu o podłoże $\vec{T.}$ Samochód wypadnie z zakrętu, gdy w kierunku poprzecznym do ruchu nastąpi zerwanie tarcia statycznego. Stanie się tak wtedy, gdy różnica wartości $F_{o_{||}}-F_{g_{||}}$ składowych sił odśrodkowej $\vec{F_{o_{||}}}$ i grawitacji $\vec{F_{g_{||}}}$ , które są równoległe do nawierzchni, przekroczy wartość maksymalnej siły tarcia statycznego, o wartości $T_{\text{max}}=f\cdot F_r,$ gdzie $F_r=F_{g_{\perp}}+F_{o_{\perp}}$ .

Zgodnie z tym, co napisano w podpowiedzi, wyrażenie, z którego można wyznaczyć maksymalną bezpieczną prędkość samochodu ma postać:

$F_{o_{||}}-F_{g_{||}}\le T_{\text{max}},$

skąd po podstawieniu odpowiednich wzorów dostajemy:

$\frac{mv^2}{R}\cos(\alpha)-mg\sin(\alpha)\le f\cdot\left(\frac{mv^2}{R}\sin(\alpha)+mg\cos(\alpha)\right).$

Po przekształceniu powyższej zależności mamy:

$v_{\text{max}}=\sqrt{gR\frac{\sin\alpha+f\cos\alpha}{\cos\alpha-f\sin\alpha}}=\dots\approx26,7\frac{\text{m}}{\text{s}}.$

Symulacja interaktywna

Dla nauczyciela