Sprawdź się
Pokaż ćwiczenia:
Ćwiczenie 1
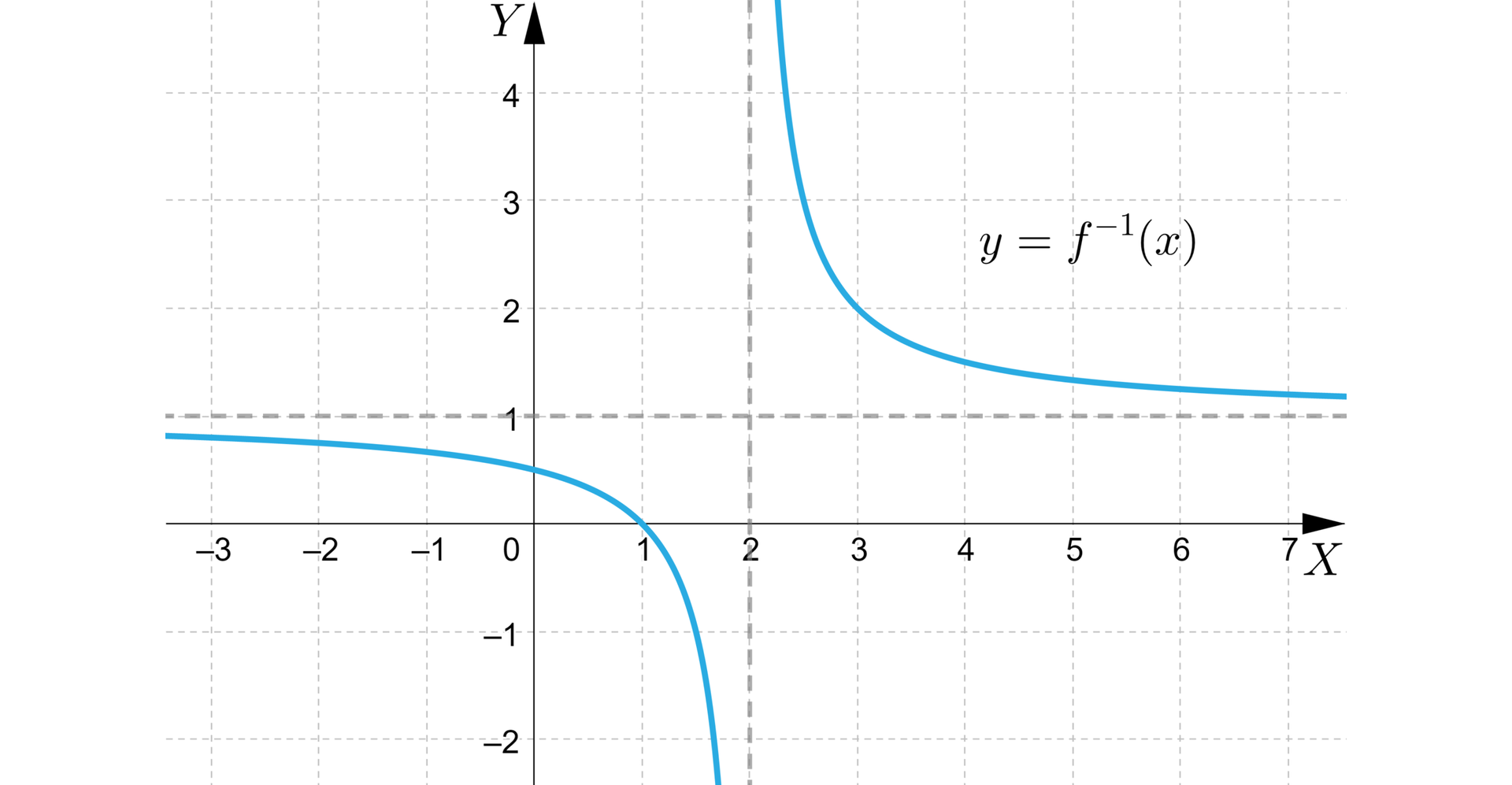
Dana jest funkcja homograficzna. Jest to bijekcja, posiada funkcję odwrotną. Czy punkt o współrzędnych należy do wykresu funkcji odwrotnej do funkcji, której wykres przedstawiony jest na rysunku?

Ćwiczenie 2
- Wykres funkcji składa się z dwóch ćwiartek różnych okręgów. Lewa część wykresu to dolna prawa ćwiartka okręgu jednostkowego o środku w punkcie o współrzędnych . Lewy koniec łuku o współrzędnych jest oznaczony zamalowanym punktem, a z prawej strony łuk ograniczony jest niezamalowanym punktem o współrzędnych . Łuk ten leży w trzeciej ćwiartce układu współrzędnych. Prawa część wykresu to lewa górna ćwiartka okręgu jednostkowego o środku w punkcie o współrzędnych . Znajduje się ona w pierwszej ćwiartce układu współrzędnych. Funkcja :
posiada funkcję odwrotną,
nie podsiada funkcji odwrotnej. - Wykres funkcji składa się z dwóch ćwiartek okręgu o środku w punkcie , które leżą w drugiej i w pierwszej ćwiartce układu współrzędnych, czyli wykresem jest górny półokrąg. Funkcja :
posiada funkcję odwrotną,
nie podsiada funkcji odwrotnej. - Wykres funkcji składa się z dwóch ćwiartek różnych okręgów. Lewa część wykresu to dolna prawa ćwiartka okręgu jednostkowego o środku w punkcie o współrzędnych . Oba końce łuku są oznaczone zamalowanymi punktami. Łuk ten leży w trzeciej ćwiartce układu współrzędnych. Prawa część wykresu to lewa górna ćwiartka okręgu jednostkowego o środku w punkcie o współrzędnych . Znajduje się ona w pierwszej ćwiartce układu współrzędnych. Funkcja :
posiada funkcję odwrotną,
nie podsiada funkcji odwrotnej.
Ćwiczenie 3
Ćwiczenie 4
Ćwiczenie 5
Dana jest funkcja homograficzna . Wyznacz funkcję do niej odwrotną.
Naszkicuj jej wykres.
Opisz jej wykres.
Ćwiczenie 6
Dana jest funkcja . Wyznacz funkcję odwrotną do niej.
Naszkicuj jej wykres.
Opisz jej wykres.
Ćwiczenie 7
Wyznacz funkcję odwrotną do , .
Ćwiczenie 8
Wyznacz (jeżeli istnieje) funkcję odwrotną do funkcji , określonej wzorem: .