Sprawdź się
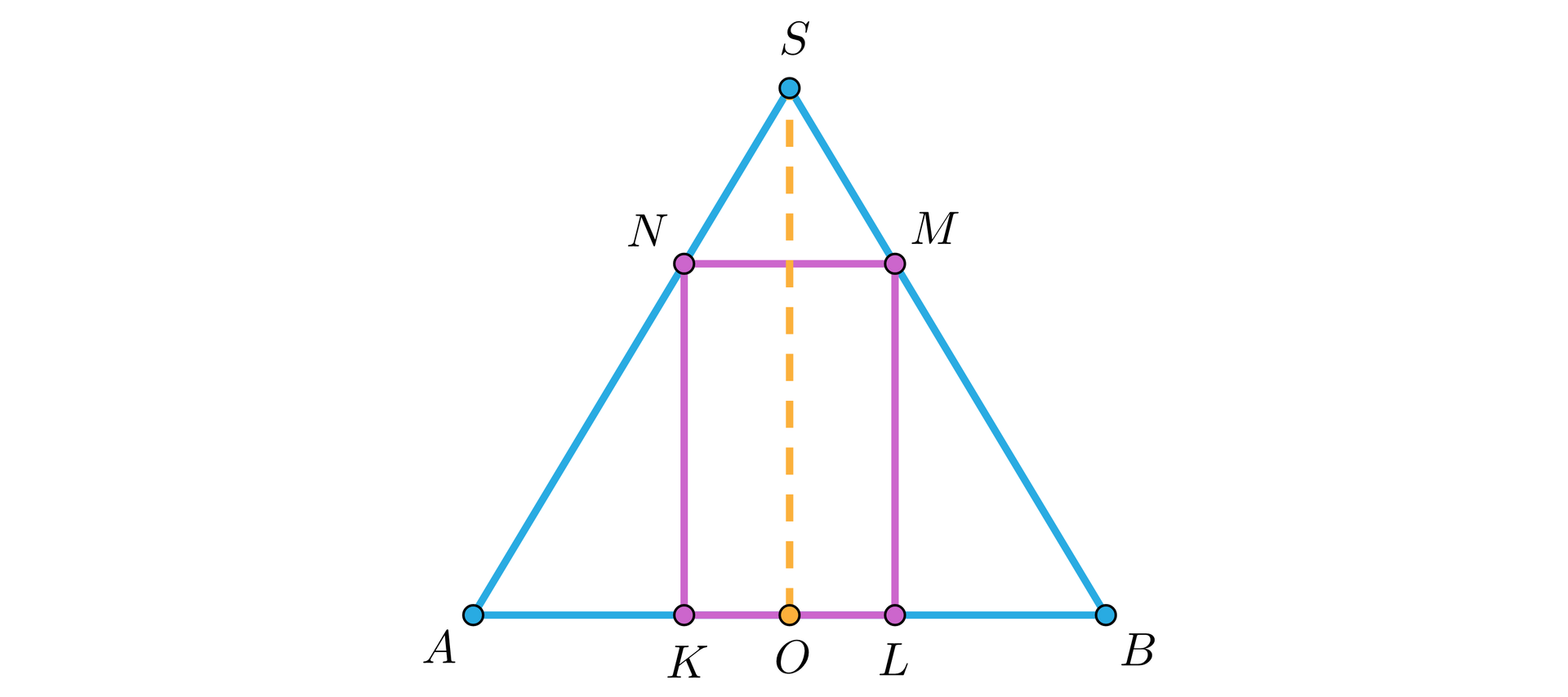
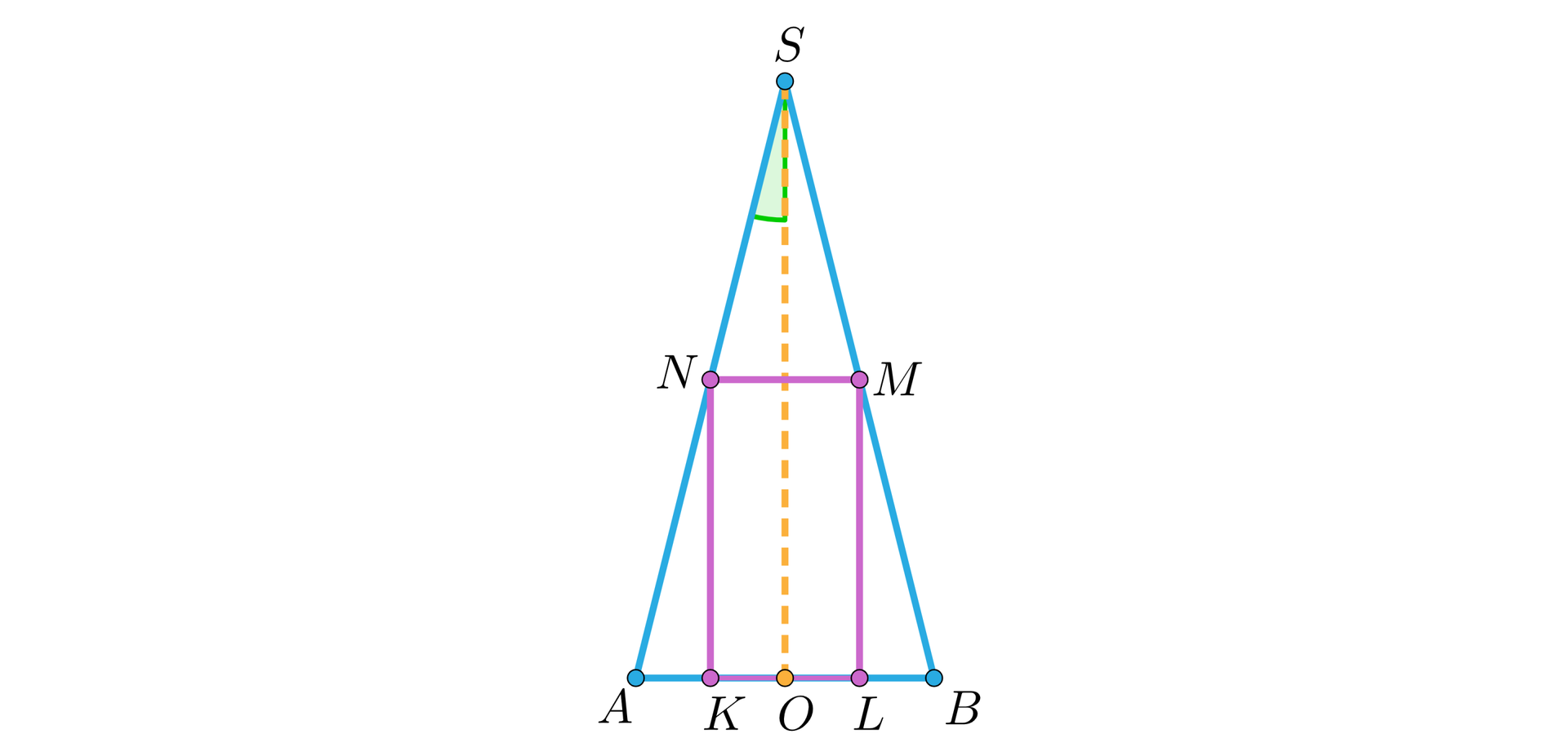
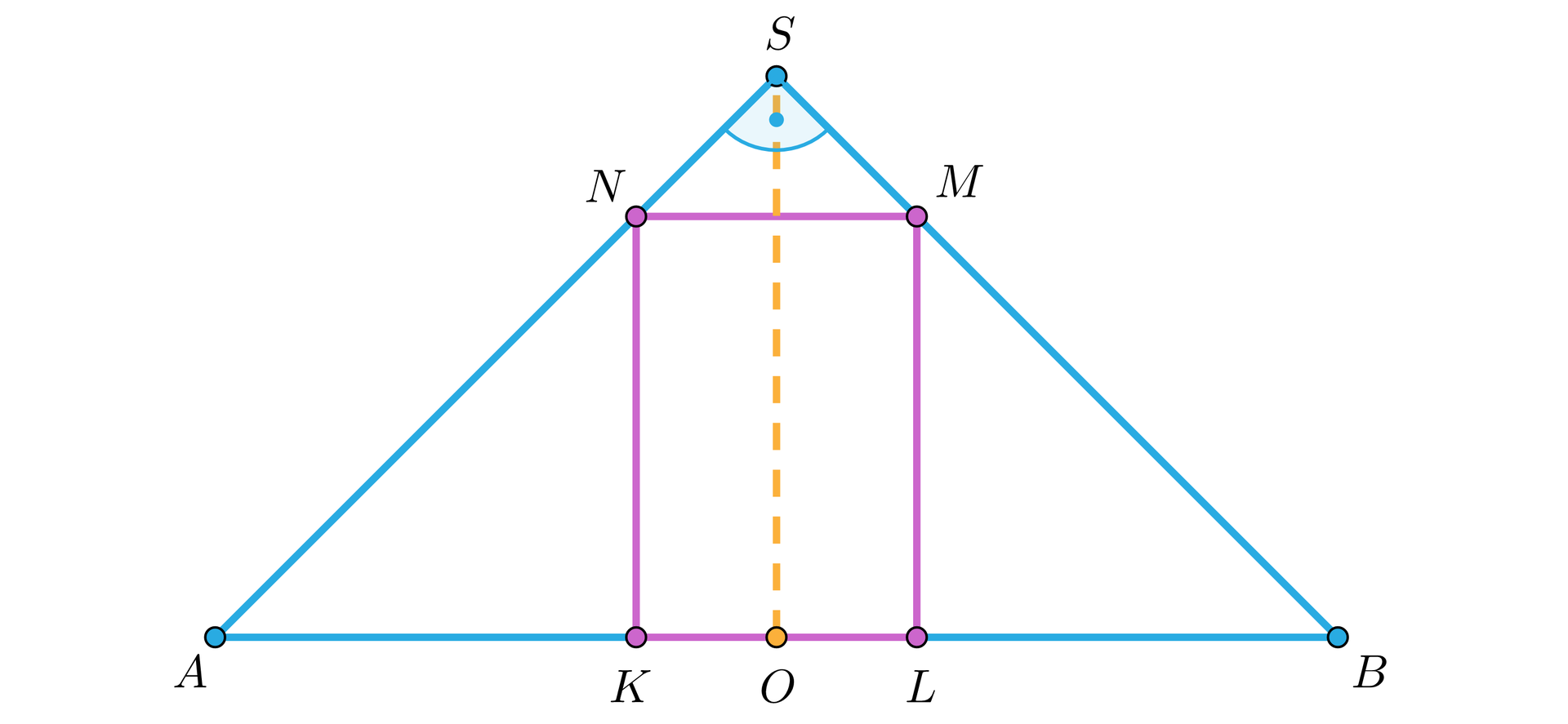
Na rysunku wykreślono przekrój osiowy walca wpisanego w stożek. Zaznacz wszystkie zależności, które są prawdziwe.
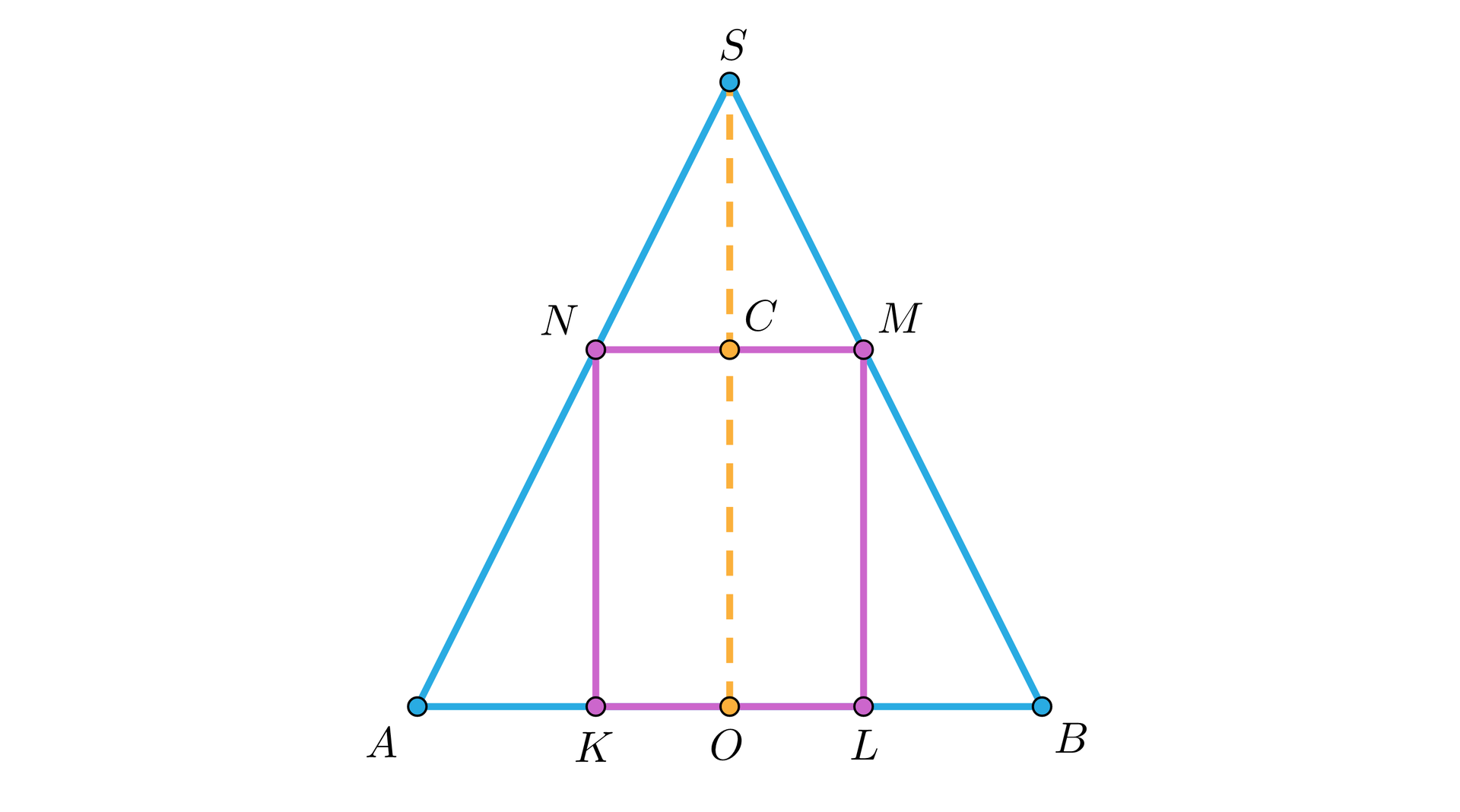
Na rysunku wykreślono przekrój osiowy walca wpisanego w stożek. Długość promienia podstawy walca wynosi , a długość jego wysokości . Długość promienia podstawy stożka wynosi . Oblicz, ile centymetrów ma wysokość stożka. Zakoduj odpowiedni cyfrę setek, dziesiątek i jedności uzyskanego wyniku (wpisz w pola tekstowe).
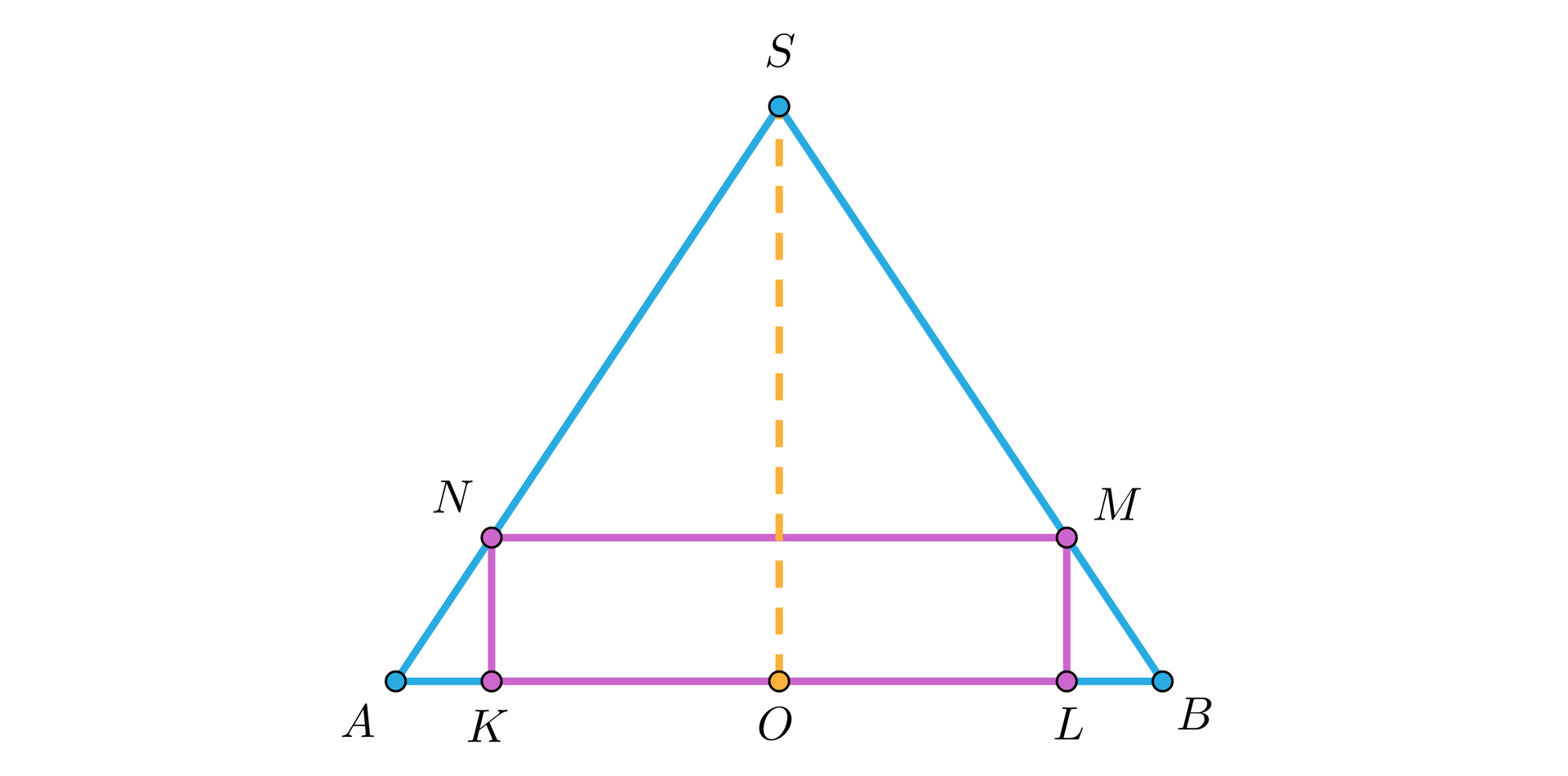
Rozważmy stożek o promieniu podstawy długości i wysokości długości . W stożek ten wpisano walec o promieniu podstawy długości . Oblicz pole powierzchni całkowitej tego walca.
W stożek wpisano walec. Długość wysokości walca jest dwa razy większa od długości promienia podstawy stożka. Stosunek pola powierzchni całkowitej walca do pola powierzchni podstawy stożka wynosi . Wyznacz tangens kąta zawartego pomiędzy wysokością stożka a jego tworzącą.
Kąt rozwarcia stożka ma miarę , a jego tworząca ma długość . W stożek ten wpisano walec, taki, że stosunek długości wysokości walca do długości promienia podstawy walca wynosi . Oblicz objętość walca.
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości . W stożek ten wpisano walec taki, że stosunek długości wysokości walca do długości promienia podstawy walca wynosi . Oblicz długość promienia podstawy walca.