Sprawdź się
Niech będzie promieniem okręgu wpisanego w trójkąt (oznaczenia boków i wysokości standardowe). Przyporządkuj wzór na promień okręgu wpisanego do rodzaju trójkąta:
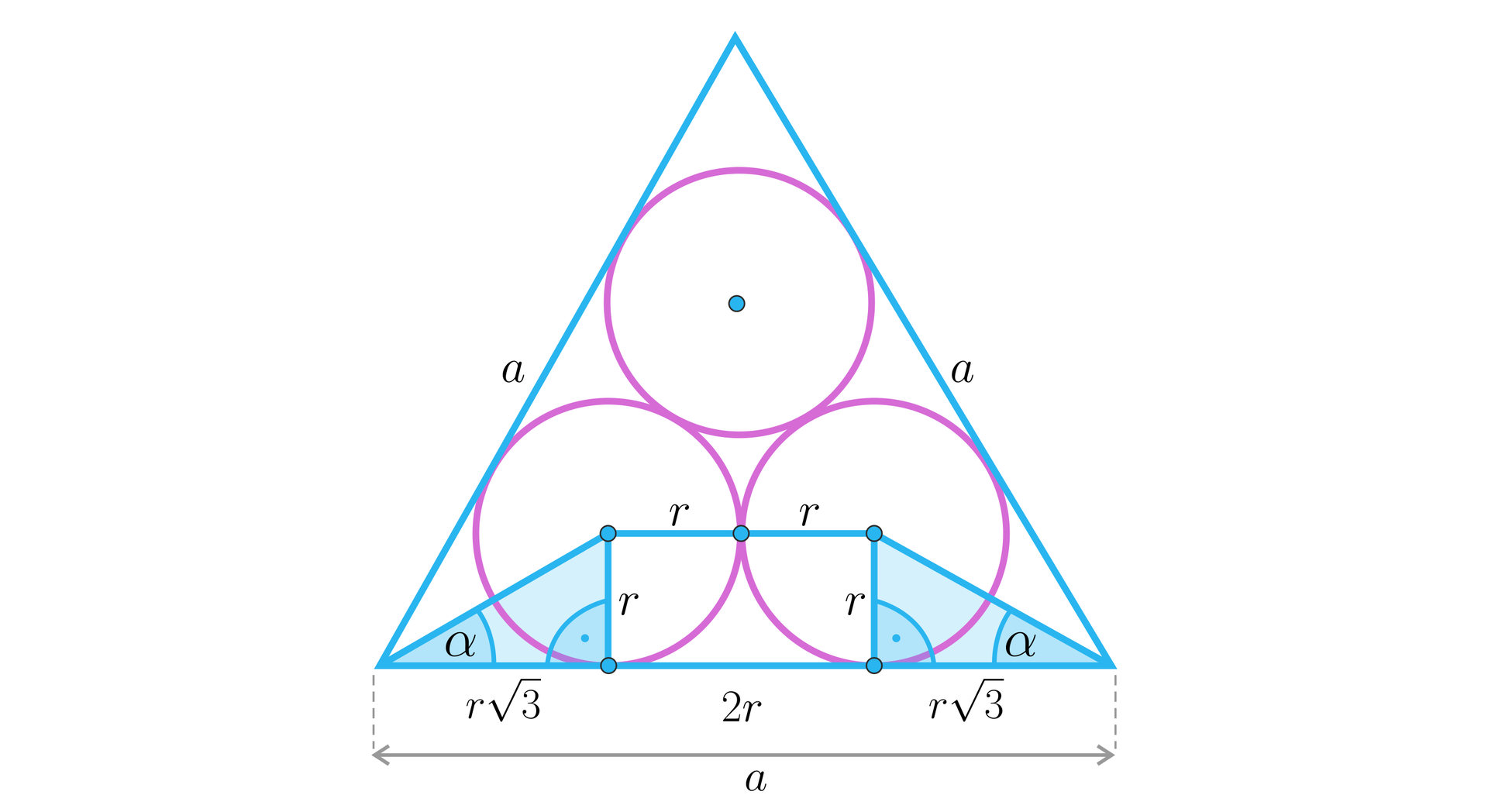
<span aria-label="r, równa się, początek ułamka, a, plus, b, minus, c, mianownik, dwa, koniec ułamka" role="math"><math><mi>r</mi><mo>=</mo><mfrac><mrow><mi>a</mi><mo>+</mo><mi>b</mi><mo>-</mo><mi>c</mi></mrow><mn>2</mn></mfrac></math></span>, <span aria-label="r, równa się, początek ułamka, a pierwiastek kwadratowy z trzy, mianownik, sześć, koniec ułamka" role="math"><math><mi>r</mi><mo>=</mo><mfrac><mrow><mi>a</mi><msqrt><mn>3</mn></msqrt></mrow><mn>6</mn></mfrac></math></span>, <span aria-label="r, równa się, początek ułamka, a h, mianownik, a, plus, dwa b, koniec ułamka" role="math"><math><mi>r</mi><mo>=</mo><mfrac><mrow><mi>a</mi><mi>h</mi></mrow><mrow><mi>a</mi><mo>+</mo><mn>2</mn><mi>b</mi></mrow></mfrac></math></span>, <span aria-label="r, równa się, początek ułamka, a h, mianownik, a, plus, b, plus, c, koniec ułamka" role="math"><math><mi>r</mi><mo>=</mo><mfrac><mrow><mi>a</mi><mi>h</mi></mrow><mrow><mi>a</mi><mo>+</mo><mi>b</mi><mo>+</mo><mi>c</mi></mrow></mfrac></math></span>
| równoboczny | |
| równoramienny | |
| prostokątny | |
| dowolny |
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
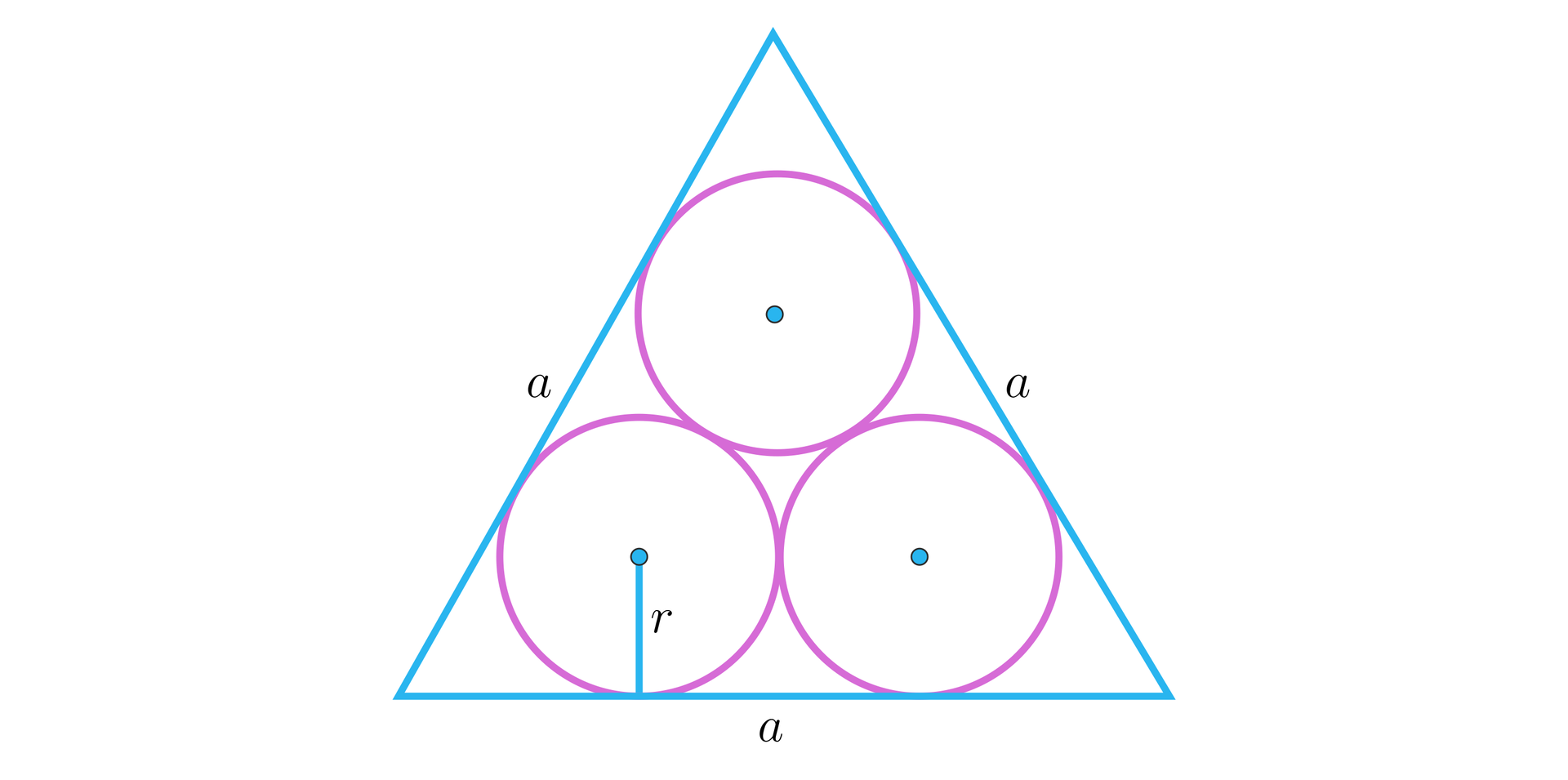
W trójkąt równoboczny o boku wpisano trzy przystające okręgi styczne zewnętrznie oraz styczne do boków trójkąta (rysunek). Wyznacz długość promienia tych okręgów.
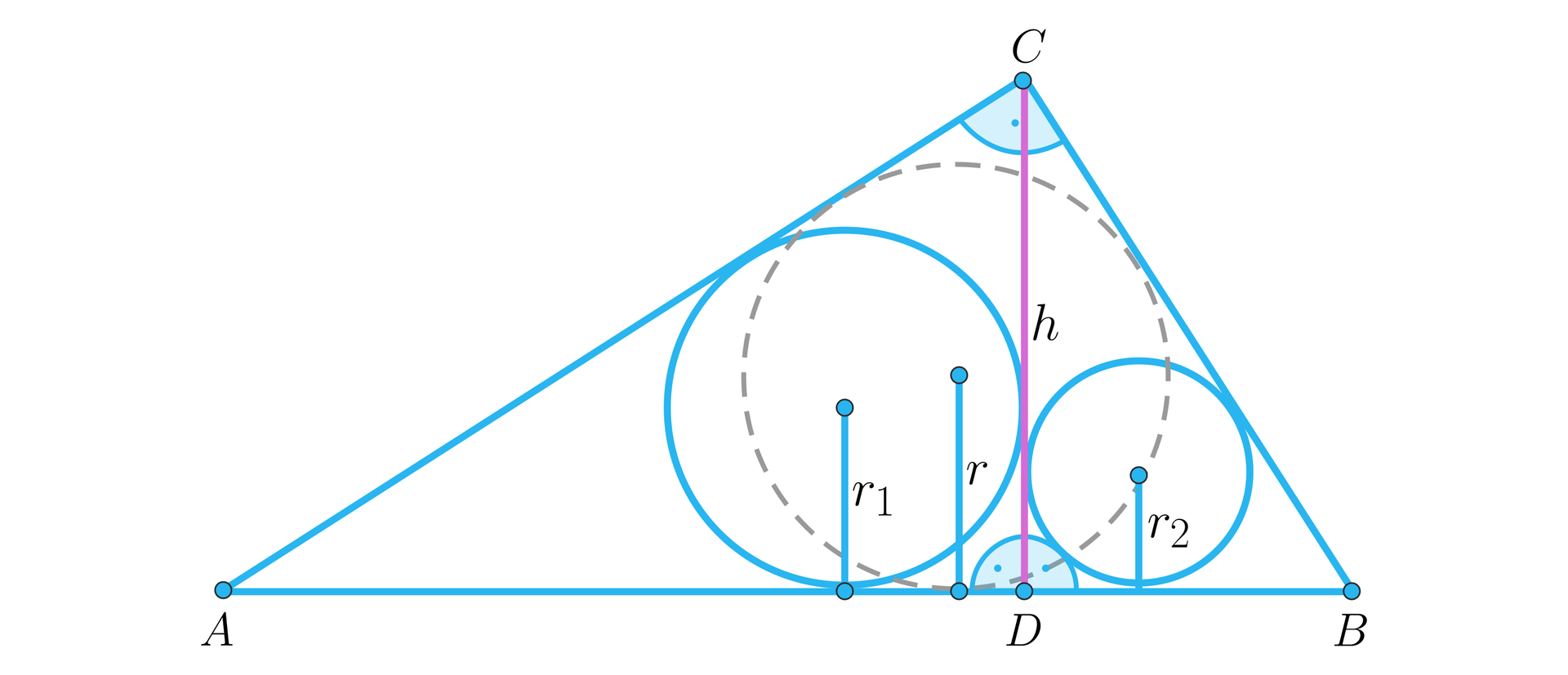
Dany jest trójkąt prostokątny , w którym kąt przy wierzchołku jest prosty. W trójkącie tym poprowadzono wysokość . Wykaż że , gdzie , , są odpowiednio długościami promieni okręgów wpisanych w trójkąty , i .
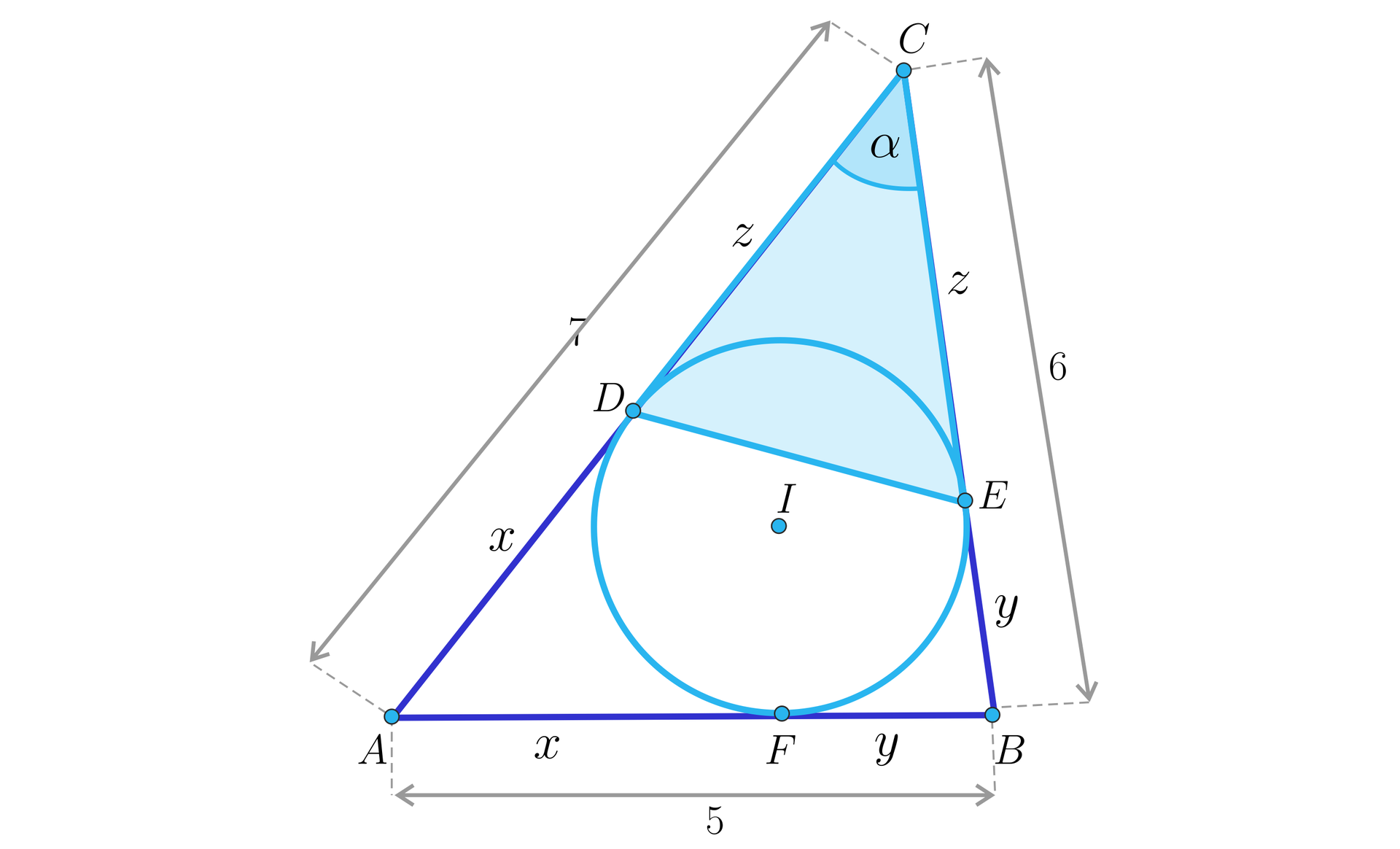
Prosta przechodząca przez środek okręgu wpisanego w trójkąt przecięła boki i w punktach odpowiednio i . Prosta ta podzieliła obwód tego trójkąta na połowy. Przyjmijmy, że pole trójkąta jest równe , natomiast pole czworokąta jest równe .
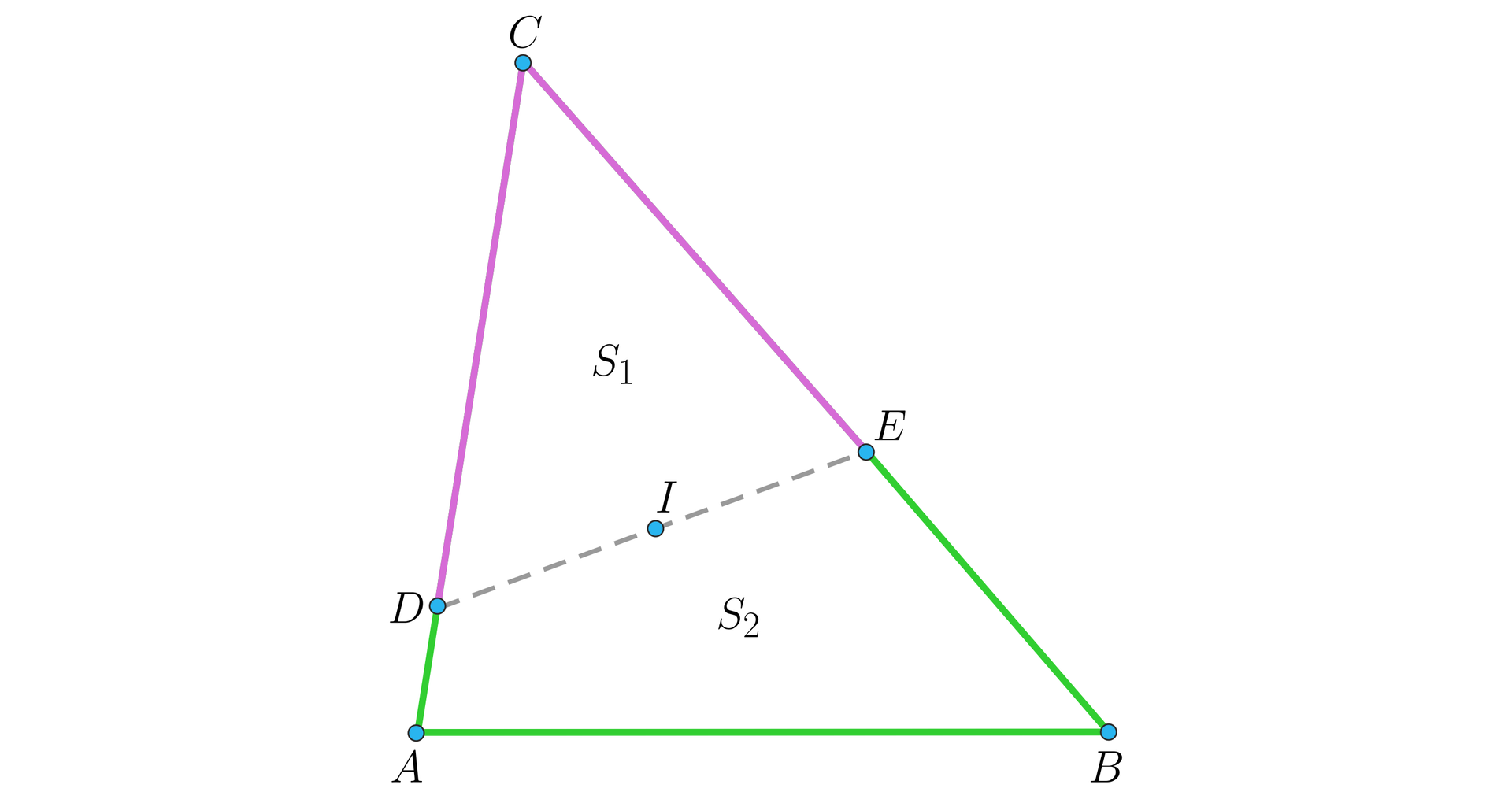
Wówczas:
- wartość zależy od kąta nachylenia prostej do podstawy
W trójkąt prostokątny o kącie prostym przy wierzchołku i wysokości wpisano okrąg o promieniu (rysunek). Okrąg ten jest styczny do przeciwprostokątnej w punkcie . Niech oznacza pole trójkąta .
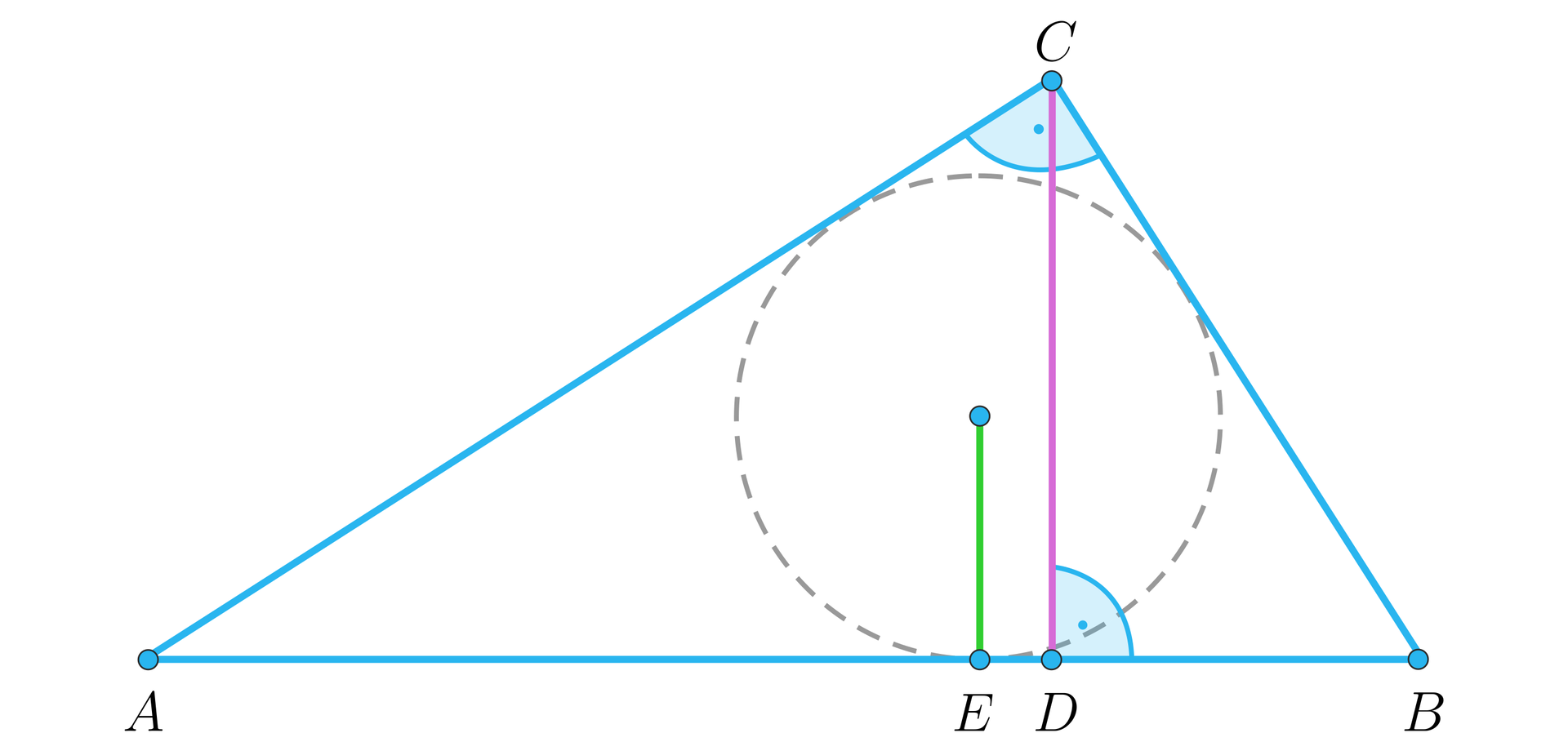
Wskaż zdania prawdziwe:
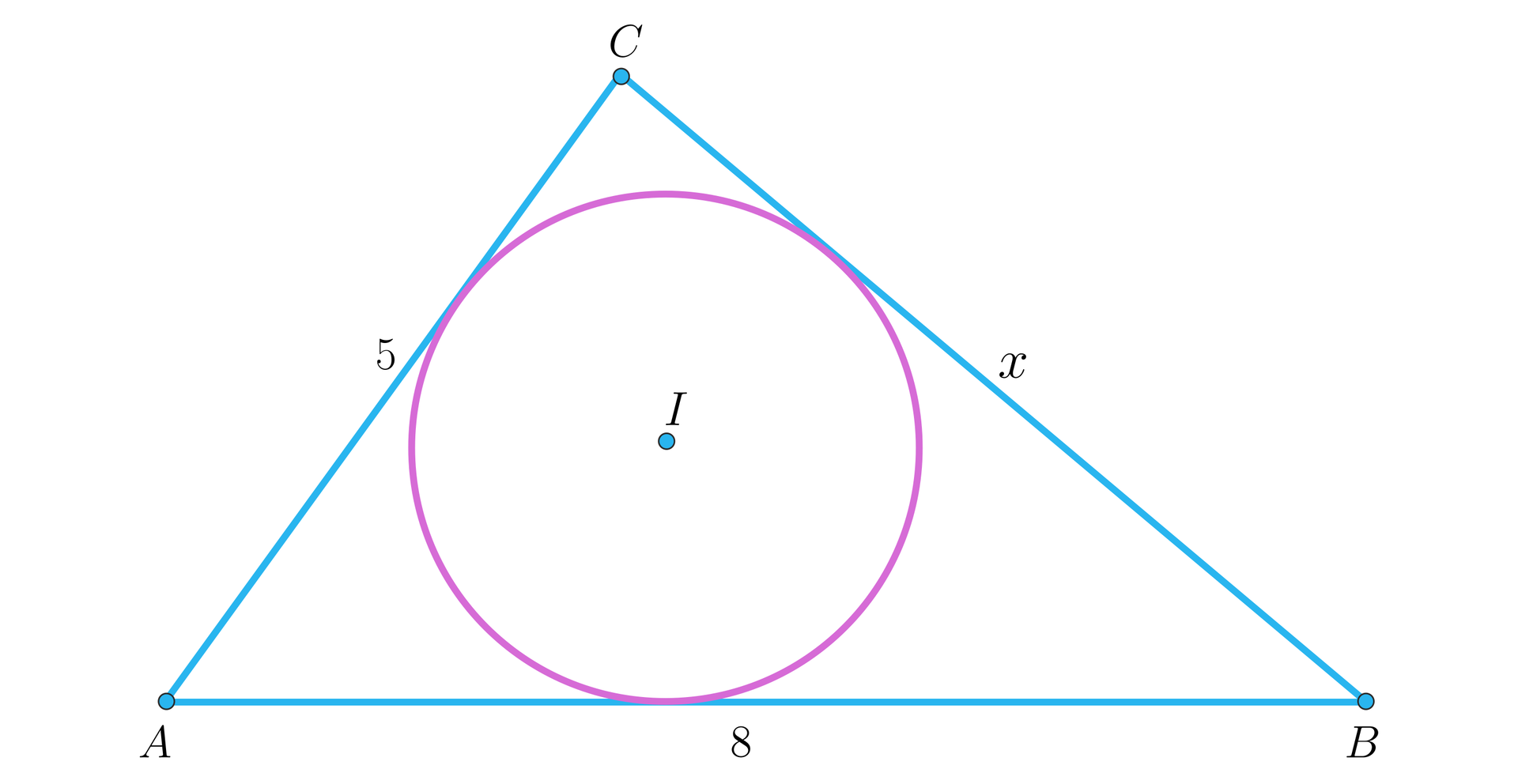
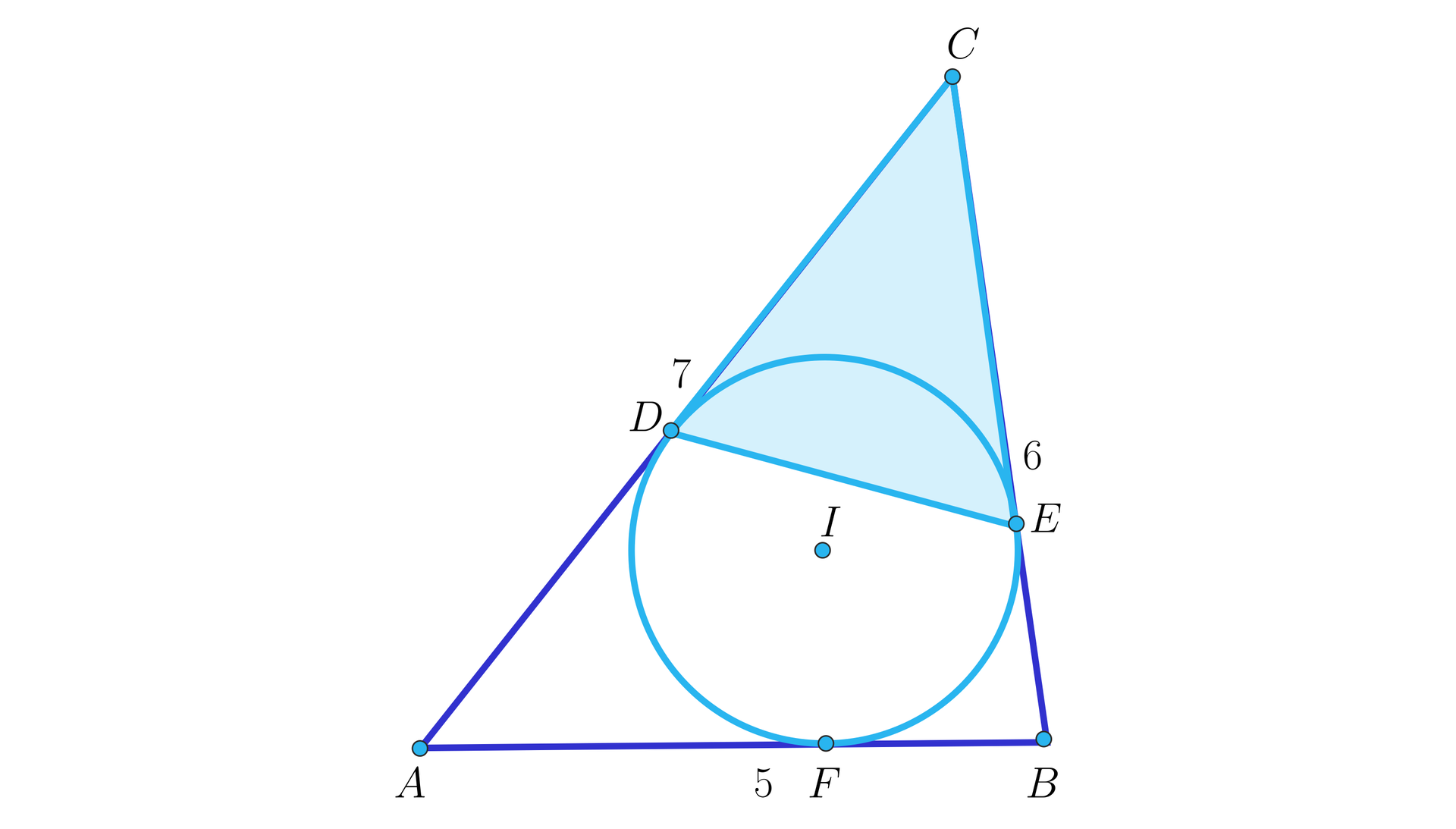
Okrąg wpisany w trójkąt o bokach długości , , , jest styczny do boków i w punktach i . Oblicz pole trójkąta .
Promień okręgu wpisanego w trójkąt o bokach i jest równy , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.