Średnia, mediana, dominanta
Próbując poznać fragment otaczającego nas świata możemy zastosować metody ilościowe albo jakościowe.
Przeprowadzając badania ilościowe, mamy do czynienia ze zbiorami danych. Jeżeli tych danych jest kilka, to możemy stwierdzić, która jest największa, która najmniejsza, która występuje najczęściej itp. Jednak, żeby wyciągnąć wniosek o jakimś zjawisku, potrzebujemy tych danych dużo więcej. Im więcej danych zbierzemy, tym trafniejsze będzie nasze wnioskowanie. Oczywiście najlepiej byłoby mieć wszystkie informacje, co zwykle jest niemożliwe lub bardzo kosztowne. Dlatego najczęściej bierzemy pod uwagę jedynie niektóre dane z tzw. próby. Na przykład producent spodni męskich przeznaczonych na rynek polski powinien dysponować informacją o zapotrzebowaniu na poszczególne rozmiary spodni. Dobrze przeprowadzone badania ilościowe pozwolą z dużą trafnością odpowiedzieć na to pytanie.
Zapytaliśmy uczniów pewnej szkoły, ile godzin przeznaczają tygodniowo na naukę. Każdą otrzymaną odpowiedź zanotowaliśmy, zapisując też informację o płci ucznia i o klasie. Otrzymane dane zestawiliśmy w tabeli.
Nr badanego ucznia | Płeć | Klasa | Liczba godzin tygodniowo przeznaczonych na naukę |
Nasza tabela składa się z wierszy. Bezpośrednia obserwacja takiej tabeli niewiele daje. Danych jest zbyt wiele, żeby je przyswoić i wyciągnąć z nich wnioski. Dane te wymagają pewnego zorganizowania w zależności od tego, co chcemy z nich wywnioskować. Gdy chcemy odpowiedzieć na pytanie, czy dziewczęta poświęcają tygodniowo na naukę więcej czasu niż chłopcy, to musimy pogrupować nasze dane ze względu na płeć. Gdy interesuje nas, której klasy uczniowie poświęcają najwięcej czasu na naukę, pogrupujemy je ze względu na klasę.
Oczywiście samo pogrupowanie danych jeszcze nie rozwiązuje problemu. Aby porównać interesującą nas wielkość, w każdej z wyodrębnionych grup, obliczamy pewną liczbę, reprezentującą tę wielkość. Tego typu liczby nazywamy parametrami danych statystycznych, czy też statystykami.
Zacznijmy od takich parametrów, które w pewien sposób wyznaczają „środek” danej próby, czyli są tzw. miarami tendencji centralnej. Należą do nich różnego rodzaju średnie, mediana i dominanta.
Średnią arytmetyczną liczb rzeczywistych nazywamy liczbę .
W celu ustalenia średniej ceny sprzedaży pewnej książki zbadano jej cenę w ośmiu księgarniach. Ceny te były równe: . Średnia cena tej książki jest więc równa:
Średniej często używa się, żeby stworzyć jakiś wzorzec. Jeżeli obliczę, na podstawie rachunków z ostatniego roku, że średnia miesięczna opłata w moim mieszkaniu za energię elektryczną wynosi , to mogę przewidywać, że w kolejnych miesiącach też zapłacę około miesięcznie, przy założeniu, że warunki nie zmienią się (nie kupię nowego sprzętu elektrycznego, nie zmieni się cena prądu itp). Średnia jest wielkością, z którą wygodnie jest porównywać konkretne dane. Jeżeli z badań przeprowadzonych na grupie . licealistów wynika, że średnio poświęcają na naukę minuty dziennie, to możesz oszacować, czy uczysz się więcej, czy mniej niż przeciętny licealista.
Średnia cena pięciu filmów zakupionych przez pana Kowalskiego jest równa 24 zł. Po dokupieniu szóstego filmu, średnia cena wzrosła do . Ile kosztował szósty z filmów?
Za pięć filmów zapłacono . Oznaczmy cenę szóstego filmu przez . Wtedy średnia cena zakupu filmu jest równa . Cenę tę mamy podaną, jest ona równa . Pozostaje rozwiązać równanie
Stąd , czyli .
Zauważ, że jeżeli średnia arytmetyczna pewnych liczb jest równa i dodasz do nich liczbę , to po dodaniu średnia nowego zestawu liczb zwiększy się. Jeżeli dodasz liczbę , to średnia nowego zestawu liczb zmniejszy się. Jeżeli dodamy , to średnia nie ulegnie zmianie.
W pewnej szkole są trzy klasy trzecie. Średni wynik próbnej matury uczniów klasy , liczącej osób, jest równy punktów, średni wynik klasy , liczącej uczniów, jest równy punktów, a średni wynik klasy , liczącej uczniów, to punktów. Ile jest równy średni wynik próbnej matury w całej szkole?
Zaczniemy od zsumowania liczby punktów uzyskanych z tej matury przez wszystkich uczniów w szkole. Klasa : punktów.
Klasa : punktów.
Klasa : punktów.
W sumie w całej szkole uczniowie zdobyli punktów. Ponieważ uczniów w klasach trzecich tej szkoły jest , więc szukana średnia jest równa .
Zauważ, że średnia ta nie jest średnią arytmetyczną podanych średnich w poszczególnych klasach, czyli nie jest ona równa:
Tak jest, gdyż liczby osób w klasach są różne. Średni wynik klasy III a w większym stopniu wpływa na obliczony średni wynik szkoły niż wynik każdej z pozostałych dwóch klas, ponieważ klasa jest najliczniejsza. Spośród wszystkich uczniów klas trzecich tej szkoły to uczniowie klasy , więc możemy przyjąć, że mamy uczniów, z których każdy ma wynik punktów. Analogicznie możemy przyjąć, że mamy uczniów z wynikiem średnim punktów i uczniów z wynikiem punktów. Średni wynik jest więc równy:
Liczebności, z jakimi występowały wyniki i , a więc liczby i , są wagami tych wyników, a obliczona średnia to średnia ważona.
Średnią ważoną liczb , którym przyporządkowane są odpowiednio dodatnie wagi , nazywamy liczbę .
Uwaga
Niekiedy wygodniej jest zapisać wzór w postaci:
Wtedy przyjmujemy, że wagami, z jakimi występują liczby , są ułamki:
Ułamki te są dodatnie i ich suma jest równa . Zatem
gdzie .
Jeżeli liczymy średnie z dwóch równolicznych grup danych, to średnia ze wszystkich liczb jest średnią arytmetyczną średniej policzonej w pierwszej grupie i średniej policzonej w drugiej grupie. Jeżeli jednak grupy nie są równoliczne, to średnia wszystkich liczb najczęściej nie jest średnią z policzonych wcześniej średnich w każdej grupie.
Aby zaliczyć przedmiot „Matematyka” na pewnym kierunku studiów, student musi uzyskać oceny: z ćwiczeń, laboratorium i egzaminu, przy czym każda z ocen musi być pozytywna (co najmniej równa ). Wówczas ocena z przedmiotu „Matematyka” jest średnią ważoną tych trzech ocen: ocena z ćwiczeń ma wagę , z laboratorium wagę , a ocena z egzaminu wagę . W tabeli zestawiono oceny cząstkowe Tomka i Michała. Jaką ocenę otrzyma każdy z nich na zaliczenie?
ćwiczenia | laboratorium | egzamin | |
Tomek | |||
Michał |
Średnia ważona ocen Tomka jest równa .
Średnia ważona ocen Michała jest równa .
Zwróć uwagę, że mimo iż obaj chłopcy cząstkowe oceny mieli takie same, czyli oraz na koniec dostaną inną ocenę. Tak jest dlatego, gdyż Tomek ma najwyższą ocenę z laboratorium, czyli tę o najniższej wadze, za to Michał najwyższą ocenę ma z egzaminu, czyli tę o najwyższej wadze.
Średnia arytmetyczna ma pewne wady. Bardzo duży wpływ na nią mają wartości skrajne, czyli te największe i najmniejsze, zwłaszcza jeżeli są wyraźnie większe albo mniejsze od pozostałych. W takich przypadkach średnia nie oddaje prawdziwego poziomu interesującej nas wielkości.
Chcemy rozpocząć pracę w pewnej firmie. Dowiadujemy się, że średnia pensja w tej firmie to . Czy należy się spodziewać, że będziemy zarabiać około ? Otóż niekoniecznie. Gdyby w tej firmie pracowało osób, z których 8 to szeregowi pracownicy o zarobkach odpowiednio: i oraz prezes, którego zarobki to , to średnia pensja w tej firmie jest równa . Należy przypuszczać, że nowo zatrudniony pracownik w takiej firmie nie będzie zarabiał więcej niż najwięcej zarabiający aktualnie pracownik szeregowy, a więc .
W takich przypadkach, gdy wyniki skrajne znacznie odbiegają od pozostałych i w efekcie zaburzają średnią, lepiej posłużyć się inną miarą tendencji centralnej. Możemy np. obliczyć medianę.
Medianą (wartością środkową) uporządkowanego w kolejności niemalejącej zbioru liczb jest:
dla nieparzystej liczby środkowy wyraz ciągu, czyli wyraz
dla parzystej liczby średnia arytmetyczna dwóch środkowych wyrazów ciągu, czyli .
Policzmy medianę zarobków w firmie z przykładu . Pensje już są ustawione w ciąg niemalejący
Medianę liczymy z liczb, czyli środkową jest stojąca na pozycji piątej. Mediana jest więc równa . Wielkość ta dużo lepiej, niż średnia arytmetyczna oddaje realia zarobków szeregowych pracowników w rozważanej firmie.
Średnia arytmetyczna zestawu danych: jest równa . Oblicz medianę tego zestawu danych.
Suma danych liczb jest równa: . Ponieważ średnia arytmetyczna tych danych jest równa , otrzymujemy równanie , stąd . Mamy więc . Ustawiamy dane liczby w niemalejący ciąg
Liczba wyrazów ciągu jest równa , a więc jest parzysta. Stąd mediana jest równa średniej arytmetycznej wyrazów stojących na dwóch środkowych pozycjach. W tym przypadku na czwartej i piątej. Jest więc równa .
Innym sposobem na zmniejszenie wrażliwości średniej na wyniki skrajne jest odrzucenie pewnej liczby największych i najmniejszych danych i policzenie średniej z pozostałych danych. Taka średnia nosi nazwę średniej ucinanej (obciętej). Spotykamy ją w liczeniu noty końcowej przyznawanej przez sędziów w wielu dyscyplinach sportowych, np. w skokach narciarskich, jeździe figurowej na lodzie, czy gimnastyce artystycznej.
Sposobem na znalezienie „środka” danej próby jest podanie tzw. dominanty. Przydaje się ona szczególnie w tych przypadkach, gdy opisywane wielkości nie mają wartości liczbowej, czyli nie można policzyć dla nich średniej czy mediany.
Dominantą (modą, wartością najczęstszą) nazywamy tę wartość, która występuje w próbie najczęściej.
W sondzie ulicznej stu losowo wybranym osobom zadano pytanie: jaką herbatę piją najchętniej? Wyniki badania przedstawiono na diagramie.
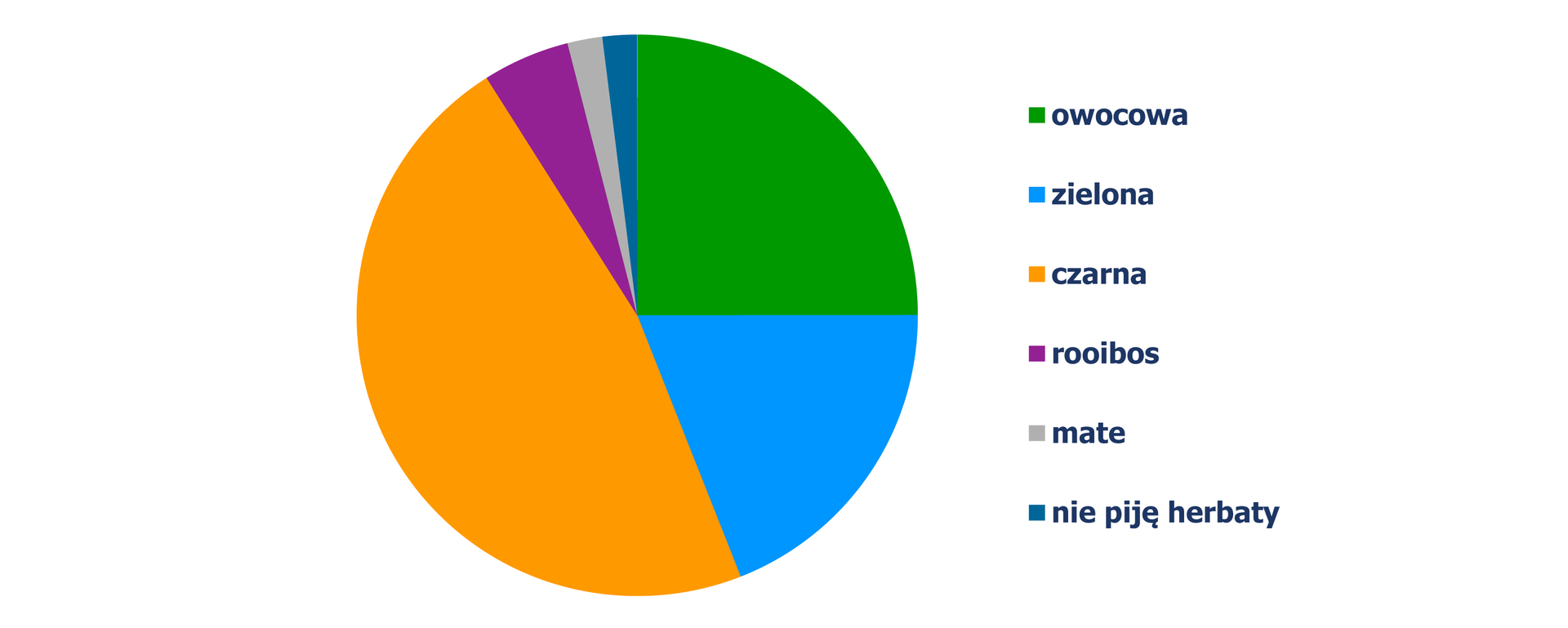
Dominantą tego badania jest herbata czarna.
W pewnym domu kultury prowadzone są zajęcia plastyczne, w których bierze udział dzieci. Porównaj ze sobą średnią wieku, medianę i dominantę uczestników tych zajęć.

Średnia wieku uczestników jest równa:
Dominantą jest wiek lat. Medianą będzie średnia arytmetyczna wieku stojącego na i pozycji w niemalejącym ciągu wieku uczestników. Zauważmy, że jeżeli zsumujemy liczby siedmio-, ośmio- i dziewięciolatków, otrzymamy osób, czyli od pozycji do pozycji będzie stała wartość lat, więc mediana jest równa .
Średnie, mediana, dominanta, czyli statystyki wyznaczające środek zestawu danych. Zadania
Średnia arytmetyczna liczb: jest równa . Wtedy mediana jest równa
Mediana zestawu danych: jest równa . Wówczas
Rzucono kością sześć razy i otrzymano wyniki: . Wtedy
- mediana i średnia arytmetyczna są sobie równe
- mediana jest większa niż średnia arytmetyczna
- średnia arytmetyczna jest większa niż mediana
- nie istnieje mediana tego zestawu danych
W pewnej grupie rodzin zbadano liczbę dzieci i dane przedstawiono na wykresie.

Mediana przedstawionych na wykresie danych jest równa
Mediana liczb: wynosi . Wtedy liczba spełnia warunek
Średnia ważona liczb: z wagami odpowiednio: , , jest równa . Wtedy liczba jest równa
Do zestawu liczb dopisujemy kolejną.
Przeciągnij liczby z dolnej sekcji do górnej.
<math><mn>9</mn></math>, <math><mn>6</mn></math>, <math><mn>6,5</mn></math>, <math><mn>10</mn></math>, <math><mn>1</mn></math>, <math><mn>5,75</mn></math>, <math><mn>7</mn></math>, <math><mn>4,5</mn></math>
| liczby, które zwiekszą średnią arytmetyczną zestawu | |
|---|---|
| liczby, które zmniejszą średnią arytmetyczną zestawu | |
| liczby, które nie zmienią średniej arytmetycznej zestawu |
Połącz w pary zestawy danych z ich średnimi arytmetycznymi.
5,5,5,7,8, 4,6,8,10,12, 5,6,12,13,14, 2,3,5,5,5, 5,5,5,5,5
| 5 | |
| 8 | |
| 10 | |
| 4 | |
| 6 |
Połącz w pary zestawy danych z ich medianą.
8,5,1,9, 5,5,5,5, 5,6, 10,6, 1,4,10,12, 1,20, 10,1
| 5 | |
| 6 | |
| 6,5 | |
| 7 | |
| 5,5 |
Wyniki sprawdzianu z matematyki i z języka polskiego w klasie są przedstawione na diagramie
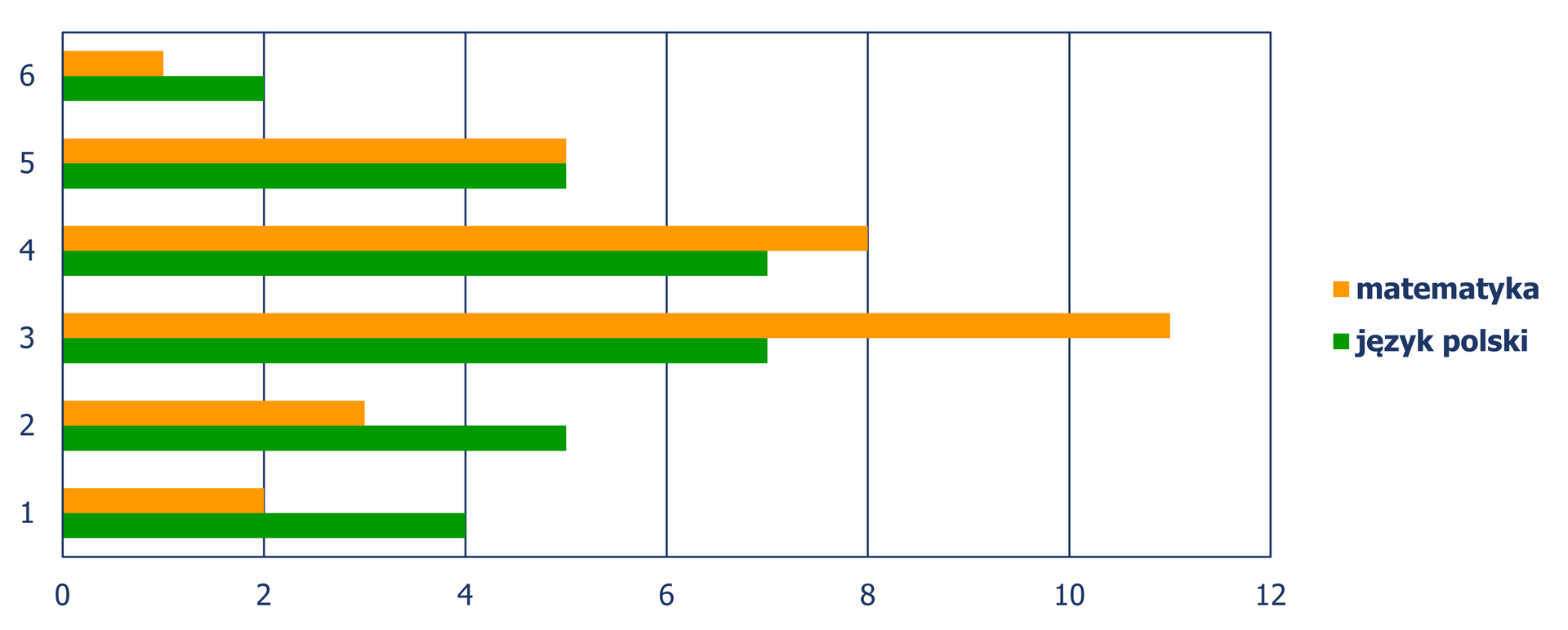
Ilu uczniów ze sprawdzianu z matematyki otrzymało ocenę wyższą niż średnia ocen?
Ilu uczniów ze sprawdzianu z języka polskiego otrzymało ocenę niższą niż mediana ocen?
W tabeli zestawiono oceny z matematyki na koniec roku uczniów pewnej klasy.
Ocena | ||||||
Liczba ocen |
Oblicz liczbę piątek, jeżeli średnia ocen z matematyki w tej klasie jest równa .
W sklepie przygotowano mieszankę trzech rodzajów cukierków składającą się z cukierków w cenie za , cukierków w cenie za kg oraz cukierków w cenie za . Ile powinien kosztować mieszanki?
Średni staż pracy robotników w pewnym zakładzie jest równy lat. Jeżeli dodać do badanych brygadzistę, to średni wiek pracy zwiększy się do lat. Ile lat pracuje w tym zakładzie brygadzista?
Średnia wieku uczestników wycieczki wynosiła lat. Jeżeli doliczymy do tej średniej wiek opiekuna, który ma lat, to średnia zwiększy się do lat. Ilu było uczestników wycieczki?
W pewnej firmie średnia pensja jest równa . O ile procent zwiększy się średnia pensja, jeżeli każdy z pracowników dostanie podwyżkę?
o
o
W celu zakupienia obuwia dla zawodników drużyny piłkarskiej sprawdzono rozmiary obuwia poszczególnych zawodników i dane umieszczono na diagramie.

Oblicz medianę, modę i średnią arytmetyczną rozmiaru.
W pewnej szkole dwie klasy trzecie napisały próbną maturę z matematyki. W klasie , liczącej uczniów, średni wynik z tej matury wyniósł , a w klasie , liczącej uczniów średni wynik z tej matury wyniósł . Jaki jest średni wynik z próbnej matury w tej szkole?
Poniżej przedstawiono uporządkowane niemalejąco zestawy danych, których mediana jest równa 5. Połącz je w pary z ich średnimi.
3, x, 6, 7, 3, x, 10, 1, x, 6, 1, 3, x, 7
| 6 | |
| 4 | |
| 5 | |
| 4,5 |
Średnia arytmetyczna trzech liczb: jest równa . Oblicz, ile wynosi średnia arytmetyczna podanych liczb:
Trzech uczniów napisało maturę z matematyki, zdobywając średnio punktów na możliwych. Mediana ich wyników jest równa punktów. Ile punktów zdobyli poszczególni uczniowie na maturze z matematyki?
Małgosia na koniec roku szkolnego, uzyskała średnią ocen . Spośród dziesięciu przedmiotów otrzymała tylko jedną , a poza tym same i . Oblicz, ile na świadectwie miała Małgosia.