Symetralna odcinka

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DWBctl6fV
Prosta jest symetralną odcinka . Punkt jest środkiem tego odcinka. Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DWBctl6fV
- Prosta jest prostopadła do odcinka .
- Prosta przechodzi przez środek odcinka .
- Punkty i leżą w tej samej odległości od punktu .
Symetralna odcinka to prosta prostopadła do tego odcinka, przechodząca przez jego środek.

.
Każdy z punktów leżących na symetralnej odcinka jest równo oddalony od obu końców tego odcinka.
Konstrukcja symetralnej odcinka.
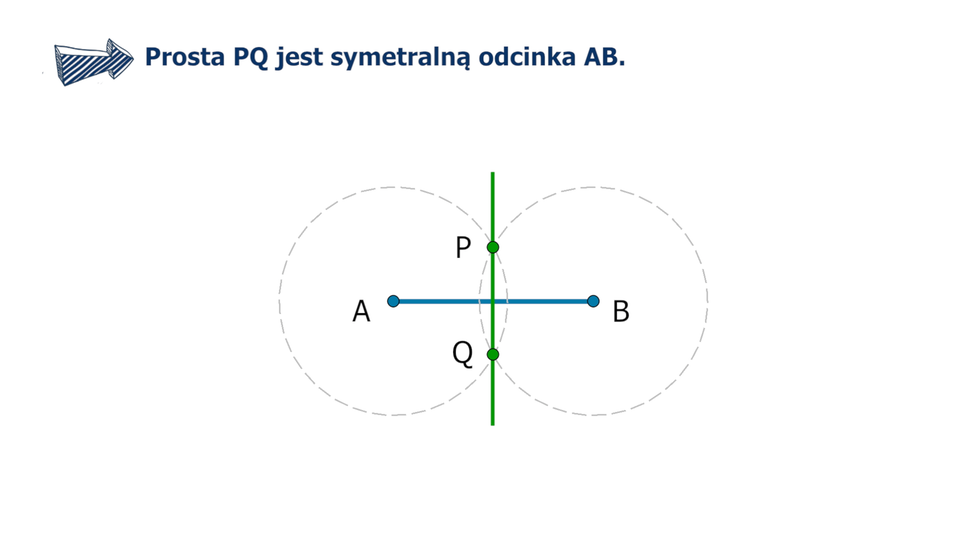
Film dostępny na portalu epodreczniki.pl
Animacja
Narysuj odcinek i jego symetralną.
Symetralna odcinka
- jest prostopadła do tego odcinka
- jest równoległa do tego odcinka
- przechodzi przez jeden z końców odcinka
- jest nachylona do odcinka pod kątem
Symetralna odcinka to
- dowolna prosta prostopadła do odcinka
- prosta prostopadła do odcinka i przechodząca przez jego środek
- zbiór punktów równo oddalonych od końców odcinka
- prosta, na której leży odcinek
Proste i przecinają się pod kątem . Na prostej obrano dwa rożne punkty i tak, jak na rysunku. Jaką miarę ma kąt utworzony przez prostą i symetralną odcinka ?

Zaznacz punkt tak, by symetralna odcinka przechodziła przez punkt . Ile takich punktów możesz zaznaczyć ? Narysuj figurę złożoną z wszystkich takich punktów .
Wskaż rysunek, na którym prosta jest symetralną odcinka .

- I
- II
- III
- IV