Symulacja interaktywna
Polecenie 1
Zapoznaj się z przykładami wykresów funkcji różnowartościowych i funkcji, które nie są różnowartościowe. Zmieniaj wzór funkcji oraz równanie prostej równoległej do osi .
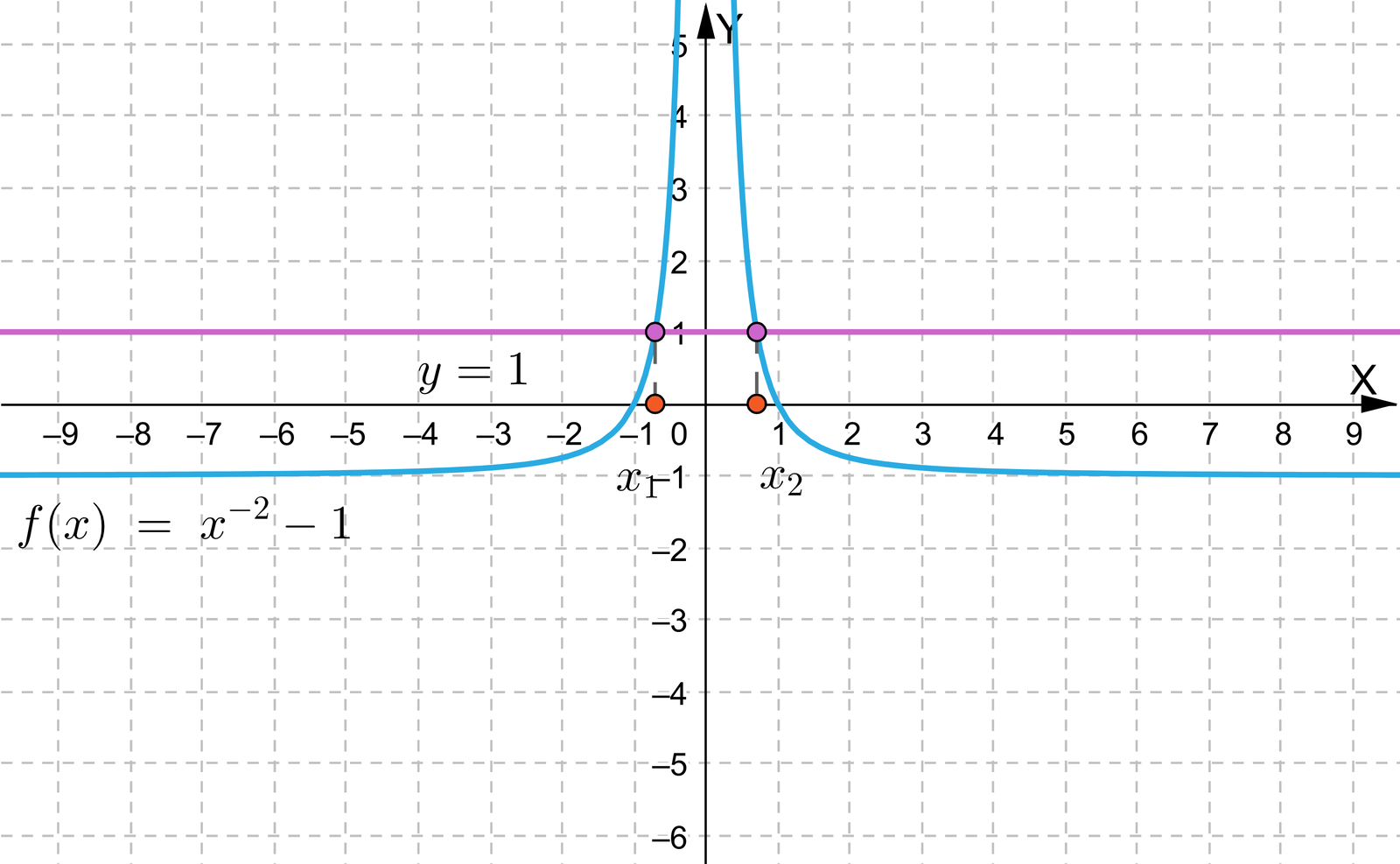
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D15Ae8R18
Polecenie 2
Dana jest funkcja . Zbadaj, czy funkcja jest różnowartościowa.
Polecenie 3
Dana jest funkcja . Zbadaj, czy funkcja jest różnowartościowa.