Układ równań z dwiema niewiadomymi – opisywanie związków między wielkościami za pomocą równań

Film dostępny na portalu epodreczniki.pl
Animacja
Równaniem z dwiema niewiadomymi nazywamy równanie, w którym występują dwie niewiadome.
Na przykład:
Równaniem pierwszego stopnia z dwiema niewiadomymi nazywamy równanie, w którym obie niewiadome występują w pierwszej potędze.
Na przykład:
Równanie pierwszego stopnia z dwiema niewiadomymi ma nieskończenie wiele rozwiązań.
RbFxNE5ZSPA7P1 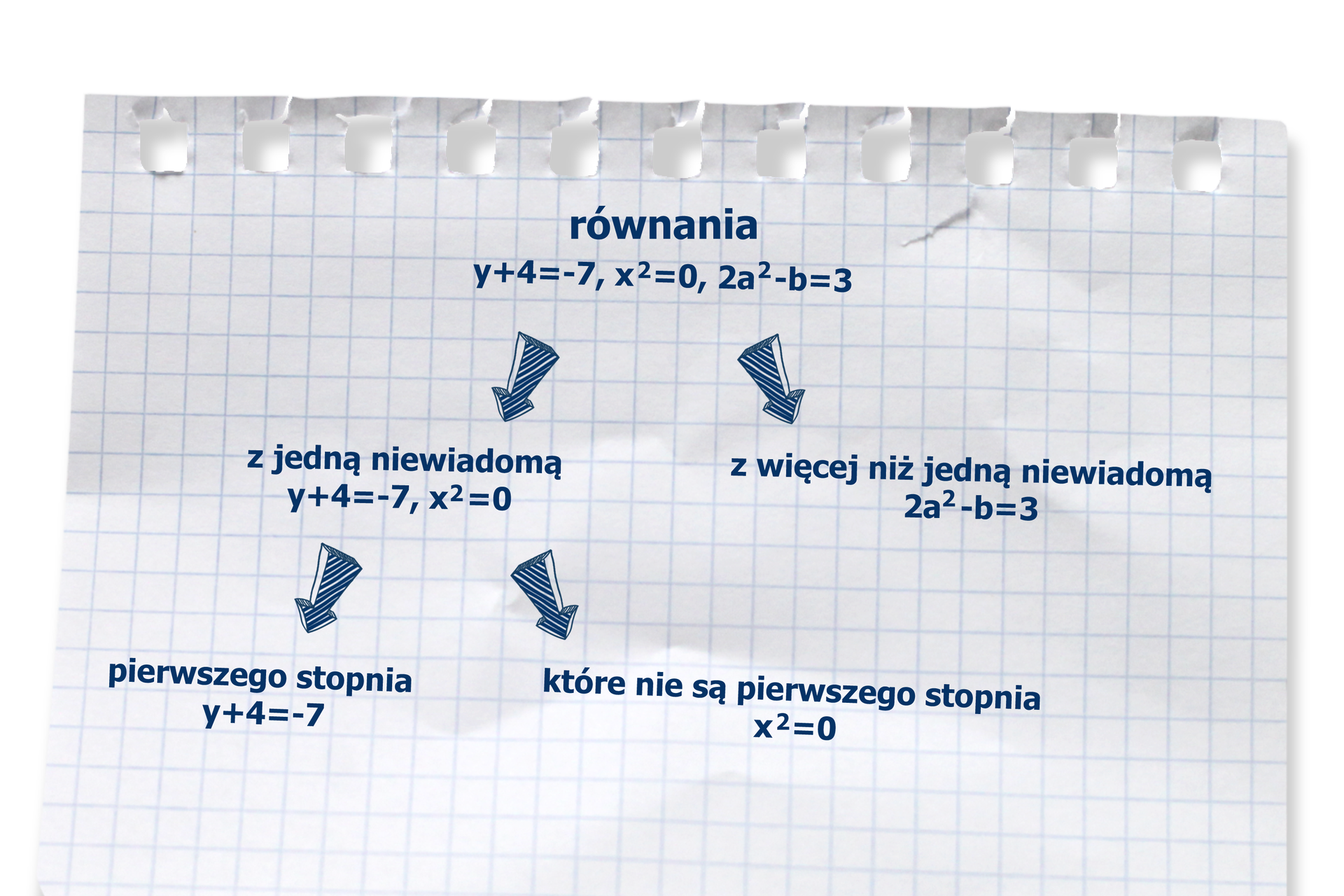 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Układem równań pierwszego stopnia z dwiema niewiadomymi nazywamy dwa równania pierwszego stopnia z co najwyżej dwiema niewiadomymi, połączone spójnikiem „i”, który symbolizuje klamra.
Na przykład
Układy równań wykorzystujemy do zapisywania i rozwiązywania takich zadań, w których należy zastosować więcej niż jedną niewiadomą.
Spośród poniższych układów równań wybierz układy równań pierwszego stopnia z dwiema niewiadomymi.
Zapisz układ równań, który opisuje podaną sytuację. Skorzystaj z rysunku.

Asia, kupując truskawek i malin, zapłaciła a Maciek, kupując truskawek i malin, zapłacił .
Marysia, kupując kg borówek i czereśni, zapłaciła , a Jacek, kupując czereśni i borówek, zapłacił .
Ala, kupując truskawek i borówek, zapłaciła , a Krzyś, kupując truskawek i borówek, zapłacił .
Zapisz układ równań, który opisuje podaną sytuację. Skorzystaj z rysunku.
Beata, kupując szampon i kremy do twarzy, zapłaciła , a Alicja, kupując krem i szampony, zapłaciła Oznacz
- cena jednego szamponu do włosów
- cena jednego kremu do twarzyR1DvjVTNaQ2IM1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.- masa większego klocka - masa mniejszego klocka
Agnieszka, kupując opakowania ptasiego mleczka i mleczne czekolady, zapłaciła . Natomiast Bartek, kupując mleczne czekolady i opakowania ptasiego mleczka, zapłacił .
- cena jednego opakowania ptasiego mleczka
- cena jednej mlecznej czekoladyRzvXDj5nuelqE1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.- masa jednej brzoskwini - masa jednej gruszki
Które zdanie opisuje układ równań ?
- Liczba o mniejsza od jest razy większa od .
- Liczba o mniejsza od różnicy liczb i jest równa średniej arytmetycznej liczby i dwukrotności liczby .
- Liczba o mniejsza od jest razy większa od . Liczba o mniejsza od różnicy liczb i jest równa średniej arytmetycznej liczby i dwukrotności liczby .
- Liczba o mniejsza od jest razy większa od . Liczba o większa od różnicy liczb i jest równa średniej arytmetycznej liczby i dwukrotności liczby .
- Liczba o większa od jest razy mniejsza od . Liczba o mniejsza od różnicy liczb i jest równa średniej arytmetycznej liczby i dwukrotności liczby .

Film dostępny na portalu epodreczniki.pl
Animacja
Zapisz układy równań opisujące sytuację przedstawioną na rysunkach.
Ra28ijNPmFV4D1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.RovhS9sYQb69L1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R8EVVhkZO5ToU1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Uzupełnij wyrażenia, aby otrzymany układ równań opisywał poniższą sytuację.
Za stół i krzesła zapłacono . Cena krzesła jest trzykrotnie mniejsza od ceny stołu.
- cena stołu (w )
- cena krzesła (w )Za zeszyt i ołówków zapłacono . Dwa zeszyty kosztują tyle, co pięć ołówków.
- cena jednego zeszytu (w )
- cena jednego ołówka (w )Mama i tata mają razem lat. Tata jest o lat starszy od mamy.
- wiek mamy
- wiek tatyAnia jest o lat młodsza od swojego brata. Za dwa lata będzie od niego razy młodsza.
- wiek Ani
- wiek brata AniZosia i Ala mają razem lat. Za lat będą miały razem lata.
- wiek Zosi
- wiek Ali
Uzupełnij wyrażenia, aby otrzymany układ równań opisywał poniższą sytuację.
Masa opakowań ciastek i paczek cukierków jest równa . Masa jednego opakowania ciastek jest razy większa niż masa jednej paczki cukierków.
- masa jednego opakowania ciastek
- masa jednego opakowania cukierkówLiczba jest razy mniejsza od liczby . Średnia arytmetyczna liczb i jest dwa razy większa od liczby .
- wartość pierwszej liczby
- wartość drugiej liczbyNa wycieczkę pojechało dziewcząt i chłopców, razem osób. Liczba chłopców jest o połowę większa od liczby dziewcząt.
- liczba dziewcząt
- liczba chłopcówW skarbonce jest monet dwuzłotowych i monet pięciozłotowych, razem . Liczba monet pięciozłotowych jest o mniejsza od liczby monet dwuzłotowych.
- liczba monet dwuzłotowych
- liczba monet pięciozłotowych
Połącz w pary podane zdania z układami równań, które je opisują.
Liczba jest o większa od trzeciej części liczby . Średnia arytmetyczna liczb i jest o mniejsza od liczby . | |||
Liczba jest o mniejsza od trzeciej części liczby . Podwojona średnia arytmetyczna liczb i jest o większa od liczby . | |||
Liczba jest o większa od potrojonej liczby . Średnia arytmetyczna liczb i jest o mniejsza od różnicy liczb i . | |||
Liczba jest o mniejsza od potrojonej liczby . Średnia arytmetyczna liczby i podwojonej liczby jest o mniejsza od liczby . |
Jedno opakowanie kawy rozpuszczalnej jest droższe o od trzech opakowań herbaty. Za dwa opakowania kawy i opakowań herbaty należy zapłacić . Który układ równań należy rozwiązać, aby wyznaczyć cenę tych produktów?
Suma liczby i liczby jest równa , a sumy liczb i jest równe . Który układ równań należy rozwiązać, aby wyznaczyć wartości tych liczb?
W skarbonce jest w monetach pięciogroszowych, dwudziestogroszowe oraz monety dwuzłotowe. Średnia arytmetyczna liczby wszystkich monet w skarbonce jest równa .
Wskaż układy równań opisujące sytuację przedstawioną w zadaniu.
Cztery lata temu Adam był razy starszy od Agnieszki, a za lata będzie od niej razy starszy. Który układ równań należy rozwiązać, aby wyznaczyć wiek Adama i Agnieszki?
Zapisz układ równań, który opisuje następującą sytuację.
Różnica dwóch liczb wynosi . Znajdź te liczby, wiedząc, że jeżeli większą z nich zwiększymy o , a mniejszą zwiększymy trzykrotnie, to otrzymamy liczby równe.
Liczba jest o mniejsza od liczby . Połowa sumy liczb i jest o większa od liczby .
Liczba o większa od liczby jest o większa od liczby . Liczba o mniejsza od liczby jest równa liczbie .
Czwarta część liczby stanowi liczby . Liczba o większa od liczby jest o mniejsza od liczby .
Ustal niewiadome i zapisz układ równań, który opisuje następującą sytuację.
Marysia, kupując w księgarni ołówek i długopis, zapłaciła . Justyna, kupując takie same ołówki i taki sam długopis, zapłaciła .
W nadmorskim pensjonacie znajdują się pokoje czteroosobowe i trzyosobowe oraz pokoi dwuosobowych, razem pokoi. Pensjonat może przyjąć wczasowiczów.
Marek i Ala dostają co miesiąc kieszonkowe od swoich rodziców. W ciągu roku rodzeństwo otrzymało złotych. Miesięczne kieszonkowe Marka jest o niższe od kieszonkowego Ali.
W pewnym gospodarstwie hodowano gęsi, których pilnowały mniejsze psy. Zwierzęta miały razem nóg i głów.
Skrzynia z narzędziami waży . Masa narzędzi jest siedmiokrotnie większa niż masa pustej skrzyni.
Zapisz układy równań opisujące sytuację przedstawioną na rysunku.
