Wprowadzenie do trygonometrii
Przypomnijmy, że trójkąty są podobne, jeśli wszystkie ich odpowiednie kąty są równe (cecha kąt‑kąt‑kąt).
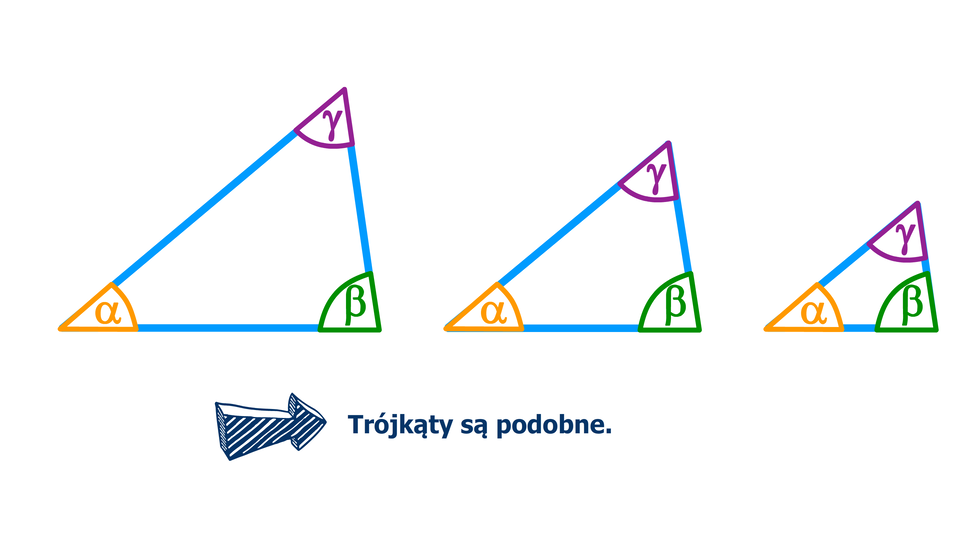
Film dostępny na portalu epodreczniki.pl
Animacja pokazuje trzy różnych wymiarów zdjęcia tej samej budowli w kształcie trójkątna ostrokątnego. Na zdjęciu największym zaznaczono kąty alfa, beta i gamma. Porównując, w dwóch etapach (zdjęcie największe i średnie a potem największe i najmniejsze) odpowiednie kąty tych budowli, zauważamy że odpowiednie kąty w tych trójkątach są tej samej miary, a więc trójkąty są podobne.
Korzystając z cechy podobieństwa kąt‑kąt‑kąt, możemy sprawdzić, czy dwa trójkąty prostokątne są podobne, gdy w każdym z nich znamy miarę jednego z kątów ostrych.

Film dostępny na portalu epodreczniki.pl
Animacja pokazuje trzy różnych wymiarów zdjęcia żaglówki, na których narysowano trójkąty prostokątne o kątach 90 stopni i alfa. W pierwszym trójkącie brakujący kąt beta równy 90 stopni minus alfa. W drugim trójkącie kąt beta prim równy 90 stopni minus alfa równy beta. W trzecim trójkącie kąt beta bis równy 90 stopni minus alfa równy beta, więc trójkąty są podobne.
W trójkącie prostokątnym kąt przy wierzchołku jest prosty, a miara kąta jest równa . W trójkącie prostokątnym kąt przy wierzchołku jest prosty, a miara kąta jest równa .
A zatem
Trójkąty i są więc podobne, co stwierdzamy, powołując się na cechę podobieństwa kąt‑kąt‑kąt.


W trójkątach podobnych pary odpowiednich boków są proporcjonalne – boki trójkątów i spełniają więc zależność
Wynika z tego, że każdy stosunek długości dwóch boków w trójkącie jest równy stosunkowi długości odpowiednich boków w trójkącie , np.
Rozpatrzmy trójkąt prostokątny , którego przyprostokątne i są równe .
Ponieważ trójkąt ten jest równoramienny, to miary jego kątów ostrych i są równe .
Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej tego trójkąta.
Ponieważ , stąd

Wówczas , , czyli , a także .
Każdy równoramienny trójkąt prostokątny jest podobny do trójkąta , co stwierdzamy na mocy cechy podobieństwa kąt‑kąt‑kąt. Zatem w każdym trójkącie prostokątnym, którego jeden z kątów ostrych jest równy , stosunek dowolnie wybranej przyprostokątnej do przeciwprostokątnej jest równy .
Pokażemy, że trójkąt prostokątny, w którym stosunek jednej z przyprostokątnych do przeciwprostokątnej jest równy , jest trójkątem, w którym oba kąty ostre są równe .
Oznaczając długość przeciwprostokątnej tego trójkąta przez , gdzie , zauważmy, że jedna z jego przyprostokątnych ma długość , a zatem (na podstawie twierdzenia Pitagorasa) druga przyprostokątna ma długość . Wobec tego dany trójkąt prostokątny jest równoramienny, więc każdy z jego kątów ostrych ma miarę
Rozpatrzmy trójkąt prostokątny , którego przyprostokątna jest równa , a przeciwprostokątna jest równa . Z twierdzenia Pitagorasa obliczamy .

Na prostej wybierzmy teraz punkt symetryczny do punktu względem punktu . Wtedy
bo odcinki i są symetryczne względem prostej . Wobec tego trójkąt jest równoboczny, a to jego wysokość poprowadzona do boku .

Wynika z tego, że w trójkącie kąt ostry leżący naprzeciwko przyprostokątnej ma miarę a kąt ostry leżący naprzeciwko przyprostokątnej ma miarę .
Rozpatrzmy trójkąt prostokątny , którego przyprostokątna jest równa , a przeciwprostokątna jest równa .
Z twierdzenia Pitagorasa obliczamy .

Wybierzmy na półprostej takie punkty i , że i .

Wtedy:
w trójkącie jest więc kąt ma miarę .
w trójkącie jest a zatem kąt ma miarę .
Zatem kąt ostry w trójkącie ma miarę większą niż i mniejszą niż .
Za pomocą kątomierza, można zmierzyć na rysunku, że kąt ten ma miarę około
Każdy trójkąt prostokątny, którego kąty ostre mają miary , jest podobny do trójkąta , opisanego w poprzednim przykładzie. Wobec tego w każdym takim trójkącie prostokątnym:
stosunek długości przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej jest równy ,
stosunek długości przyprostokątnej leżącej przy kącie do przeciwprostokątnej jest równy ,
stosunek długości przyprostokątnej leżącej naprzeciw kąta do drugiej przyprostokątnej jest równy , czyli .
Wynika z tego również, że:
w każdym trójkącie prostokątnym, w którym jedna z przyprostokątnych jest dwa razy krótsza od przeciwprostokątnej, kąt ostry leżący naprzeciw tej przyprostokątnej jest równy
w każdym trójkącie prostokątnym, w którym stosunek długości jednej z przyprostokątnych do długości przeciwprostokątnej jest równy , kąt ostry leżący naprzeciw tej przyprostokątnej jest równy ,
w każdym trójkącie prostokątnym, w którym stosunek długości jednej z przyprostokątnych do długości drugiej przyprostokątnej jest równy , kąt ostry leżący naprzeciw krótszej przyprostokątnej jest równy .