Przecinając równoległobok $ABCD$ prostą $k$ równoległą do boków $AD$ i $BC$ tego równoległoboku odcinamy z boków $AB$ i $CD$ odcinki $AE$ i $DF$ równej długości.

R1bTFT9GUzGxL

Ilustracja przedstawia równoległobok A B C D oraz prostą k równoległą do boków D A oraz C B. Prosta ta przecina równoległobok w punktach F i E.

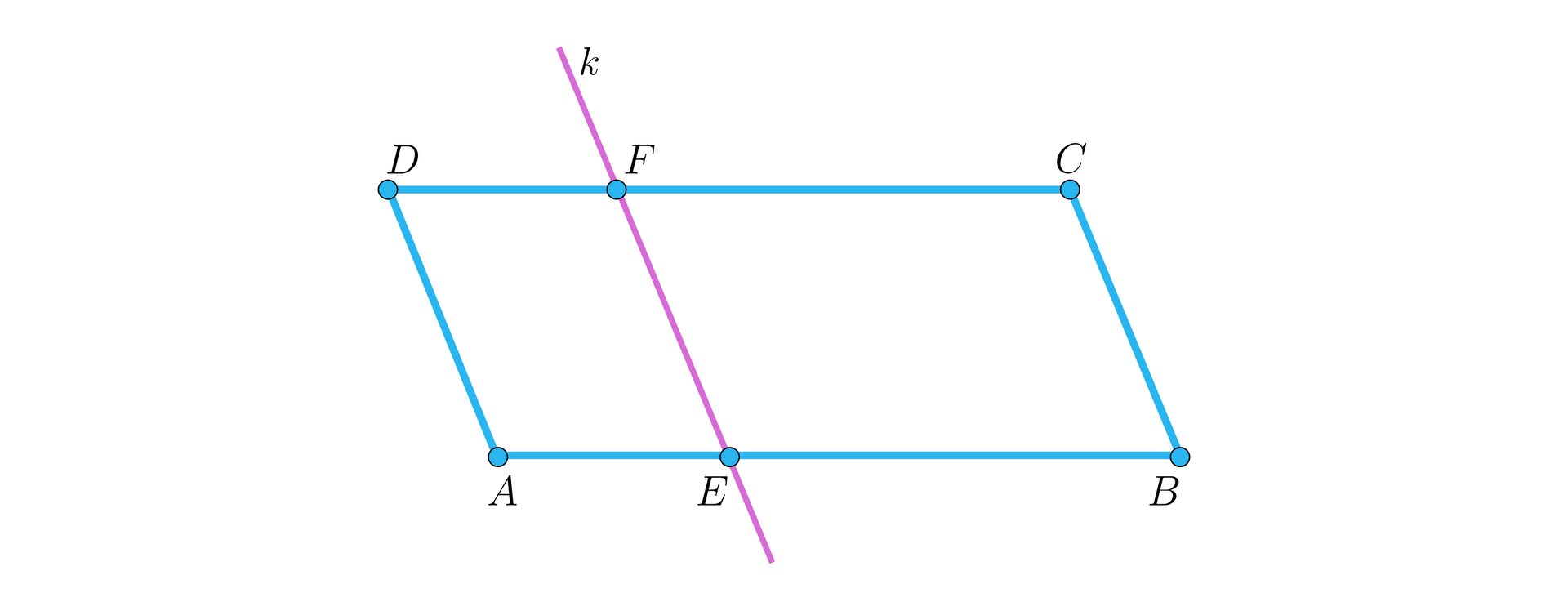
Wynika to wprost z faktu, że czworokąt $AEFD$ jest równoległobokiem.

Przecinając trójkąt równoramienny $ABC$ prostą $k$ równoległą do podstawy $AB$ tego trójkąta odcinamy z ramion $AC$ i $BC$ odcinki $DC$ i $EC$ równej długości.

RnK5Mdgrfxfij

Ilustracja przedstawia trójkąt równoramienny A B C o poziomej podstawie A B. Na rysunku przestawiono również poziomą prostą k przecinającą trójkąt w punktach D i E.

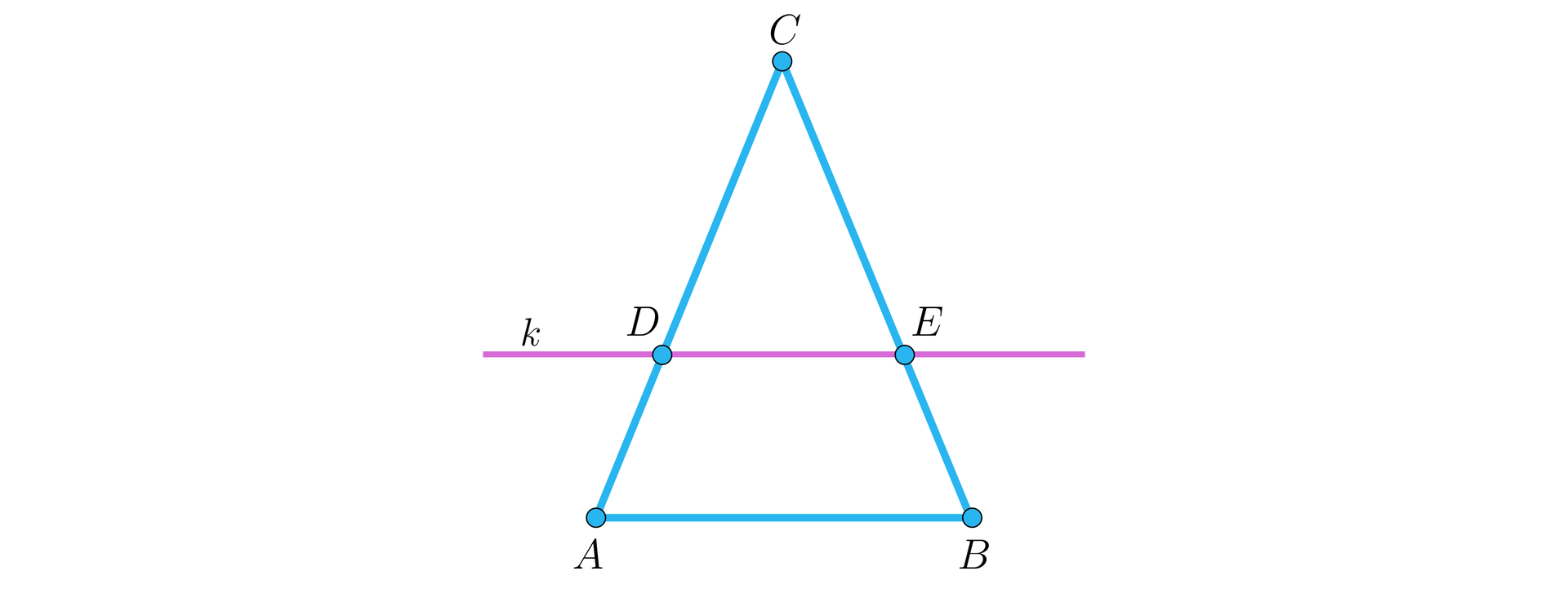
To z kolei wynika z twierdzenia o kątach odpowiadających oraz z twierdzenia o równości kątów przy podstawie trójkąta równoramiennego.

Gdy podobnie postąpimy z dowolnym trójkątem, to zazwyczaj nie otrzymamy odcinków o równych długościach. Długości otrzymanych odcinków mają jednak ciekawą własność. Własność ta wynika z twierdzenia Talesa. Jest ono, obok twierdzenia Pitagorasa, jednym z najbardziej znanych twierdzeń planimetrii. Twierdzenie to dotyczy stosunku długości odcinków, jakie otrzymujemy, przecinając ramiona kąta prostymi równoległymi. Jednym z geometrycznych zastosowań twierdzenia Talesa jest konstrukcja czwartego odcinka proporcjonalnego do trzech danych odcinków. Tę konstrukcję także omówimy.