Zależności pomiędzy funkcjami trygonometrycznymi - zadania
Ta lekcja poświęcona jest zadaniom związanym z zależnościami pomiędzy funkcjami trygonometrycznymi. Jeżeli chcesz sobie przypomnieć podstawowe wiadomości na temat trygonometrii, zajrzyj do lekcji Wprowadzenie do trygonometriiWprowadzenie do trygonometrii. Możesz sobie również przypomnieć, jak dowodzić tożsamości trygonometryczne, w tym celu zajrzyj do lekcji Obliczanie wartości funkcji trygonometrycznych. Dowodzenie tożsamości trygonometrycznych - przykładyObliczanie wartości funkcji trygonometrycznych. Dowodzenie tożsamości trygonometrycznych - przykłady.
Oblicz sinus, cosinus i tangens kąta ostrego dla przedstawionych poniżej trójkątów.
R1YovhuslZ5jh1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Rl4O3oP0UQ3uA1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R1Rym4w04qYOQ1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.R7BRLOoSA0SmX1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Na rysunku podane są długości boków trójkąta równoramiennego, którego kąt przy podstawie jest równy . Oblicz ile wynosi tego kąta.
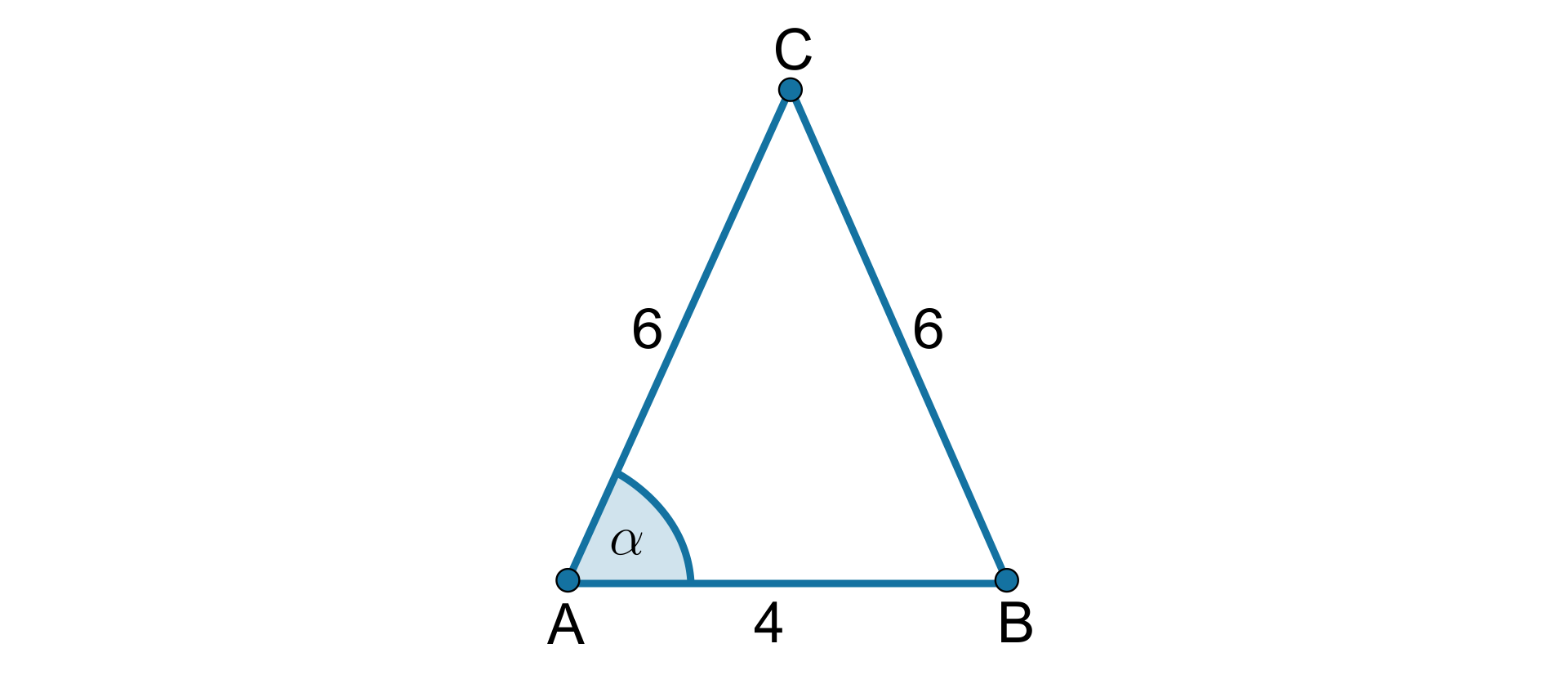
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. ,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , , ,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , , ,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , , ,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , ,
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. ,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , ,
,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , ,
,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , ,
,
1. , , , 2. , , , 3. , , , 4. , , , 5. , , , 6. , , , 7. , , , 8. , ,
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Wykaż, że:
Wykaż, że:
cos 72 ° · cos 28 ° = sin 62 ° · sin 18 ° tg 18 ° tg 54 ° = tg 36 ° tg 72 ° 3 sin 19 ° + 2 cos 71 ° sin 44 ° + 7 cos 46 ° = 40 cos 71 ° sin 44 °
W trójkącie
W rombie





