Działania na ułamkach zwykłych
5. Mnożenie ułamków zwykłych

Arkusz papieru w formacie A0 ma długość i szerokość . Arkusz w formacie A1 jest jego połową, a arkusz A2 połową tej połowy. Podobnie jest z kolejnymi arkuszami, każdy jest połową arkusza o numerze o jeden mniejszym. Aby obliczyć wymiary kolejnych arkuszy można wykorzystać mnożenie ułamków.
W tym materiale dowiesz się, w jaki sposób mnożymy ułamki zwykłe i liczby mieszane. Obliczysz również kwadraty i sześciany tych liczb.
Mnożenie ułamków właściwych
Film dostępny pod adresem /preview/resource/RZW1qY0mc3cOR
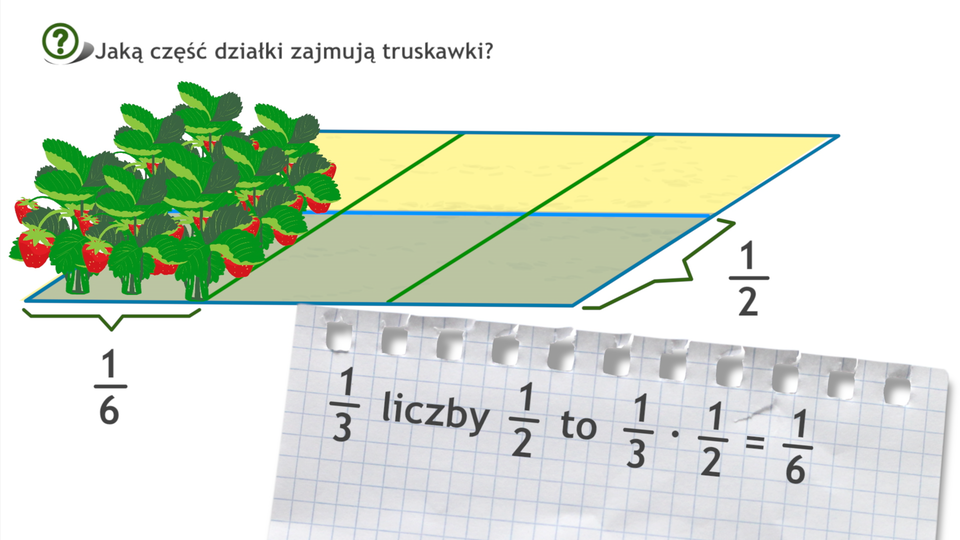
Animacja pokazująca mnożenie ułamków.
Wykonamy mnożenie dwóch ułamków.

Wynikiem mnożenia dwóch ułamków jest ułamek, którego licznik jest iloczynem liczników, a mianownik iloczynem mianowników mnożonych ułamków.
Aby pomnożyć dwa ułamki zwykłe, mnożymy licznik pierwszego ułamka przez licznik drugiego ułamka oraz mianownik pierwszego ułamka przez mianownik drugiego ułamka.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Przeciągnij i upuść.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Skróć, a następnie przeciągnij i upuść.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
f) ............
g) ............
h) ............
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4. , 5. , 6.
1. , 2. , 3. , 4. , 5. , 6.
1. , 2. , 3. , 4. , 5. , 6.
Przeciągnij i upuść.
, , ,
a) ............
b) ............
c) ............
d) ............
Czy potrafisz, nie wykonując obliczeń, uzupełnić wyniki? Przesuń odpowiednie wartości w puste pola lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
Mnożenie liczb mieszanych
Jeżeli jeden z czynników jest liczbą mieszaną lub oba są liczbami mieszanymi, zamieniamy liczby mieszane na ułamki niewłaściwe.
Pomnożymy dwie liczby mieszane, zamieniając je najpierw na ułamki niewłaściwe.
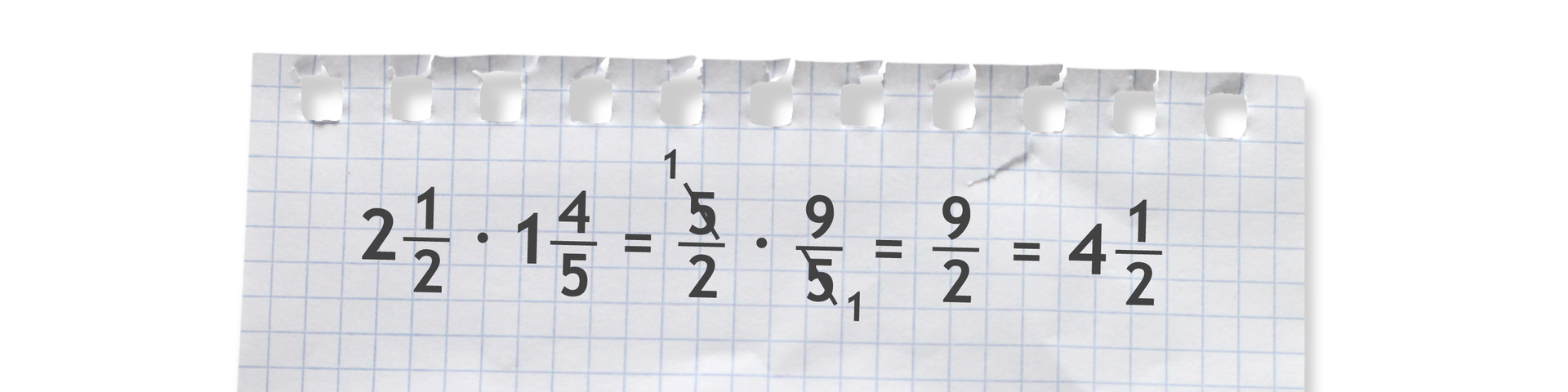
Aby pomnożyć liczby mieszane, należy zamienić je na ułamki niewłaściwe i pomnożyć otrzymane ułamki.
Połącz w pary.
<math><mn>3</mn><mfrac><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></mfrac><mo> &CenterDot; <mn>1</mn></mo><mfrac><mrow><mn>3</mn></mrow><mrow><mn>4</mn></mrow></mfrac></math>, <math><mn>1</mn><mfrac><mrow><mn>1</mn></mrow><mrow><mn>3</mn></mrow></mfrac><mo> &CenterDot; <mn>1</mn></mo><mfrac><mrow><mn>3</mn></mrow><mrow><mn>5</mn></mrow></mfrac></math>, <math><mn>1</mn><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo> &CenterDot; <mn>1</mn></mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>10</mn></mrow></mfrac></math>, <math><mn>2</mn><mfrac><mrow><mn>1</mn></mrow><mrow><mn>4</mn></mrow></mfrac><mo> &CenterDot; <mn>2</mn></mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac></math>
1. , 2. , 3. , 4. , 5. , 6. , 7.
1. , 2. , 3. , 4. , 5. , 6. , 7.
1. , 2. , 3. , 4. , 5. , 6. , 7.
1. , 2. , 3. , 4. , 5. , 6. , 7.
1. , 2. , 3. , 4. , 5. , 6. , 7.
1. , 2. , 3. , 4. , 5. , 6. , 7.
Przeciągnij i upuść.
, , , , , , , , ,
a) ............ b) ............
c) ............ d) ............
e) ............ f) ............
g) ............ h) ............
Kwadraty i sześciany ułamków zwykłych
Kwadrat liczby to iloczyn dwóch jednakowych czynników, np.
Sześcian liczby to iloczyn trzech jednakowych czynników, np.
Kwadraty i sześciany ułamków obliczamy podobnie, jak kwadraty i sześciany liczb naturalnych.
Aby podnieść do kwadratu ułamek zwykły, należy ten ułamek pomnożyć przez siebie.
Aby obliczyć kwadrat liczby mieszanej, należy najpierw zamienić tę liczbę na ułamek niewłaściwy.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.