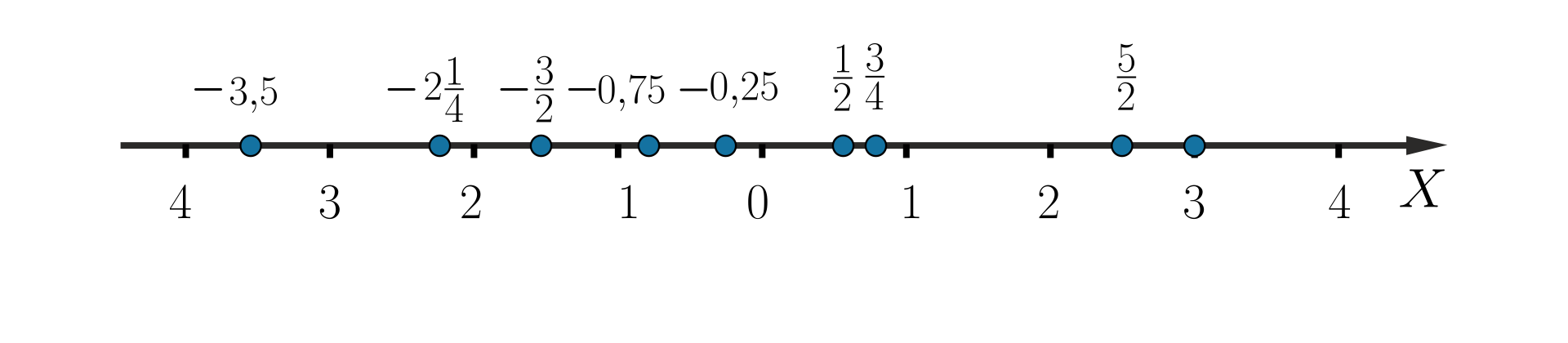Działania na liczbach wymiernych
3. Porównywanie liczb wymiernych 1

Najkrótszym dystansem na zawodach lekkoatletycznych na otwartym stadionie jest bieg na metrów, nazywany klasycznym biegiem sprinterskim. Rekordzistów świata na tym dystansie nazywa się często najszybszymi mężczyznami lub najszybszymi kobietami świata.
Według danych na dzień roku najszybciej ten dystans pokonali:
Usain Bolt – (Jamajka)
Tyson Gay – (USA)
Yohan Blake – (Jamajka)
Asafa Powell – (Jamajka)
Justin Gatlin – (USA).
Z powyższego zestawienia wynika, że rekordzistą świata w biegu na metrów w był Usain Bolt.
W życiu codziennym ważną umiejętnością jest porównywanie wielkości. Porównujemy na przykład ceny w sklepach, wzrost ludzi, odległości między miastami. Porównywanie sprowadza się do odpowiedzi na pytanie: Która z liczb, wyrażających daną wielkość, jest mniejsza, a która większa?
W tym materiale będziemy porównywać liczby wymierne.
Aby porównać liczby wymierne, czyli określić, czy są równe lub która z nich jest większa, a która mniejsza, możemy przedstawić je na osi liczbowej.
Zaznaczmy na osi liczbowej dowolną liczbę ujemną i dowolną liczbę dodatnią.
R8LBzTWmjIDt61 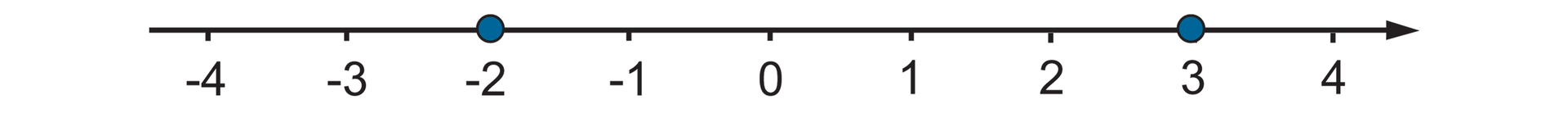 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Oczywiste jest, że każda liczba dodatnia jest większa od liczby ujemnej.
Zaznaczmy na osi liczbowej dwie dowolne liczby dodatnie.
RSPzetwATHISo1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Oczywiste jest również, że z dwóch liczb dodatnich większa jest ta, która znajduje się dalej od na osi liczbowej.
Zaznaczmy na osi liczbowej dwie dowolne liczby ujemne.
RT8eHc82IwbTs1  Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.Z dwóch liczb ujemnych większa jest ta, która leży bliżej na osi liczbowej.
Porównajmy liczby i .
W tym celu zaznaczymy je na osi liczbowej.

Bliżej znajduje się liczba , zatem jest ona większa od liczby .
Pamiętamy, że odległość liczby od na osi liczbowej nazywa się wartością bezwzględną.
Mamy
ponieważ
Możemy zatem powiedzieć, że z dwóch liczb ujemnych większa jest ta, której wartość bezwzględna jest mniejsza.
Z dwóch liczb ujemnych większa jest ta, której wartość bezwzględna jest mniejsza.
Zaznacz na osi liczbowej podane liczby, a następnie uporządkuj je od najmniejszej do największej.
, , , , , , , ,
Pod jakimi literami kryją się dane ułamki?
, , , , , .

Uporządkuj liczby rosnąco.
W miejsce kropek wstaw taką liczbę, aby otrzymać nierówność prawdziwą.
W miejsce kropek wstaw taką liczbę, aby otrzymać nierówność prawdziwą.
- Ułamek jest większy od i mniejszy od .
- Liczba jest mniejsza od liczby .
- Najmniejszą liczbą całkowitą, która jest większa od liczby jest .
- Największą liczbą całkowitą, która jest mniejsza od liczby jest .
Podaj
a. dwie liczby całkowite ujemne i dwie liczby całkowite dodatnie, które są mniejsze od i jednocześnie większe od ,
b. taką liczbę całkowitą , która spełnia warunek ,
c. dwie dowolne liczby wymierne, które są większe od i mniejsze od ,
d. trzy dowolne liczby, które są większe od i jednocześnie mniejsze od .
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.