12. Energia dla każdego. Podsumowanie
Korzystając z tego materiału powtórzysz pojęcia i definicje takich wielkości fizycznych, jak: praca, moc, energia mechaniczna, energia potencjalna i energia kinetyczna. Przypomnisz sobie też zasadę zachowania energii mechanicznej.
Praca

Znaczenie słowa praca w języku potocznym nie pokrywa się z jego znaczeniem w języku fizyki.
W języku fizyki praca to zdefiniowana wielkość, będąca iloczynem siły i przemieszczenia , jeśli kierunki siły i przemieszczenia są takie same; w takiej sytuacji możemy ją wyrazić wzorem:
Jednostką pracy jest dżul, 1 J jest równy pracy wykonanej przez siłę na drodze :
Praca siły prostopadłej do przemieszczenia ma wartość zero.
Moc
Moc informuje nas, jaka jest szybkość wykonywanej pracy lub inaczej – ile pracy wykonywano w jednostce czasu. Moc jest równa ilorazowi pracy i czasu , w którym ta praca została wykonana:
Jeżeli praca była wykonywana ze zmienną szybkością, to otrzymamy wartość średniej mocy.
Jednostką mocy w układzie SI jest wat. Urządzenie ma moc wata, jeśli w ciągu sekundy wykonuje pracę dżula:
Energia mechaniczna

Energię posiada ciało lub układ ciał, które mają zdolność do wykonania pracy. Może ona występować w różnych formach, np. energia elektryczna, energia cieplna, energia chemiczna, energia mechaniczna.
Jednostką energii jest dżul.
Energia ciała może się zmieniać. Gdy ciało wykonuje pracę, jego energia maleje, a podczas gdy siły zewnętrzne wykonują pracę nad ciałem – jego energia wzrasta o wartość wykonanej pracy.
Energia mechaniczna jest sumą energii kinetycznej i potencjalnej: .
Energia potencjalna

Energia potencjalna jest jedną z form energii mechanicznej. Posiadają ją ciała, które oddziałują ze sobą (przyciągają się lub odpychają), a jej wartość zależy od położenia tych ciał względem siebie. Jeśli między ciałami działa siła grawitacji – mówimy o energii potencjalnej grawitacji.
Energia potencjalna grawitacji to energia układu ciał oddziałujących siłami grawitacyjnymi. Wartość tej energii zależy od masy ciał oraz od odległości między nimi; rośnie, gdy zwiększa się odległość między oddziałującymi ciałami oraz jest większa w przypadku ciał o większej masie.
Wartość grawitacyjnej energii potencjalnej dla ciała o masie znajdującego się w pobliżu powierzchni Ziemi obliczamy ze wzoru: , gdzie oznacza wysokość ponad pewien umownie przyjęty poziom (gdzie energia potencjalna ciała jest równa zero).
R6YgKJNZPftiC 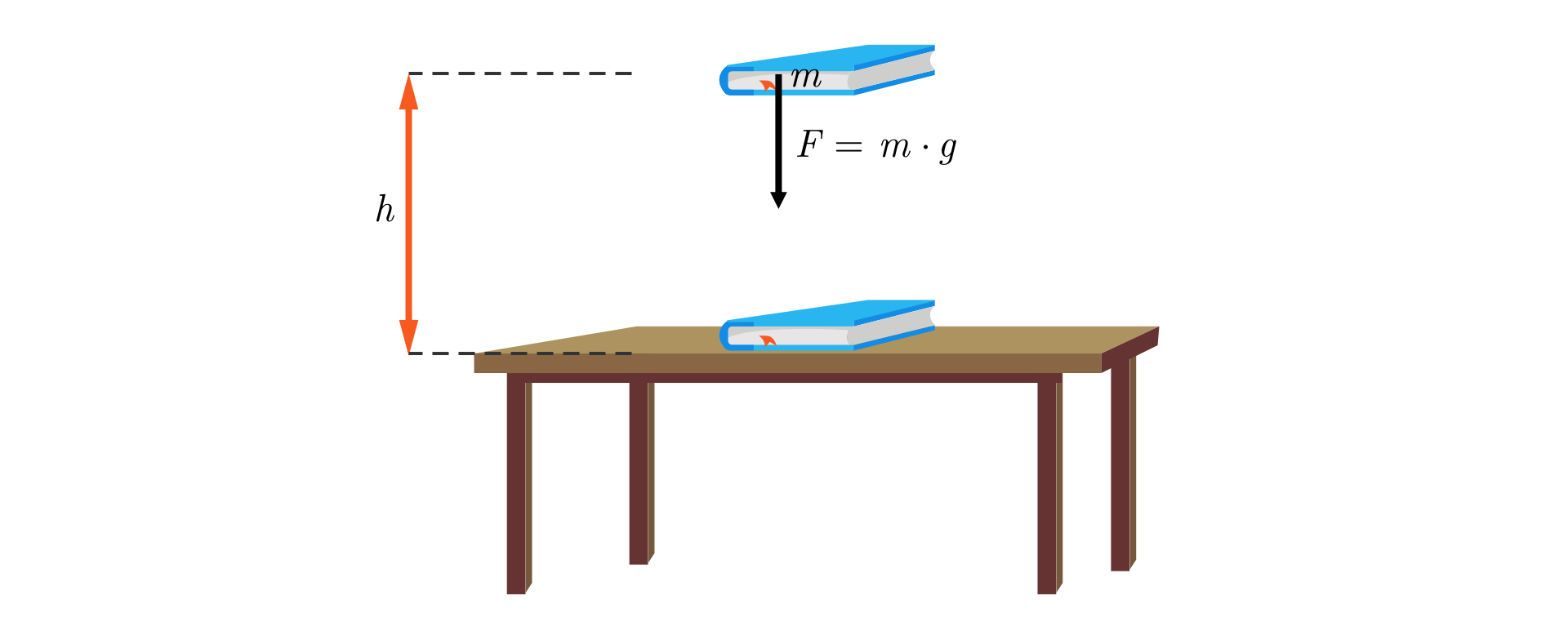 Ile energii zyska ciało o masie po podniesieniu go na wysokość nad powierzchnię stołu?Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.
Ile energii zyska ciało o masie po podniesieniu go na wysokość nad powierzchnię stołu?Źródło: GroMar Sp. z o.o., licencja: CC BY-SA 3.0.Wartość energii potencjalnej grawitacji zależy od wyboru poziomu, względem którego ją obliczamy. Ponieważ oddziaływanie Ziemi słabnie ze wzrostem odległości od niej, zależność ta jest prawdziwa blisko powierzchni Ziemi.
Przyrost energii potencjalnej grawitacji nie zależy od wyboru poziomu odniesienia i jest wprost proporcjonalny do masy ciała i zmiany wysokości.
Energia potencjalna sprężystości to energia zgromadzona w ciałach odkształconych sprężyście. Odkształconych to znaczy rozciągniętych, ściśniętych, wygiętych lub skręconych. Wartość tej energii jest wprost proporcjonalna do kwadratu odkształcenia oraz zależy od właściwości sprężystych odkształcanego ciała. Zawsze jest równa pracy, jaką trzeba włożyć, aby odkształcić ciało.
Energia potencjalna sprężystości rozciągniętej sprężyny wyraża się wzorem:
gdzie x oznacza wielkość rozciągnięcia sprężyny, a k‑jest to tzw. współczynnik sprężystości sprężyny informujący o tym, ile niutonów siły należy użyć, aby daną sprężynę rozciągnąć o 1 metr.
Energia kinetyczna

Energia kinetyczna to jedna z form energii mechanicznej. Posiadają ją ciała będące w ruchu i zależy ona od masy ciała oraz wartości jego prędkości.
Energia kinetyczna ciała równa jest pracy, jaką trzeba wykonać, aby ciało o masie m rozpędzić do prędkości (lub zatrzymać ciało będące w ruchu).
Wartość energii kinetycznej ciała równa jest iloczynowi połowy masy ciała i kwadratu wartości prędkości ciała:
Energia kinetyczna ciała jest wprost proporcjonalna do masy ciała. Oznacza to, że na przykład trzykrotne zwiększenie masy ciała powoduje trzykrotny wzrost jego energii kinetycznej (przy niezmienionej prędkości).
Energia kinetyczna ciała jest proporcjonalna do kwadratu prędkości, co oznacza, że na przykład trzykrotny wzrost prędkości powoduje aż dziewięciokrotny wzrost jego energii kinetycznej (przy stałej masie ciała).
Wartość energii kinetycznej zależy od układu odniesienia, ponieważ prędkość ciała zależy od układu odniesienia.
Ciała o różnych masach mogą mieć takie same energie kinetyczne, jeśli mają różne prędkości. Ciało o masie np. 100 razy mniejszej osiągnie taką samą energię kinetyczną jak ciało masywniejsze, jeśli jego prędkość będzie 10 razy większa.
Zasada zachowania energii
Zasada zachowania energii mechanicznej ma charakter empiryczny, to znaczy, że została sformułowana jako wniosek z bardzo wielu doświadczeń.
Zasada zachowania energii mechanicznej głosi, że jeżeli siły zewnętrzne nie wykonują pracy nad układem ciał i na składniki układu nie działają siły tarcia lub oporu ośrodka, to energia mechaniczna układu pozostaje stała. To znaczy, że energie kinetyczna i potencjalna składników układu mogą się zmieniać, ale ich suma pozostaje niezmieniona. Można to zapisać równaniem:
Zasada zachowania energii mechanicznej ma duże znaczenie praktyczne, ponieważ pozwala w łatwy i prosty sposób obliczyć lub przynajmniej oszacować niektóre wielkości opisujące stan układu ciał w różnych procesach.
Aby przypomnieć sobie więcej szczegółów, zajrzyj do materiałów: