3. Weryfikacja rozwiązania zadania tekstowego

RGcEzeqJ1un8Z

Matematycy wymyślają wiele podchwytliwych zadań, aby pokazać, że każde rozwiązanie wymaga przemyślenia. Czasem to, co wydaje się nam bezsensowne ma głęboki sens i odwrotnie – proste z pozoru zagadnienie może być trudne do zinterpretowania.

Poniżej jest przykład zagadki, która pokazuje, że treść zadania należy najpierw dobrze przeczytać, nim stwierdzi się, że problem jest nie do rozwiązania.

Na stole leżą dwie monety. Łączna ich wartość to $7$ złotych. Pierwsza z nich nie jest jednak dwuzłotówką. Czy to możliwe?

Po przeanalizowaniu zadania, zapewne dasz poprawną odpowiedź – skoro pierwsza moneta nie jest dwuzłotówką, to musi być nią druga moneta.

RNMFbt3tZER8U

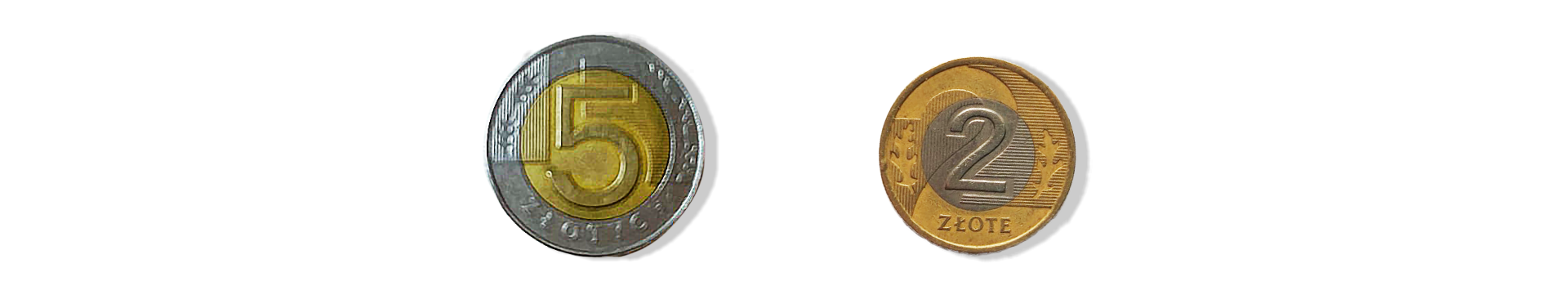
Ilustracja przedstawia rewers monety pięciozłotowej i dwuzłotowej. — Źródło: dostępny w internecie: Wikipedia.org, licencja: CC BY 3.0.

Czyli na stole leży pięciozłotówka i dwuzłotówka. Wystarczyło tylko zauważyć sformułowanie „pierwsza z nich” i dalej już problem staje się banalny.

Podchwytliwe zadania nasuwają nam pytania: czy każde zadanie matematyczne musi mieć rozwiązanie? Czy zawsze trzeba ocenić poprawność rozwiązania? Ile rozwiązań może mieć zadanie? Na te pytania uzyskasz odpowiedź, zapoznając się z poniższym materiałem.

Na ogół matematyczne zadanie tekstowezadanie tekstowezadanie tekstowe rozwiązuje się według następującego schematu:

uważne przeczytanie i zrozumienie zadania,
ułożenie i realizacja planu rozwiązania zadania,
sprawdzenie wyniku,
refleksja nad rozwiązaniem.

Zrozumienie treści zadania to najtrudniejszy element rozwiązania. Trzeba bowiem dokonać selekcji – co jest dane, czego szukamy, czego nam brakuje. Po ustaleniu celu (czyli tego, czego szukamy), trzeba określić, jakie warunki musi spełniać rozwiązanie.

Przykład 1

Paweł ma $13$ kur, $18$ kaczek i kilka owiec – razem $29$ zwierząt. Ile ma owiec?

W zadaniu od razu mamy określone, że szukamy ile owiec ma Paweł. Zatem liczba, którą otrzymamy w obliczeniach musi być liczbą całkowitą nieujemną.

Brakuje nam informacji, ile łącznie pozostałych zwierząt ma Paweł. I od tego zaczynamy rozwiązanie zadania.

Obliczamy, ile łącznie kur i kaczek ma Paweł.

13 + 18 = 31

Teraz od liczby wszystkich zwierząt trzeba odjąć łączną liczbę kur i kaczek.

29 - 31 = - 2

Otrzymaliśmy liczbę ujemną.

Choć wykonaliśmy poprawne obliczenia, otrzymana liczba nie spełnia warunków zadania – ilość owiec nie może wyrażać się liczbą ujemną. Po zweryfikowaniu wyniku stwierdzamy, że zadanie nie ma rozwiązania.

Planując rozwiązanie zadania, należy dokładnie przeanalizować treść zadania, bo jak wynika z powyższego przykładu, zadanie może nie mieć rozwiązania. Zatem warto zadać sobie od razu pytanie – czy jest możliwe, aby istniało rozwiązanie danego zadania.

Przykład 2

Paweł i Gaweł mają łącznie $26$ lat. Paweł mieszka w Krakowie, a Gaweł w Łańcucie. Ile lat ma Gaweł?

Po przeczytaniu zadania, od razu orientujemy się, że w zadaniu jest za mało danych, aby określić ile lat ma Gaweł. Nie staramy się więc poszukiwać wyniku, gdyż zadanie nie ma rozwiązania.

W niektórych zadaniach trzeba zapytać: od jakich danych zacząć, które są najbardziej użyteczne? Jeśli jednak wykorzystanie tych danych nie wystarczy do znalezienia wyniku, warto zastanowić się jakiego rodzaju zadanie mamy rozwiązać.

Czy jest to zadanie z jedną niewiadomą, a może trzeba znaleźć kilka niewiadomych. Jeśli uznamy, że jednak szukamy co najmniej dwóch wielkości, trzeba zastanowić się, jak zapisać zależności między tymi danymi, którą najpierw wyznaczyć.

Przykład 3

Paweł chce kupić kury i kaczki, łącznie $6$ ptaków. Chce aby kur było więcej niż kaczek. Ile kur i ile kaczek powinien kupić?

W zadaniu mamy dwie niewiadome – liczbę kur i liczbę kaczek.

Oznaczmy jedną z niewiadomych przez $x$ . Niech to będzie liczba kaczek. Wtedy liczba kur to $6 - x$ .

Teraz nie bardzo wiadomo co zrobić, bo już nie mamy w zadaniu więcej danych.

Zastanówmy się więc, co wynika z treści zadania.

Ponieważ wszystkich ptaków jest sześć, to liczba $x$ nie może być większa od $6$ . Ponadto jest to liczba naturalna.

Zatem $x$ to $0$ , $1$ , $2$ , $3$ , $4$ , $5$ lub $6$ i $x < 6 - x$ , bo kur jest więcej niż kaczek. Rozważamy wszystkie przypadki.


Liczba kaczek $x$	Liczba kur $6 - x$	Czy $x < 6 - x$ ?	Czy $x$ spełnia warunki zadania?
$0$	$6$	tak	tak
$1$	$5$	tak	tak
$2$	$4$	tak	tak
$3$	$3$	nie	nie
$4$	$2$	nie	nie
$5$	$1$	nie	nie
$6$	$0$	nie	nie

Zauważmy, że tylko liczby $0$ , $1$ , $2$ mogą określać liczbę kaczek. W treści zadania zapisane jest, że Paweł chce kupić kaczki i kury, więc domyślamy się, że chce kupić co najmniej jedną kaczkę.

Ostatecznie wybieramy tylko liczby $1$ i $2$ .

Wtedy
$6 - 1 = 5$ ,
$6 - 2 = 4$ .

Zadanie ma dwa rozwiązania: Paweł powinien kupić $1$ kaczkę i $5$ kur lub $2$ kaczki i $4$ kury.

Realizując ułożony wcześniej plan rozwiązania zadania nie zawsze można sprawdzić, czy wykonane obliczenia prowadzą do sensownego wyniku. Zatem po wyznaczeniu wszystkich niewiadomych, trzeba sprawdzić, czy wszystkie liczby spełniają warunki zadania.

Przykład 4

Ojciec ma $28$ lat, a syn ma $3$ lata. Za ile lat ojciec będzie $6$ razy starszy od syna?

Zakładamy, że zadanie ma rozwiązanie i oznaczamy przez $x$ szukaną liczbę lat.

Analizę zadania zapisujemy w tabelce.


Wiek	Obecnie	Za $x$ lat
Wiek ojca	$28$	$28 + x$
Wiek syna	$3$	$3 + x$

Układamy odpowiednie równanie.

28 + x = 6 (3 + x)

Zgadujemy, że $x = 2$ . Jednak to nie jest ostateczna odpowiedź do zadania. Może jest więcej liczb spełniających to równanie? A może nawet nieskończenie wiele!

Pozostaje nam więc rozwiązać zapisane równanie. Zastosujemy metodę równań równoważnych.

28 + x = 6 (3 + x)

28 + x = 18 + 6 x - 18 - x

28 + x - 18 - x = 18 + 6 x - 18 - x

10 = 5 x : 5

x = 2

Otrzymaliśmy taką samą liczbę, którą wytypowaliśmy na początku jako rozwiązanie zadania. Jednak teraz mamy pewność, że jest to jedyna liczba spełniająca równanie.

Aby upewnić się, że jest ona też rozwiązaniem zadania, sprawdzamy warunek wynikający z treści zadania.

Za $2$ lata ojciec będzie miał $28 + 2 = 30$ lat, a syn $3 + 2 = 5$ lat.

30 : 5 = 6

Znaleziona liczba spełnia warunki zadania, podajemy odpowiedź.

Odpowiedź:
Za $2$ lata ojciec będzie $6$ razy starszy od syna.

Niekiedy zadanie łatwiej jest rozwiązać sporządzając odpowiedni rysunek. Wtedy też, po ustaleniu odpowiedzi warto sprawdzić sensowność rozwiązania.

Przykład 5

Pani Iza potrzebuje $2$ godzin, aby zerwać wszystkie jabłka z jabłonki. Pani Ela potrzebuje $3$ godzin, aby zerwać wszystkie jabłka z tej jabłonki. W ciągu ilu godzin panie oberwą jabłka z jabłonki pracując wspólnie?

Na podstawie treści zadania od razu ustalamy, że szukana liczba musi być mniejsza od $2$ .

Zauważmy, że najmniejszą wspólną wielokrotnością liczb $2$ i $3$ jest $6$ . Określimy więc, z ilu jabłonek zerwie jabłka każda z pań w ciągu $6$ godzin.

Pani Iza

R167BItZFP89c

Ilustracja przedstawia 3 zdjęcia jabłonek. Każde z trzech zdjęć zostało podpisane „2 godziny”. Poniżej klamra obejmująca zdjęcia z podpisami wraz z zapisem „6 godzin”. — Źródło: dostępny w internecie: Pixabay.com, licencja: CC BY 3.0.

$2$ godziny – $1$ jabłonka
$6$ godzin – $3$ jabłonki

Pani Ela

RvKr2Qmep37Xh

Ilustracja przedstawia 2 zdjęcia jabłonek. Każde z dwóch zdjęć zostało podpisane „3 godziny”. Poniżej klamra obejmująca zdjęcia z podpisami wraz z zapisem „6 godzin”. — Źródło: dostępny w internecie: Pixabay.com, licencja: CC BY 3.0.

$3$ godziny – $1$ jabłonka

$6$ godzin – $2$ jabłonki

RpvmJzwkbFKvK

Ilustracja, można ją podzielić na dwie części. Lewą część podpisano Pani Iza, a prawą część Pani Ela. Na prawej części znajdują się trzy zdjęcia jabłonek, a na lewej dwa zdjęcia jabłonek. Zatem razem znajduje się pięć jabłonek na ilustracji. — Źródło: dostępny w internecie: Pixabay.com, licencja: CC BY 3.0.

Ustaliliśmy, że w ciągu $6$ godzin panie pracując razem, zerwą jabłka z $5$ jabłonek.

$5$ jabłonek – $6$ godzin

$1$ jabłonka – $\frac{6}{5}$ godziny

Sprawdzamy, czy nasze rozumowanie doprowadziło nas do poprawnej odpowiedzi.

Pani Iza na oberwanie jabłek potrzebuje $2$ godzin, więc w ciągu godziny wykona $\frac{1}{2}$ całej pracy. Pani Ela natomiast w ciągu godziny wykona $\frac{1}{3}$ całej pracy.

Zatem w ciągu godziny wykonają wspólnie $\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$ całej pracy.

Czyli w ciągu $\frac{6}{5}$ godziny wykonają $\frac{5}{6} \cdot \frac{6}{5} = 1$ , czyli całą pracę.

Nasze rozwiązanie jest poprawne.

Odpowiedź:
Panie pracując razem oberwą jabłka z jednej jabłonki w ciągu $\frac{6}{5}$ godziny.

Na koniec – zagadka.

Przykład 6

Od podwojonej liczby $a$ odjęto $6$ i wynik podzielono przez $2$ . Następnie do otrzymanego wyniku dodano $4$ , odjęto $a$ i otrzymano $1$ . Ile jest równa liczba $a$ ?

Treść zadania zilustrujemy grafem.

R6oQt6eUNUuAq

Ilustracja przedstawia graf. Zaczynając od lewej strony: z pierwszego pola prowadzi strzałka z podpisem razy dwa do drugiego pola.
Z drugiego pola poprowadzono strzałkę z podpisem minus sześć do trzeciego pola. Z trzeciego pola poprowadzono strzałkę z podpisem podzielić na dwa do czwartego pola.
Z czwartego pola poprowadzono strzałkę z podpisem plus cztery do piątego pola. Z piątego pola do szóstego pola poprowadzono strzałkę z popisem minus a. W ostatnie pole wpisano cyfrę jeden. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Uzupełnimy graf metodą działań odwrotnych, wpisując odpowiednie liczby lub wyrażenia.

R15iYuDaEi2Av

Okazuje się, że dla każdej liczby rzeczywistej, po wykonaniu wskazanych w zadaniu działań, w wyniku otrzymamy $1$ . Zatem szukaną liczbą $a$ może być każda liczba rzeczywista.

Jeśli mamy wątpliwości, możemy sprawdzić uzyskany wynik dla kilku wybranych liczb (ale pamiętajmy, że takie sprawdzenie nie jest dowodem, że uzyskany wynik jest poprawny).

Prezentacja multimedialna

Polecenie 1

Zapoznaj się z prezentacją, w której zamieszczone są przykłady zadań niestandardowych (czyli „podchwytliwych” albo takich, które celowo są źle sformułowane).

Zweryfikuj najpierw samodzielnie otrzymane w tych zadaniach wyniki, a następnie porównaj z odpowiedzią.

RUFh18HR2SizK

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R1WJLf303HRQT

R1137yaZyqa0W

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RHcHuOh68fj7j

R9Kr1K0zoMH5A

Ilustracja nawiązująca do treści materiału — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Rtm3GhqLcpnJb

R62zrMZshACSl

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RD4dBPkxnXiDA

RxRz6zAZ7G2Zk

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R54JC1oBFUWHj

R1K7CxQkNRpeU

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

R184TTOnBYOI7

RYMhEWMMm0jX6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

RBZNeNeLmRWBk

Transkrypcjaazurewhite

RDmbKURGBq0VA

RHs5CD57NC0LN

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

ReMR9ucsfankm

Transkrypcjaazurewhite

R6RuFE1CJ0LYz

R1bQ3q7RkwFuv

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Transkrypcjaazurewhite

Slajd pierwszy

Na pewno nie raz zdarzyło ci się złapać na haczyk zadania matematycznego.

Aby uniknąć w przyszłości takich sytuacji, zapoznaj się z zadaniami przedstawionymi w prezentacji. Niektóre z tych zadań mają rozwiązania, ale nie zawsze sensowne. Inne rozwiązań nie mają, choć można je rozwiązać.

Skomplikowane, prawda?

Na planszy przedstawiono ucznia próbującego rozwiązać zadanie. Wokół niego znajdują się pogniecione w kulkę kartki. Na dole planszy znajduje się tytuł Przykłady zadań niestandardowych.

Slajd drugi

Pokażemy teraz, jak istotne jest sprawdzenie poprawności otrzymanego wyniku po rozwiązaniu zadania.

Przykład pierwszy

W parku wzdłuż alejki długości stu dziesięciu metrów, co dziesięć metrów ustawiono ławki.

Pierwszą ławkę ustawiono na początku alejki, a drugą na końcu. Ile ławek ustawiono?

Zadanie wydaje się dość proste do rozwiązania. Ponieważ podana jest długość alejki i informacja, że ławki stoją co dziesięć metrów, zatem sto dziesięć podzielić przez dziesięć to jedenaście i mamy gotową odpowiedź.

Czy to jest na pewno dobra odpowiedź? Przecież na początku alejki stoi ławka i na końcu też. Więc może trzeba dodać te dwie ławki do już wyznaczonych. Otrzymaliśmy teraz trzynaście ławek. Mamy dwie odpowiedzi. Którą wybrać? Jak sprawdzić, który wynik jest poprawny?

Slajd trzeci

Najprościej będzie wykonać pomocniczy rysunek.

Narysowano oś. Nad osią zapisano liczby naturalne od jednego do dwunastu. Pod osią zapisano liczby od dziesięciu do stu dziesięciu wzrastające co dziesięć. Następnie zaznaczano kolejno pionowymi kreskami kolejne ławki zaczynając od początku alejki.

Wówczas okazuje się, że ustawiono dwanaście ławek, a nie tak, jak przypuszczaliśmy jedenaście lub trzynaście! Dobrze, że zweryfikowaliśmy otrzymane wyniki!

Slajd czwarty

Przykład drugi

Sześć worków węgla waży łącznie sto pięćdziesiąt kilogramów. Ile waży łącznie dziewięć takich worków?

Tym razem zadanie wydaje się dość proste.

Trzeba wykonać dzielenie. Tylko co przez co podzielić? Zacznijmy od pierwszego sposoby rozwiązania. Najpierw podzielimy sześć przez sto pięćdziesiąt i wynik pomnożymy przez dziewięć – ponieważ mamy obliczyć wagę dziewięciu takich worków węgla. Otrzymujemy wówczas $\frac{54}{150}$ . Zatem $\frac{54}{150} < 150$ . Wówczas $\frac{54}{150} kg < 150 kg$ . Oceniamy, czy otrzymany wynik jest prawdopodobny. Dziewięć worków węgla powinno ważyć więcej niż sześć worków węgla. A my ustaliliśmy, że dziewięć worków węgla waży mniej niż sześć takich worków. Zatem nasze rozumowanie było niepoprawne.

Slajd piąty

Rozważmy drugi sposób rozwiązania. Tym razem dzielimy sto pięćdziesiąt przez sześć i mnożymy przez dziewięć, czyli $\frac{150}{6} \cdot 9 = \frac{150}{2} \cdot 3 = 225$ . Stąd $225 > 150$ , czyli $225 kg > 150 kg$ .

Wydaje się, że teraz już jest dobry wynik, bo dwieście dwadzieścia pięć to więcej niż sto pięćdziesiąt. Zatem dziewięć worków węgla waży więcej niż sześć takich worków.

Slajd szósty

Ale czy na pewno uzyskaliśmy poprawny wynik? Przeanalizujemy jeszcze raz całą sytuację.

Możemy również ułożyć następującą proporcję. Jeśli sześć worków węgla waży sto pięćdziesiąt kilogramów, to osiemnaście takich worków waży trzy razy tyle, czyli czterysta pięćdziesiąt kilogramów. A dziewięć worków węgla waży o połowę mniej, czyli dwieście dwadzieścia pięć kilogramów., czyli $450 kg : 2 = 225 kg$ .

Czyli nasze poprzednie obliczenia były poprawne. Dziewięć worków węgla waży dwieście dwadzieścia pięć kilogramów.

Slajd siódmy

Rozwiążemy następujące zadanie.

Ludwik rozwiązał w poniedziałek dwanaście zadań z matematyki.

Ile takich zadań rozwiąże Ludwik w ciągu tygodnia?

Tydzień ma siedem dni. Skoro jednego dnia Ludwik rozwiązuje dwanaście zadań, to w ciągu tygodnia rozwiąże siedem razy więcej zadań, czyli osiemdziesiąt cztery zadania.

Aby sprawdzić, czy uzyskaliśmy poprawny wynik, popatrzmy jeszcze raz na treść zadania. Co z niej wynika? Tylko tyle, że Ludwik w poniedziałek rozwiązał dwanaście zadań. Natomiast nie wiemy, czy każdego innego dnia rozwiązywał po tyle samo zadań. A może w niedzielę pojechał do babci i nie rozwiązał żadnego zadania?

To zadanie nie ma doprecyzowanej treści, nie ma więc rozwiązania.

Slajd ósmy

Przykład czwarty

Pan Grzegorz wybrał się na dwudniową pieszą wycieczkę. Miał do pokonania czterysta dwadzieścia pięć kilometrów. Pierwszego dnia przeszedł o piętnaście kilometrów więcej niż drugiego dnia. Ile kilometrów przebył pan Grzegorz drugiego dnia?

Nauczeni doświadczeniem, sprawdzamy, czy w zadaniu zamieszczone są wszystkie potrzebne dane.

Slajd dziewiąty

Najprościej będzie ułożyć i rozwiązać odpowiednie równanie. Oznaczmy iks jako liczbę kilometrów jaką przeszedł Pan Grzegorz pierwszego dnia. Wówczas iks plus piętnaście to ilość kilometrów jaką przeszedł Pan Grzegorz drugiego dnia. Zatem $x + x + 15 = 425$ , $2 x = 425 - 15$ , $2 x = 410$ , $x = 205$ . Ustaliliśmy, że pan Grzegorz pierwszego dnia przeszedł dwieście pięć kilometrów. Wówczas $205 km + 15 km = 220 km$ .

Drugiego dnia przeszedł o piętnaście kilometrów więcej, zatem dwieście dwadzieścia kilometrów. I w ten sposób mamy gotową odpowiedź. Ale czy na pewno? Czy jest możliwe, aby jednego dnia pokonać pieszo dwieście dwadzieścia kilometrów? To zadanie nie ma sensu z praktycznego punktu widzenia.

Slajd dziesiąty

W ostatnim przykładzie mamy do ustalenia ile wolnych miejsc zostało w ostatnim z pokoi, w których lokowano kolonistów.

O to treść zadania. Stu czterdziestu kolonistów rozlokowano w kolejnych czterdziestu pięciu trzyosobowych pokojach. Ile wolnych miejsc zostało w ostatnim pokoju?

Slajd jedenasty

Obliczamy najpierw ilu kolonistów rozlokowano w trzyosobowych pokojach. $45 \cdot 3 = 135$ .

Teraz od liczby wszystkich kolonistów odejmujemy liczbę rozlokowanych kolonistów. $140 - 135 = 5$ . Wnioskujemy, że w ostatnim pokoju zostało pięć wolnych miejsc.

Ale chwileczkę, jak mogło został pięć wolnych miejsc, skoro pokoje są trzyosobowe?

Popatrzmy raz jeszcze na rozwiązanie. Okazuje się, że wszystkie pokoje zostały zajęte, a dla pięciu kolonistów zabrakło miejsc. Zadanie to zawiera sprzeczne dane. Nie ma więc rozwiązania.

Polecenie 2

W prostokącie boki mają długości $6 cm$ i $8 cm$ . Przekątna ma długość $5 cm$ . Oblicz pole tego prostokąta.

R8kkPkpdYbpUK

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wydaje się, że pole tego prostokąta wynosi $48 {cm}^{2}$ . Jednak to stwierdzenie jest nieprawdziwe. Gdyż prostokąt o wymiarach podanych w treści zadania nie istnieje – przekątna nie może mieć mniejszą długość niż bok prostokąta. Zadanie zawiera sprzeczne dane.

Polecenie 3

Zbyszek ma $16$ książek przygodowych dwa razy więcej ma książek biograficznych, a pozostałe książki to powieści młodzieżowe. Ile książek młodzieżowych ma Zbyszek, jeśli wszystkich książek ma $40$ ?

R1TKiJ7qPzilK

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

$2 \cdot 16 = 32$ – tyle książek biograficznych ma Zbyszek

$40 - (16 + 32) = 40 - 48 = - 8$ – tyle książek młodzieżowych ma Zbyszek

Zadanie zawiera sprzeczne dane, bo liczba książek nie może wyrażać się liczbą ujemną. Zadanie nie ma rozwiązania.

Polecenie 4

Trzecia część uczniów pewnej klasy to chłopcy. Oblicz, ile jest dziewcząt w tej klasie, jeżeli wszystkich uczniów jest $25$ .

R1HzQrezopMZ0

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Oblicz $\frac{2}{3}$ liczby $25$ .

Skoro chłopcy to $\frac{1}{3}$ wszystkich uczniów, to liczba dziewcząt jest równa $\frac{2}{3}$ wszystkich uczniów.

$\frac{2}{3} \cdot 25 = \frac{50}{3} = 16 \frac{2}{3}$ .

Uzyskana liczba nie jest całkowita. Zadanie nie ma rozwiązania.

R1GtX49w7Efpj

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RX6xN23S1a45N

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RVMm2owtGO80E

Ćwiczenie 3

Przyporządkuj zadania do odpowiednich grup. Zadania, w których jest za mało danych. Możliwe odpowiedzi: 1. Antek na Dzień Kobiet przyniósł do klasy czekoladki i rozdał każdej z koleżanek. Ile czekoladek rozdał Antek?, 2. Uczniowie klasy

IVA

ustawili się na szkolnym dziedzińcu w

4

rzędach, po

6

osób w rzędzie. Uczniowie klasy

IVB

ustawili się w

2

rzędach, ale w każdym rzędzie było dwa razy tyle dzieci, co w rzędach utworzonych przez klasę

IVA

, czyli

12

uczniów. Ilu łącznie uczniów ustawiło się na dziedzińcu?, 3. Gertruda zamówiła

16

pączków. Dostarczono pączki w dwóch pudełkach. W pierwszym było

10

pączków, a w drugim

6

pączków. Cena jednego pączka wynosiła

3, 60 zł

. Jaka była wartość dostarczonych pączków?, 4. Matylda kupiła

2

znaczki po

2, 70 zł

za sztukę i

4

koperty. Ile zapłaciła?, 5. Henryk rozwiązuje codziennie

10

zadań z matematyki. A Janek

8

. Ile Zadań z matematyki rozwiąże Janek w ciągu tygodnia?, 6. Józek jedzie do babci rowerem z prędkością

12 \frac{km}{h}

. Z domu wyjechał o godzinie

8 : 15

. O której godzinie dotrze do babci?, 7. Basia wędrowała przez trzy dni. Pierwszego dnia przeszła

6 km

, a drugiego dnia o

2 km

więcej. Ile kilometrów przeszła trzeciego dnia? Zadania, w których jest za dużo danych. Możliwe odpowiedzi: 1. Antek na Dzień Kobiet przyniósł do klasy czekoladki i rozdał każdej z koleżanek. Ile czekoladek rozdał Antek?, 2. Uczniowie klasy

IVA

ustawili się na szkolnym dziedzińcu w

4

rzędach, po

6

osób w rzędzie. Uczniowie klasy

IVB

ustawili się w

2

rzędach, ale w każdym rzędzie było dwa razy tyle dzieci, co w rzędach utworzonych przez klasę

IVA

, czyli

12

uczniów. Ilu łącznie uczniów ustawiło się na dziedzińcu?, 3. Gertruda zamówiła

16

pączków. Dostarczono pączki w dwóch pudełkach. W pierwszym było

10

pączków, a w drugim

6

pączków. Cena jednego pączka wynosiła

3, 60 zł

. Jaka była wartość dostarczonych pączków?, 4. Matylda kupiła

2

znaczki po

2, 70 zł

za sztukę i

4

koperty. Ile zapłaciła?, 5. Henryk rozwiązuje codziennie

10

zadań z matematyki. A Janek

8

. Ile Zadań z matematyki rozwiąże Janek w ciągu tygodnia?, 6. Józek jedzie do babci rowerem z prędkością

12 \frac{km}{h}

. Z domu wyjechał o godzinie

8 : 15

. O której godzinie dotrze do babci?, 7. Basia wędrowała przez trzy dni. Pierwszego dnia przeszła

6 km

, a drugiego dnia o

2 km

więcej. Ile kilometrów przeszła trzeciego dnia?

IVA

ustawili się na szkolnym dziedzińcu w

4

rzędach, po

6

osób w rzędzie. Uczniowie klasy

IVB

ustawili się w

2

rzędach, ale w każdym rzędzie było dwa razy tyle dzieci, co w rzędach utworzonych przez klasę

IVA

, czyli

12

uczniów. Ilu łącznie uczniów ustawiło się na dziedzińcu?, 3. Gertruda zamówiła

16

pączków. Dostarczono pączki w dwóch pudełkach. W pierwszym było

10

pączków, a w drugim

6

pączków. Cena jednego pączka wynosiła

3, 60 zł

. Jaka była wartość dostarczonych pączków?, 4. Matylda kupiła

2

znaczki po

2, 70 zł

za sztukę i

4

koperty. Ile zapłaciła?, 5. Henryk rozwiązuje codziennie

10

zadań z matematyki. A Janek

8

. Ile Zadań z matematyki rozwiąże Janek w ciągu tygodnia?, 6. Józek jedzie do babci rowerem z prędkością

12 \frac{km}{h}

. Z domu wyjechał o godzinie

8 : 15

. O której godzinie dotrze do babci?, 7. Basia wędrowała przez trzy dni. Pierwszego dnia przeszła

6 km

, a drugiego dnia o

2 km

IVA

ustawili się na szkolnym dziedzińcu w

4

rzędach, po

6

osób w rzędzie. Uczniowie klasy

IVB

ustawili się w

2

rzędach, ale w każdym rzędzie było dwa razy tyle dzieci, co w rzędach utworzonych przez klasę

IVA

, czyli

12

uczniów. Ilu łącznie uczniów ustawiło się na dziedzińcu?, 3. Gertruda zamówiła

16

pączków. Dostarczono pączki w dwóch pudełkach. W pierwszym było

10

pączków, a w drugim

6

pączków. Cena jednego pączka wynosiła

3, 60 zł

. Jaka była wartość dostarczonych pączków?, 4. Matylda kupiła

2

znaczki po

2, 70 zł

za sztukę i

4

koperty. Ile zapłaciła?, 5. Henryk rozwiązuje codziennie

10

zadań z matematyki. A Janek

8

. Ile Zadań z matematyki rozwiąże Janek w ciągu tygodnia?, 6. Józek jedzie do babci rowerem z prędkością

12 \frac{km}{h}

. Z domu wyjechał o godzinie

8 : 15

. O której godzinie dotrze do babci?, 7. Basia wędrowała przez trzy dni. Pierwszego dnia przeszła

6 km

, a drugiego dnia o

2 km

więcej. Ile kilometrów przeszła trzeciego dnia?

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RZvwecw1aOOrd

Ćwiczenie 4

Łączenie par. Zaznacz, które stwierdzenie jest prawdziwe, a które fałszywe.. Zadanie - Piotrek ma psy i koty - razem $10$ zwierząt. Kotów ma $7$ , a psów o $4$ więcej. Ile psów ma Piotrek? - nie ma rozwiązania.. Możliwe odpowiedzi: Prawda, Fałsz. Zadanie - Pole powierzchni ściany bocznej sześcianu jest równe $36$ , a krawędź podstawy ma długość Zadanie - Pole powierzchni ściany bocznej sześcianu jest równe $6$ . Oblicz objętość tego sześcianu. - zawiera nadmiar danych.. Możliwe odpowiedzi: Prawda, Fałsz. Zadanie - Czekolada kosztuje $4 zł$ . Ile takich czekolad możemy kupić za $13 zł?$ - nie ma rozwiązania.. Możliwe odpowiedzi: Prawda, Fałsz. Zadanie - Ania jest starsza od Mani o $9$ lat. O ile lat młodsza była Mania od Ani $3$ lata temu? - ma dwa rozwiązania.. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 5

RtKnGszRB2yvI

Oceń, czy zadanie zostało dobrze rozwiązane. Jeśli dobrze - przeciągnij TAK, jeśli źle przeciągnij NIE.

Za $3$ pączki i rurkę z kremem zapłacono $15, 20 zł$ . Za pączka i rurkę z kremem zapłacono $7, 20 zł$ . Ile kosztuje rurka z kremem?
Rozwiązanie
Za $2$ rurki z kremem zapłacono $15, 20 zł - 7, 20 zł = 8 zł$ .
Jedna rurka z kremem kosztuje więc: $8 zł : 2 = 4 zł$ .
1. TAK, 2. TAK, 3. NIE, 4. NIE
Jurek na przebycie drogi z domu do szkoły potrzebuje $10$ minut, a jego młodsza siostra Beata potrzebuje $20$ minut. We wtorek Jurek wyruszył do szkoły, a Beata równocześnie wyruszyła ze szkoły do domu. Po ilu minutach spotkają się?
Rozwiązanie
Oznaczmy przez $t$ czas, po jakim spotka się rodzeństwo.
Ponieważ rodzeństwo spotka się po drodze, więc zachodzi równość $10 t = 20 t$ .
$10 t = 20 t : t$
$10 = 20$
Otrzymaliśmy sprzeczność, zatem zadanie nie ma rozwiązania.
1. TAK, 2. TAK, 3. NIE, 4. NIE

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Za $2$ pączki zapłacono $8 zł$ , a nie za dwie rurki z kremem.
Długość przebytej drogi obliczamy, mnożąc prędkość, z jaką porusza się dana osoba przez czas ruchu.

RWkHFNvb7vcPQ

Ćwiczenie 6

Połącz w pary zadanie i uzasadnienie, że zadanie nie ma rozwiązania. Iloczyn cyfr liczby dwucyfrowej jest równy

17

. Znajdź tę liczbę, jeżeli jej cyfra jedności wynosi

4

. Możliwe odpowiedzi: 1. Największa różnica cyfr liczby dwucyfrowej to

9

., 2. Cyfra danej liczby nie może wyrażać się ułamkiem., 3. Suma cyfr liczby dwucyfrowej nie może być większa od

18

., 4. Cyfrą dziesiątek liczby dwucyfrowej nie może być zero. Suma cyfr liczby dwucyfrowej jest równa

21

. Znajdź tę liczbę. Możliwe odpowiedzi: 1. Największa różnica cyfr liczby dwucyfrowej to

9

., 2. Cyfra danej liczby nie może wyrażać się ułamkiem., 3. Suma cyfr liczby dwucyfrowej nie może być większa od

18

., 4. Cyfrą dziesiątek liczby dwucyfrowej nie może być zero. Różnica cyfr liczby dwucyfrowej jest równa

11

. Znajdź tę liczbę. Możliwe odpowiedzi: 1. Największa różnica cyfr liczby dwucyfrowej to

9

., 2. Cyfra danej liczby nie może wyrażać się ułamkiem., 3. Suma cyfr liczby dwucyfrowej nie może być większa od

18

., 4. Cyfrą dziesiątek liczby dwucyfrowej nie może być zero. Różnica liczby dwucyfrowej podzielnej przez

20

i liczby dwucyfrowej, którą otrzymamy w wyniku przestawienia cyfr tej liczby jest równa

36

. Znajdź tę liczbę. Możliwe odpowiedzi: 1. Największa różnica cyfr liczby dwucyfrowej to

9

., 2. Cyfra danej liczby nie może wyrażać się ułamkiem., 3. Suma cyfr liczby dwucyfrowej nie może być większa od

18

., 4. Cyfrą dziesiątek liczby dwucyfrowej nie może być zero.

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

Jaś miał do pokonania $1230 km$ . Pierwszego dnia przejechał $639 km$ , drugiego dnia przejechał o $12 km$ więcej. Ile kilometrów przejechał Jaś trzeciego dnia?

R18ucR8EjHhq7

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Jaś drugiego dnia przejechał $639 + 12 = 651$ kilometrów.

1230 - (639 + 639 + 12) = 1230 - 1290 = - 60

Liczba kilometrów nie może wyrażać się liczbą ujemną – zadanie nie ma rozwiązania.

Ćwiczenie 8

Suma cyfr pewnej liczby dwucyfrowej $A$ jest mniejsza od $8$ . Jeśli przestawimy cyfry w tej liczbie – otrzymamy liczbę dwucyfrową większą od liczby $A$ . Znajdź liczbę $A$ .

R1IShoDJ4cUZh

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Liczby dwucyfrowe, których suma cyfr jest mniejsza od $8$ : $10$ , $11$ , $12$ , $13$ , $14$ , $15$ , $16$ , $20$ , $21$ , $22$ , $23$ , $24$ , $25$ , $30$ , $31$ , $32$ , $33$ , $34$ , $40$ , $41$ , $42$ , $43$ , $50$ , $51$ , $52$ , $60$ , $61$ , $70$ .

Liczba $A$ i liczba o przestawionych cyfrach to liczby dwucyfrowe. Zatem cyfrą jedności liczby $A$ nie może być zero. Aby liczba o przestawionych cyfrach była większa od liczby $A$ , cyfra jedności liczby $A$ musi być większa od cyfry dziesiątek.

Liczba $A$ może więc być równa: $12$ , $13$ , $14$ , $15$ , $16$ , $23$ , $24$ , $25$ lub $34$ .

Słownik

zadanie tekstowe

opis słowny związków między pewnymi wielkościami, zawierający pytanie lub polecenie.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

2. Rozwiązywanie zadań tekstowych z wykorzystaniem ułamków zwykłych

4. Zapisywanie treści prostych zadań za pomocą równań