Korzystając z rysunku, ułożymy zadanie matematyczne.

R17TxXEWy2KLP

Grafika przedstawiająca cztery czerwone jabłka, dwie żółte gruszki oraz siedem fioletowych śliwek.

$\text{I}$ sposób

Odnosimy się bezpośrednio do ilustracji i zadajemy pytania, na które można odpowiedzieć, wykonując obliczenia w pamięci.

Na stole leżą jabłka, gruszki i śliwki. O ile więcej jest śliwek niż jabłek? Ile razy więcej jest jabłek niż gruszek? Których owoców jest więcej – gruszek czy śliwek? Ile wszystkich owoców leży na stole?

$\text{II}$ sposób

Teraz warstwę werbalną wzbogacamy, dodając opisy czynności, które zostały wykonane. Znalezienie odpowiedzi do utworzonego zadania, będzie wymagało wykonania kilku obliczeń. Jednak w dalszym ciągu niektóre dane trzeba będzie odczytać z rysunku.

Na stole leżały jabłka, gruszki i śliwki (patrz rysunek). Maciek zjadł dwie śliwki, Mariusz zjadł dwa jabłka, a Mariola położyła na stole jeszcze pięć gruszek. Ile teraz wszystkich owoców leży na stole? Jaką część wszystkich owoców stanowią gruszki?

$\text{III}$ sposób

W tym przypadku wymyślona przez nas treść, tylko luźno związana jest z ilustracją, która pełni rolę „ozdobnika” do zadania. Co prawda, spoglądając na ilustrację, można przewidzieć, jakie liczby powinniśmy otrzymać, ale dla sprawdzającego rozwiązanie, ważna będzie zastosowana metoda postępowania, nie tylko odpowiedź.

Na stole leżą jabłka, gruszki i śliwki – razem $13$ sztuk. Jabłek jest dwa razy więcej niż gruszek. Śliwek jest o $3$ więcej niż jabłek. Ile gruszek leży na stole?

Rozwiązanie:
$x$ – liczba gruszek
$2x$ – liczba jabłek
$2x+3$ – liczba śliwek
$x+2x+\left(2x+3\right)$ – liczba wszystkich owoców

Odpowiedź:
Na stole leżą dwie gruszki.

Ułożymy zadanie matematyczne, korzystając z poniższej tabelki.

Domyślamy się, że tabelka zawiera liczby zdobytych punktów przez trzech zawodników w rozgrywkach trzyetapowych. Punkty zapisane są za pomocą liczb dodatnich, ujemnych oraz zera. Rozwiązanie układanego przez nas zadanie będzie wymagało znajomości wykonywania działań na liczbach całkowitych.

$\text{I}$ sposób

W tabelce zapisano liczby punktów zdobyte przez poszczególnych zawodników w klasowym konkursie matematycznym.
Ile łącznie punktów zdobył Wiesiek?
Ile punktów łącznie zdobyli zawodnicy w $\text{I}$ rundzie konkursu?
Który zawodnik zdobył najwięcej punktów w $\text{II}$ rundzie?
Jaka jest średnia arytmetyczna liczby punktów zdobytych przez zawodników w $\text{III}$ rundzie konkursu?
Który zawodnik zwyciężył?

$\text{II}$ sposób

Teraz propozycja trudniejszego zadania, wymagającego starannego przeanalizowania treści.

W tabelce zapisano liczby punktów zdobyte przez poszczególnych zawodników w eliminacjach do finału szkolnego konkursu matematycznego. Aby zakwalifikować się do dalszych eliminacji, łączna suma zdobytych punktów musi wynosić co najmniej trzy i różnica między najwyższym wynikiem zawodnika w rundzie a najniższym wynikiem zawodnika w rundzie nie może być większa niż $3$.
Który z chłopców zakwalifikował się do finału konkursu?

Rozwiązanie:
Obliczamy, ile punktów łącznie zdobył każdy z chłopców.
Wiesiek: $-1+5+2=6⩾3$.
Romek: $2+0+1=3⩾3$.
Damian: $-1-3+6=2<3$.
Co najmniej trzy punkty zdobyli Wiesiek i Romek. Sprawdzamy teraz czy dla obu chłopców różnica między najwyższym, a najniższym wynikiem jest nie większa niż trzy.
Wiesiek: $5-\left(-1\right)=6>3$.
Romek: $2-0=2<3$.

Odpowiedź:
Do finału konkursu zakwalifikował się Romek.

R2krEzsyC08gj

Ilustracja przedstawiająca gitarę w kolorze brązowym. Po prawej stronie fotografii znajduje się czarny napis na szarym tle: "Obniżka ceny o 25% lub o 55 zł". Poniżej, na różowym tle zapisano cenę instrumentu 240 zł.

Tym razem w obu ułożonych przez nas zadaniach będzie to samo pytanie. Ale w $\text{I}$ sposobie dodamy jeszcze pytania pomocnicze, które ukierunkują rozwiązującego na znalezienie rozwiązania.
Natomiast w $\text{II}$ sposobie, rozwiązujący będzie samodzielnie musiał ustalić sposób postępowania.

$\text{I}$ sposób

Gitara kosztowała $240 \mathrm{zł}$. Teraz można ją kupić z $25\%$ zniżką lub ze zniżką wynoszącą $55 \mathrm{zł}$.
Ile kosztuje gitara po obniżce ceny o $25\%$?
Ile kosztuje gitara po obniżce ceny o $55 \mathrm{zł}$?
Która opcja jest korzystniejsza dla kupującego – obniżka ceny gitary o $25\%$ czy obniżka o $55 \mathrm{zł}$?

$\text{II}$ sposób

Gitara kosztowała $240 \mathrm{zł}$. Teraz można ją kupić z $25\%$ zniżką lub ze zniżką wynoszącą $55 \mathrm{zł}$.
Która opcja jest korzystniejsza dla kupującego – obniżka ceny gitary o $25\%$ czy obniżka o $55 \mathrm{zł}$?

Rozwiązanie:
$25\%$ liczby $240$ to $\frac{1}{4}$ tej liczby, czyli $240:4=60$.

Gitara po obniżce o $25\%$ kosztuje $180 \mathrm{zł}$.

Gitara po obniżce o $55 \mathrm{zł}$ kosztuje $185 \mathrm{zł}$.

Odpowiedź:
Dla kupującego korzystniejsza jest obniżka ceny gitary o $25\%$.

Rvk232r4gzgfe

Grafika przedstawiająca trzy różne drogi od punktu oznaczonego gwiazdką do punktu oznaczonego trójkątem. Ścieżki ukazane są na tle wykonanym z siateczki kwadratów. Droga "A" oznaczona jest kolorem niebieskim i wygląda następująco: dwa kroki w dół, trzy w prawo, dwa w dół, jeden w prawo, jeden w dół, jeden w prawo, jeden w dół, sześć w prawo i dwa w dół. Droga "B" oznaczona jest kolorem pomarańczowym i wygląda następująco: dwa kroki w prawo, jeden w dół, trzy w prawo, jeden w dół, sześć w prawo i sześć w dół. Droga "C" oznaczona jest kolorem zielonym i wygląda następująco: siedem kroków w dół, dziesięć w prawo, jeden w dół, jeden w prawo.

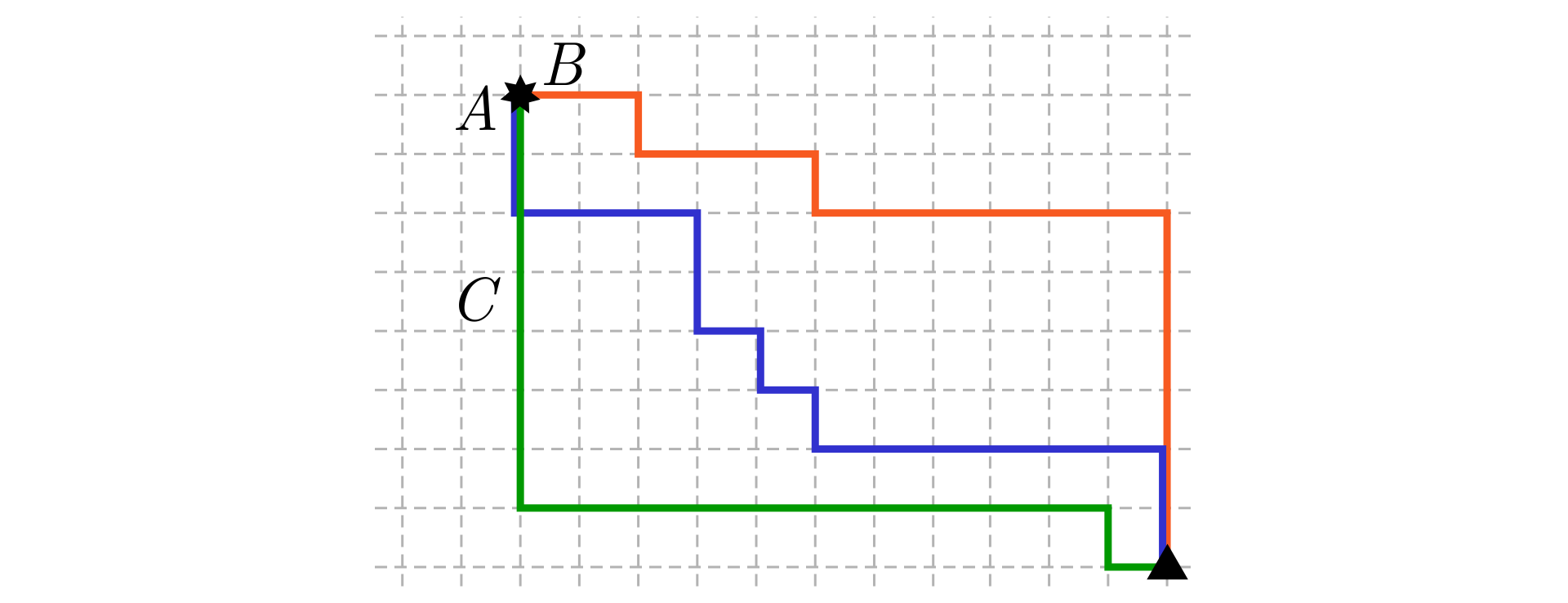
Mamy ułożyć zadanie na podstawie rysunku. Może to być zadanie czysto geometryczne lub obudowane w pewną historyjkę.

Sposób $\text{I}$

Z punktu oznaczonego gwiazdką do punktu oznaczonego trójkątem prowadzą po liniach sieci trzy drogi A, B, C. Która z tych dróg jest najkrótsza?

Sposób $\text{II}$

Z zamku oznaczonego na rysunku gwiazdką, wyruszają równocześnie trzej rycerze: A, B, C. Rycerze podążają do wieży, oznaczonej na rysunku trójkątem, gdzie okrutna wiedźma więzi królewnę Edytę. Rycerze mogą poruszać się tylko po wyznaczonych trasach, biegnących po liniach sieci. Inaczej wiedźma zamieni ich w kamienie. Rycerz A po trasie niebieskiej, rycerz B po trasie czerwonej, rycerz C po trasie zielonej.

Który z rycerzy pierwszy dotrze do celu, jeśli rycerze poruszają się z tą samą prędkością?

Rozwiązanie:
Długość trasy rycerza A: $19$.
Długość trasy rycerza B: $19$.
Długość trasy rycerza C: $19$.

Odpowiedź:
Rycerze mają do przebycia trasy tej samej długości, a więc dotrą równocześnie do celu.
Zauważmy przy tym, że każda trasa prowadząca z punktu „gwiazdka” w prawo i w dół do punktu „trójkąt” będzie miała długość również równą $19$. Jak myślisz, dlaczego?

Ułożymy zadanie, wykorzystując poniższe równości.

RngI0dcxaoEy8

Na grafice ukazane są trzy równania na różowym tle. Pierwsze: $\frac{a+b}{2}=3$. Drugie: $\frac{b+c}{2}=5$. Trzecie: $\frac{a+c}{2}=4$.

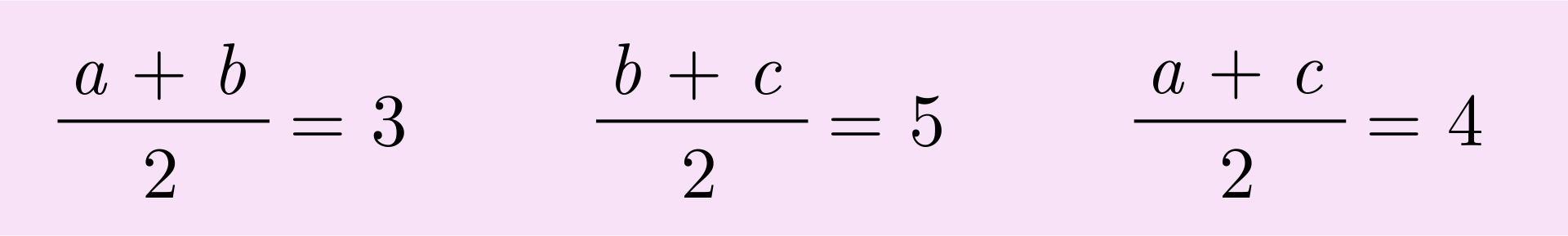
Sposób $\text{I}$

Zadanie algebraiczne
Dane są liczby $a$, $b$, $c$. Średnia arytmetyczna liczb $a$ i $b$ jest równa $3$. Średnia arytmetyczna liczb $b$ i $c$ jest równa $5$. Średnia arytmetyczna liczb $a$ i $c$ jest równa $4$. Znajdź średnią arytmetyczną liczb $a$, $b$, $c$.

Rozwiązanie:
Przekształcamy każdą z zapisanych równości tak, aby otrzymać sumy liczb.

Zapisujemy otrzymane sumy jedna pod drugą.

Następnie dodajemy je stronami.

Aby obliczyć średnią arytmetyczną liczb $a$, $b$, $c$ wystarczy podzielić obie strony otrzymanej równość przez $3$.

Odpowiedź:
Średnia arytmetyczna liczb $a$, $b$, $c$ jest równa $4$.

Sposób $\text{II}$

Zapiszemy teraz zadanie, którego treść będzie prawie identyczna jak w sposobie $\text{I}$, jednak przez większość uczniów na pewno zostanie uznane za znaczenie trudniejsze, ze względu na nielubiane sformułowanie $\dots$ wykaż, że $\dots$.

Dane są liczby $a$, $b$, $c$. Średnia arytmetyczna liczb $a$ i $b$ jest równa $3$. Średnia arytmetyczna liczb $b$ i $c$ jest równa $5$. Średnia arytmetyczna liczb $a$ i $c$ jest równa $4$. Wykaż, że średnia arytmetyczna liczb $a$, $b$, $c$ jest równa $4$.

Rozwiązanie tego zadania przebiega tak samo jak w Sposobie $\text{I}$.

opis sytuacji zadania tekstowego, w której osadzone są poszukiwane wielkości.

dane i niewiadome zadania tekstowego powiązane zależnościami, tworzące rzeczywisty problem matematyczny, który należy rozwiązać.