Zadania tekstowe
7. Łamigłówki
Zagadki, łamigłówki, rebusy to zadania, których rozwiązań należy poszukiwać na podstawie logicznego wnioskowania, wiedzy lub abstrakcyjnego myślenia.
Zagadki towarzyszą ludzkości od zarania dziejów. Spotkamy je w mitologii, tekstach średniowiecznych filozofów i współcześnie – na wielu stronach internetowych. Łamigłówki rozwijają wyobraźnię, kreatywność, spostrzegawczość, uczą interdyscyplinarnego postrzegania rzeczywistości.
Zagadki mogą mieć jedno rozwiązanie, kilka rozwiązań, a nawet mogą nie mieć rozwiązania.
Dla wprawy, spróbuj przeanalizować jedną z najbardziej znanych zagadek, której różne wersje krążą od stuleci w literaturze matematycznej. Co prawda większość osób uzasadnia poprawność swojej odpowiedzi na gruncie matematyki wyższej, ale może Tobie uda się znaleźć prostsze rozwiązanie.
Zagadka mrówki

Po elastycznej gałęzi, której początkowa długość wynosi metrów idzie mrówka z prędkością centymetr na sekundę. Gałąź rozciąga się z prędkością centymetrów na sekundę. Mrówka startuje z prawego, nieruchomego końca gałęzi. Czy mrówka w skończonym czasie dojdzie do lewego jej końca?
W tym materiale pokażemy przykłady różnych zagadek, które może zainspirują Cię do układania własnych łamigłówek i prezentowania ich znajomym.
Pierwszy typ łamigłówek, którym się zajmiemy, to znane Ci na pewno łamigłówki z zapałkami. Najczęściej za ich pomocą układane są równości arytmetyczne. Należy przełożyć jedną lub dwie zapałki tak, aby otrzymana równość była prawdziwa. Do rozwiązania takiej zagadki potrzebna jest zwykła znajomość rzymskiego sposobu zapisu liczb.
Układamy takie łamigłówki zapałczane, aby trzeba było przełożyć tylko jedną zapałkę, chcąc otrzymać równość prawdziwą.
Najprościej jest, gdy trzeba tylko zmienić znaki działań (pierwsza równość) lub liczbę z mniejszej zmienić na większą (druga równość).
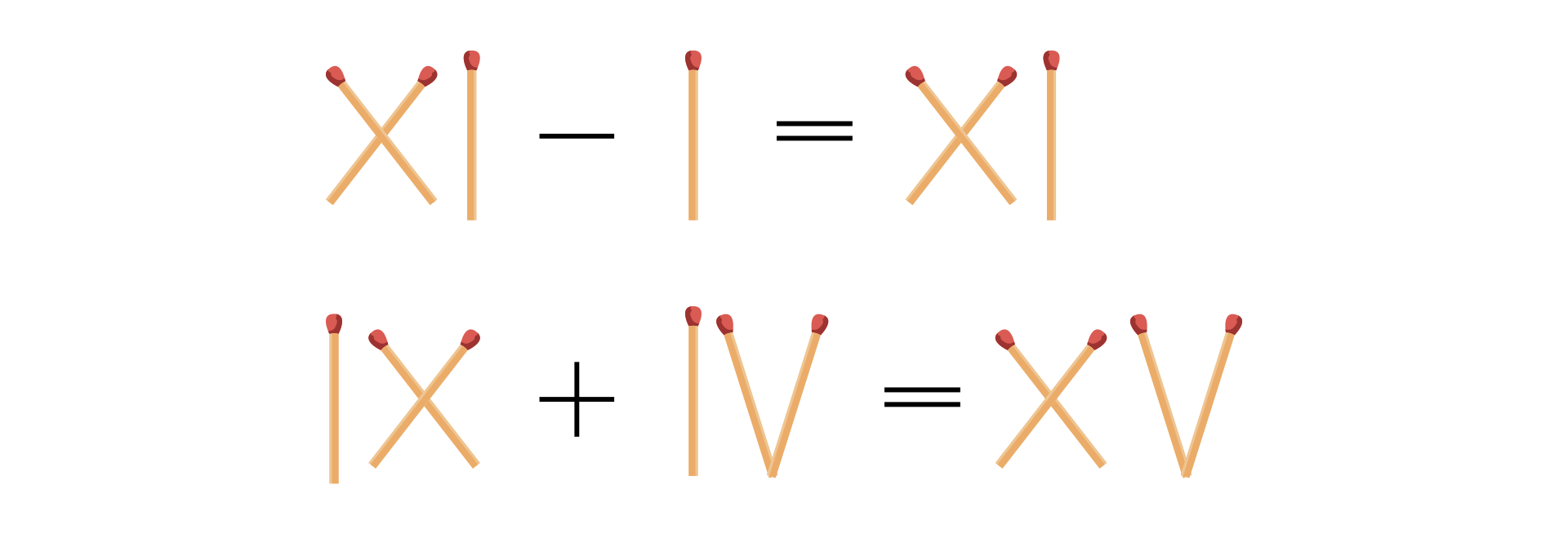
Symbol oznacza w zapisie rzymskim liczbę , a symbol to pięć.
W pierwszym przypadku wystarczy odejmowanie zamienić na dodawanie, a w drugim liczbę zamienić na .
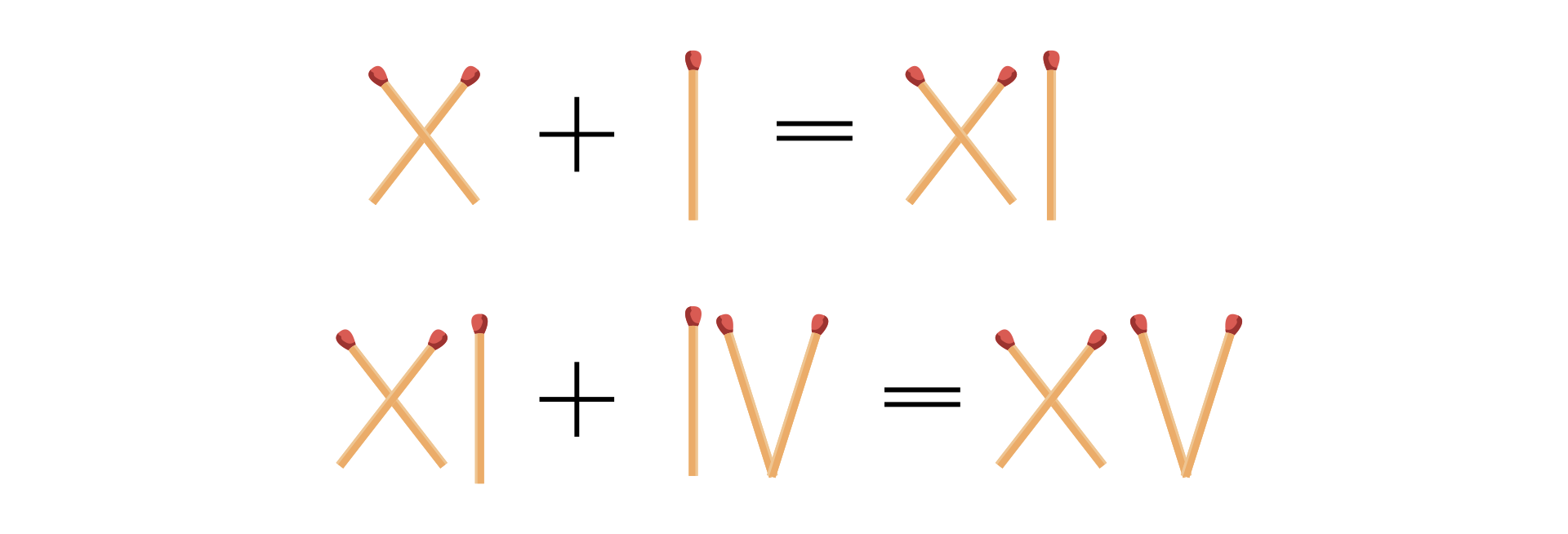
Ułóż w podobny sposób kilka własnych zagadek zapałczanych.
Następny popularny typ układanek liczbowych to kwadraty magiczne.
Kwadrat magiczny to kwadratowa tablica, w pola której wpisano liczby w ten sposób, że ich suma w każdym wierszu, w każdej kolumnie i na każdej przekątnej jest taka sama. Najczęściej wymaga się, aby liczby w kwadracie magicznym nie powtarzały się i były liczbami naturalnymi.
Utworzymy własny kwadrat magicznykwadrat magiczny. Ustalamy sumę magiczną – niech to będzie .
Na przekątnej wpisujemy takie liczby, aby ich suma była równa .
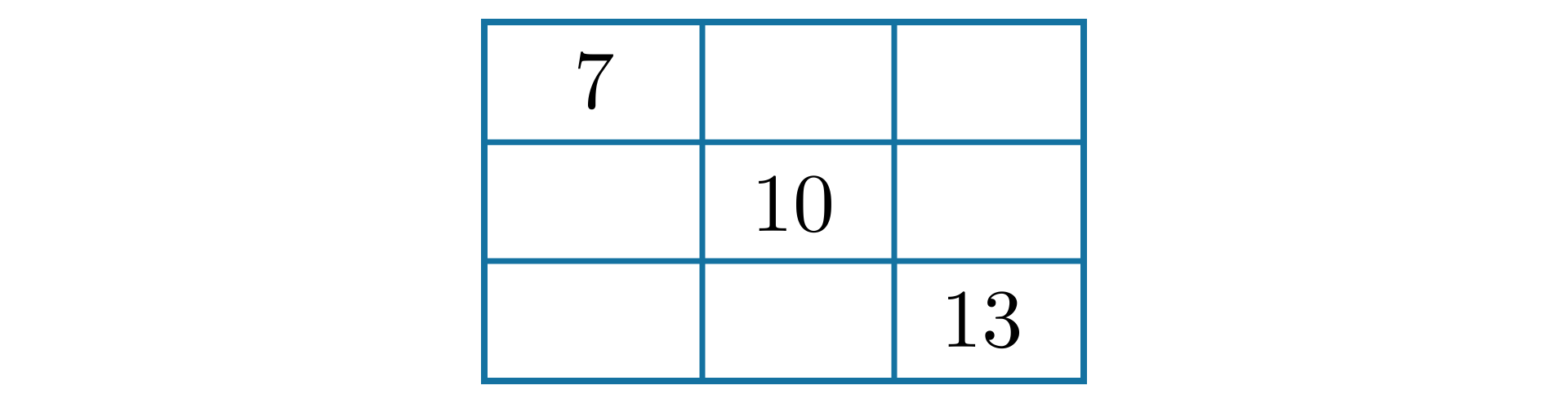
Na drugiej przekątnej dopisujemy takie liczby, aby ich suma też była równa .
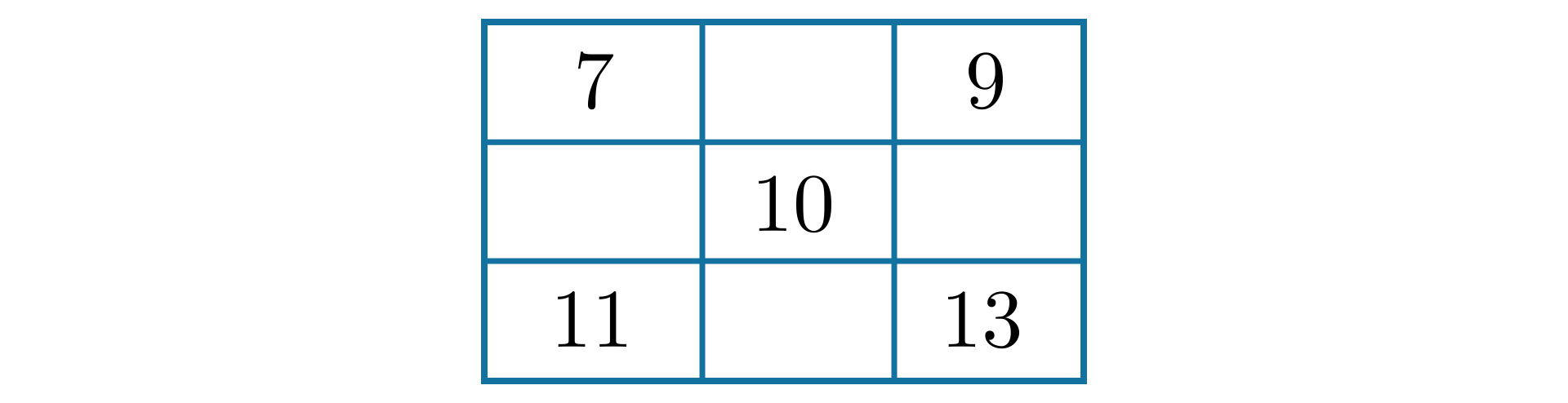
Uzupełniamy wolne pola.
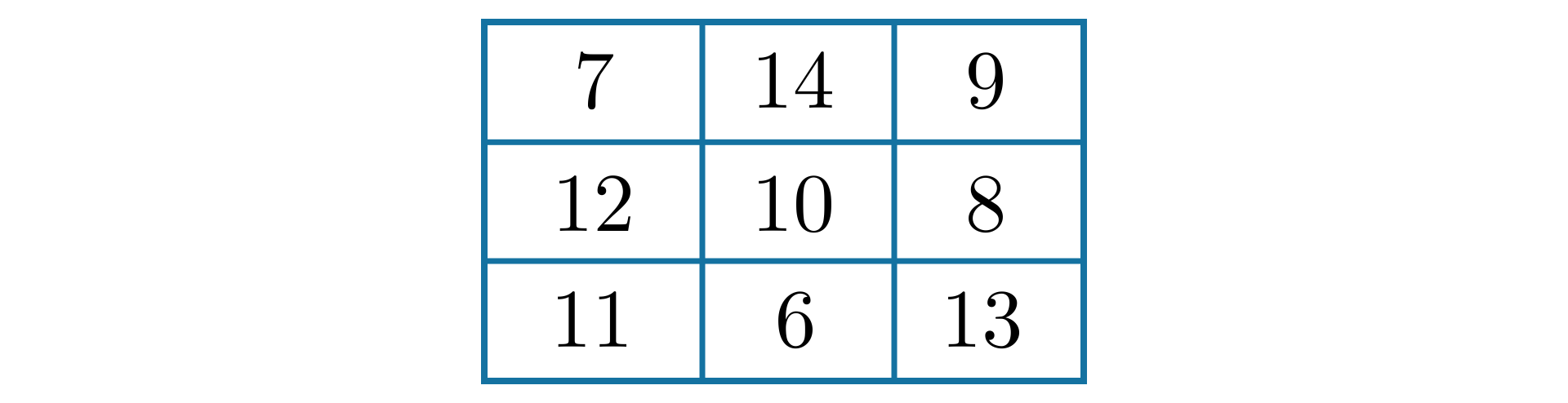
Jeśli chcesz stworzyć własny kwadrat magicznykwadrat magiczny, możesz postąpić w podobny sposób. Możesz też wykorzystać kwadrat z Przykładu , na przykład dodając do każdej liczby w kwadracie tę samą liczbę. Otrzymasz w ten sposób inny kwadrat magiczny.
Zagadki liczbowe często wymagają nie tylko sprawnych obliczeń, ale również logicznego myślenia.
Zbudujemy rebus liczbowy zakładając, że tym samym „symbolom” odpowiadają te same cyfry.
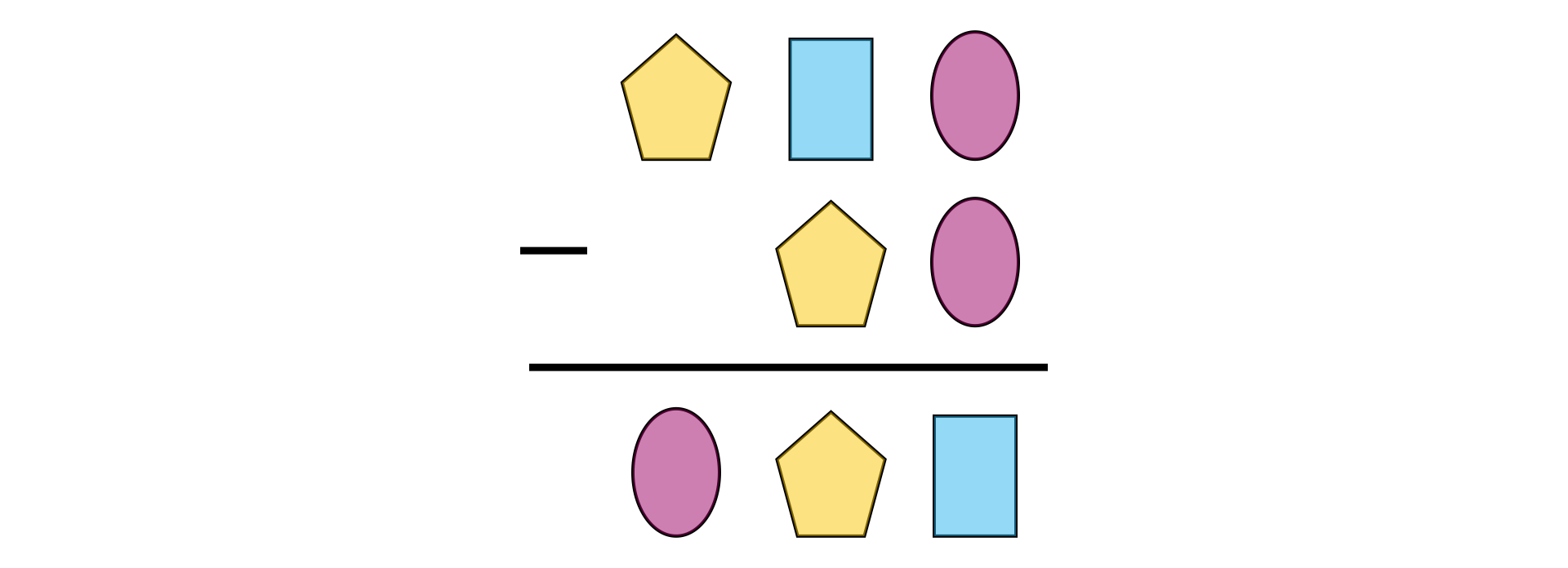
Układaliśmy rebus „od tyłu”. Jeśli bowiem odejmiemy dwie liczby, których cyfry jedności są takie same, to w wyniku otrzymamy liczbę, której cyfrą jedności jest zero.
Np.
Zatem cyfra odpowiadająca prostokątowi to .
Teraz od odejmujemy pewną liczbę i w wyniku otrzymujemy tę samą liczbę. Jest tylko jedna możliwość – ta liczba to .
Zatem żółtemu pięciokątowi odpowiada cyfra . I jest już oczywiste, że różowej figurze odpowiada .
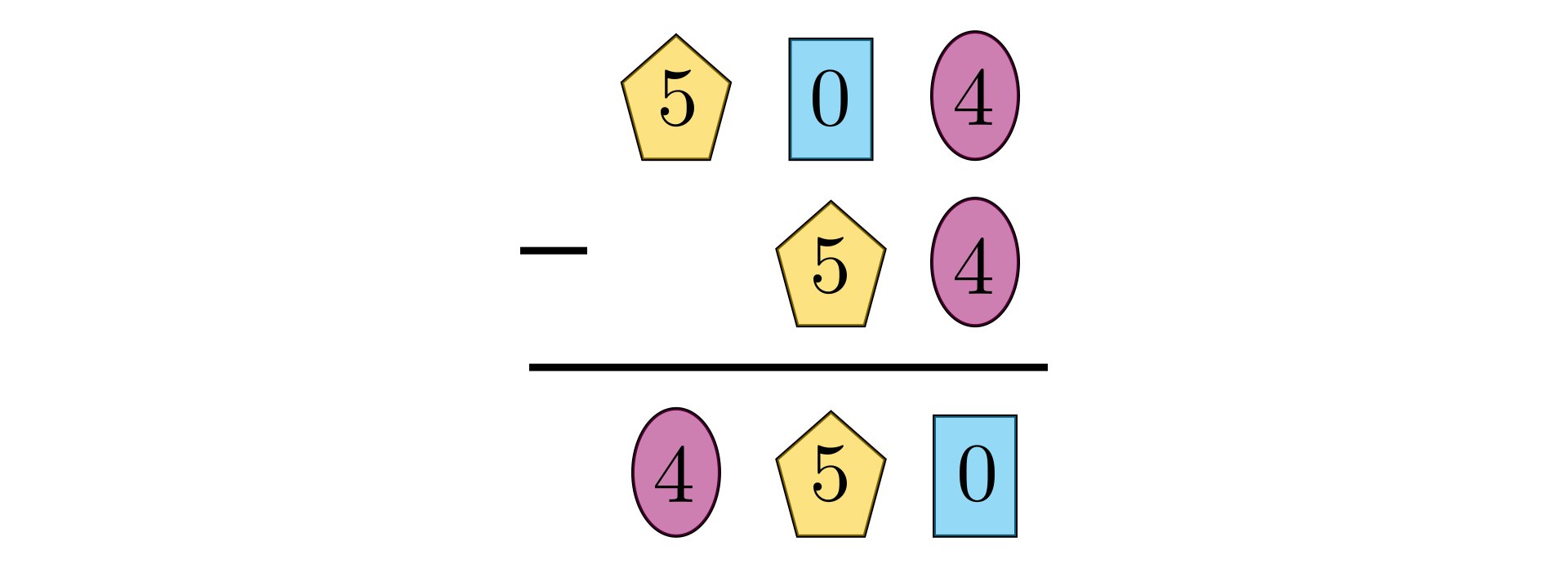
Wzorując się na podanym przykładzie, stwórz własną zagadkę liczbową.
Trudne zadania matematyczne warto czasem zapisać w formie wiersza lub krótkiego opowiadania. Stanie się ono wtedy na tyle zagadkowe, że z przyjemnością je rozwiążemy
Matematyczna zagadka inspirowana wierszem J. Tuwima Idzie Grześ.

Idzie Grześ przez wieś, worek piasku niesie. A przez dziurkę piasek ciurkiem sypie się za Grzesiem.
Już kilogramów piasku się wysypało,
A Grześ idzie, jakby się nic nie stało.
Z każdą minutą piasku ubywa.
Grześ pogwizduje i czas mu mile upływa.
Po ośmiu minutach zawartość worka o połowę się zmniejszyła,
A dziura w worku tak się powiększyła,
Że gdy Grześ do domu wrócił,
Z grzbietu pusty worek zrzucił.
Odpowiedz, jeśli łaska
Ile początkowo w worku było piasku.
Wierszyk nie jest ściśle doprecyzowany. Jego celem jest sprowokowanie dyskusji – czy, po wspomnianych w wierszu ośmiu minutach, zawartość worka zmniejszyła się o połowę początkowej zawartości, czy o połowę zawartości worka, z którego już wysypało się piasku.
W zależności od tego, jakie ustalenia przyjmiemy, otrzymamy, że początkowo w worku było piasku lub .
Ciekawe problemy można znaleźć, sięgając do historii matematyki. Jedną z takich zagadek zamieścił w swoim dziele Liber abaci włoski, trzynastowieczny matematyk Leonardo z Pizy, zwany Fibonaccim.
Zagadka Fibonacciego
Kupiec podczas swojej podróży handlowej do Wenecji podwoił tam swój początkowy kapitał, a następnie wydał denarów. Potem udał się do Florencji, gdzie znowu podwoił liczbę posiadanych denarów i wydał . Po powrocie do Pizy po raz kolejny podwoił swój majątek, wydał dwanaście denarów i został bez grosza. Ile denarów miał na początku?
Rozwiązanie tej zagadki nie nastręcza kłopotów, jeśli narysujemy odpowiedni graf, opisujący treść zadania.
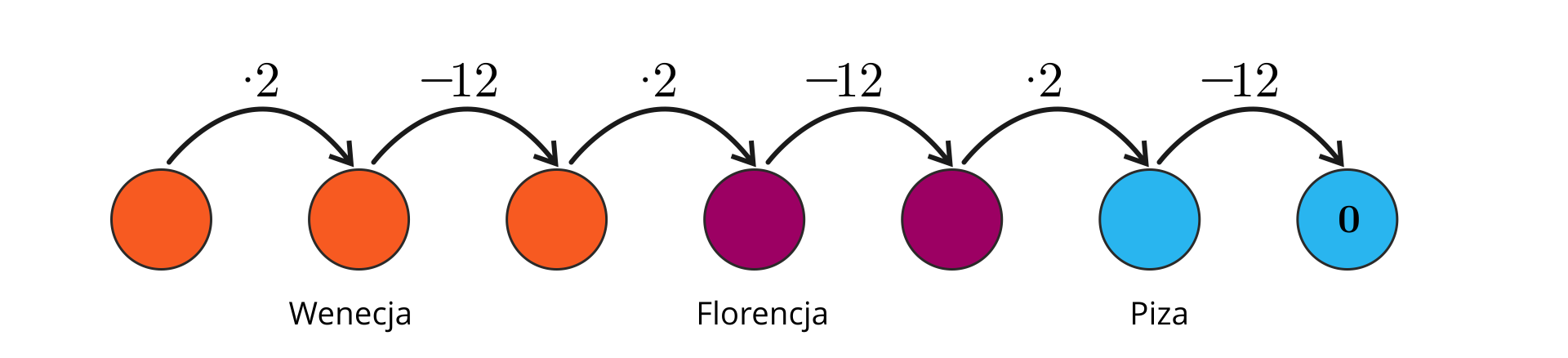
Uzupełniamy rysunek, wykonując działania odwrotne.
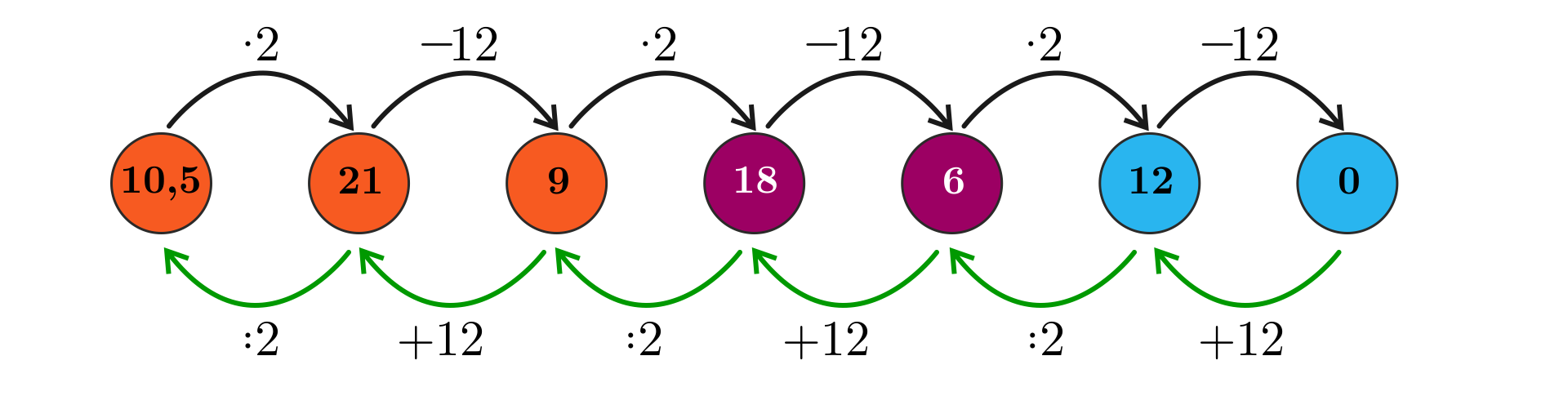
Z grafu odczytujemy, że kupiec miał początkowo denara.
Spróbuj zadanie to rozwiązać innym sposobem.
Wśród rozrywek matematycznych ważną rolę pełnią zadania logiczne. Możemy je rozwiązywać graficznie lub sporządzając odpowiednią tabelkę.
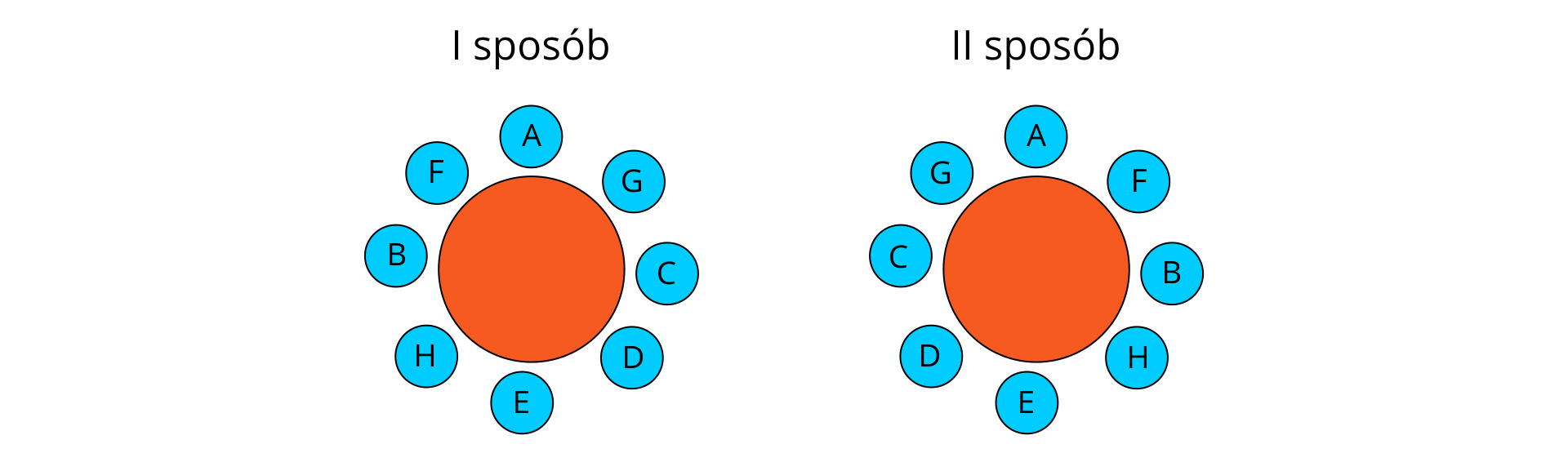
Panowie A, B, C, D, E, F, G, H mają zasiąść wspólnie przy okrągłym stole. Nie jest to jednak takie łatwe, bo:
pan F nie lubi pana C, ale lubi pana B,
pan D nie lubi pana G, ale bardzo lubi pana E,
pan A przyjaźni się z panem G i F i chce siedzieć obok nich,
pan H koniecznie chce siedzieć obok panów B i E.
Jak powinni usiąść panowie?
Panowie | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
A | ||||||||
B | ||||||||
C | ||||||||
D | ||||||||
E | ||||||||
F | ||||||||
G | ||||||||
H |
Panowie | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
A | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | ||
B | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | ||
C | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | |
D | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | ||
E | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | ||
F | brak treści | brak treści | brak treści | brak treści | brak treści | |||
G | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści | ||
H | brak treści | brak treści | brak treści | brak treści | brak treści | brak treści |
Zaczynamy od pana A – powinien siedzieć między panami F i G. Obok pana F zasiądzie pan B.
Teraz usadzamy pana H, między panami B i E.
Obok pana E usiądzie pan D.
Wybieramy miejsce dla pana C – nie może siedzieć obok pana F, zatem pozostaje tylko jedna możliwość – usiądzie między panami G i D.
Jako podsumowanie naszych rozważań o łamigłówkach – rozwiąż rebus.
Rozwiąż rebus

Prezentacja multimedialna
Zapoznaj się z prezentacją. Spróbuj rozwiązać każdą z podanych tam zagadek swoim sposobem, a dopiero następnie porównaj z podanym rozwiązaniem.
Slajd pierwszy:
Lektor mówi: Łamigłówki, zagadki, rebusy matematyczne to rozrywki umysłowe pobudzające wyobraźnię, kreatywność. Wymagają szerszego spojrzenia na rozwiązywany problem, zastosowania nietypowych pomysłów. Łamigłówki mogą być różne – arytmetyczne, algebraiczne, geometryczne, logiczne. W prezentacji podamy kilka przykładów zagadek matematycznych, zachęcamy cię do samodzielnego układania zadań podobnego typu. Na początek kilka zagadek wymagających tylko logicznego myślenia.
Na slajdzie prezentowany jest film składający się z kadrów na których dzieci bawią się zabawkami logicznymi. Są to drewniane łamigłówki, kostki Rubika w kształcie ostrosłupa, puzzle.
Slajd drugi:
Lektor mówi: Zagadka pierwsza. Łatwa. Jej rozwiązanie wymaga uważnego przeanalizowania rozmowy dwóch pań. Czy masz zwierzęta domowe – zapytała pani Jola panią Ewę. Ależ oczywiście. Mam nawet więcej niż dwa zwierzęta. – odpowiedziała pani Ewa. Wszystkie, oprócz dwóch są psami. Wszystkie, z wyjątkiem dwóch to koty. Wszystkie, z wyjątkiem dwóch to świnki. Ile zwierząt domowych ma pani Ewa?
Prawda, że łatwa zagadka? Oczywiście – pani Ewa ma trzy zwierzątka domowe: psa, kota i świnkę.
W centralnym miejscu na slajdzie prezentowane jest zdjęcie dwóch kobiet siedzących na kocu. Po lewej stronie znajduje się również zdjęcie kota, a po prawej psa.
Slajd trzeci:
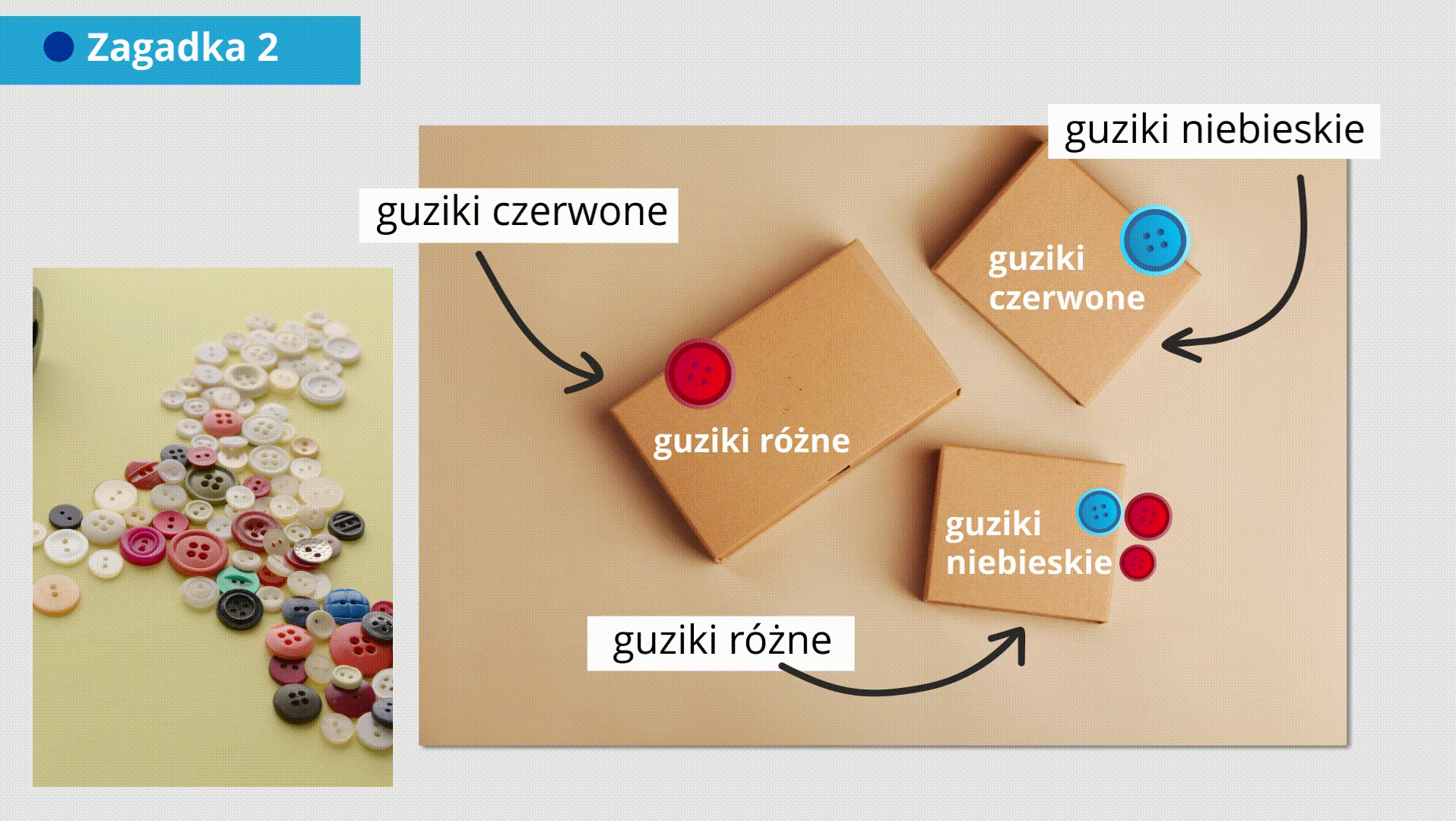
Lektor mówi: Teraz inna zagadka logiczna. W trzech zamkniętych pudełkach są guziki. W jednym są guziki czerwone, w drugim niebieskie, a w trzecim niebieskie i czerwone. Pudełka podpisane są: guziki czerwone, guziki niebieskie, guziki różne. Niestety, okazuje się, że na każdym pudełku jest fałszywy napis. Chcesz ustalić, w którym pudełku są jakiego koloru guziki. Ale możesz wyciągnąć tylko po omacku jeden guzik z jednego pudełka. Bez zaglądania do tego pudełka! Jak myślisz z którego pudełka trzeba wyciągnąć guzik?
Jeśli uważasz, że trzeba wyciągnąć guzik z pudełka z napisem guziki czerwone, to sięgając do tego pudełka możesz wyciągnąć na przykład guzik niebieski. Ale guzik niebieski może znajdować się w pudełku z guzikami niebieskimi lub z guzikami różnymi. Więc trzeba będzie jeszcze sięgnąć do innego pudełka.
Podobna sytuacja będzie, gdy z pudełka z napisem guziki niebieskie wyciągniesz guzik czerwony.
Na slajdzie przedstawione są trzy pudełka z podpisami guziki czerwone, guziki niebieskie oraz guziki różne. Wokół pudełek rozsypane są różne guziki.
Slajd czwarty:
Lektor mówi: Jedyna możliwość zatem, to wyciągnięcie guzika z pudełka z napisem guziki różne. Muszą tam być przecież guziki jednego koloru, bo napis na pudełku jest fałszywy.
Na slajdzie przedstawione są trzy pudełka z podpisami guziki czerwone, guziki niebieskie oraz guziki różne. Przy pudełku z napisem guziki różne są dwa punkty klikalne kolorem odpowiadające guzikom.
Punkt niebieski: Gdy wyciągniesz guzik niebieski – w tym pudełku są guziki niebieskie, w pudełku guziki niebieskie są guziki czerwone i w pudełku guziki czerwone są guziki różne.
Punkt czerwony podobnie, jeśli z pudełka guziki różne wyciągniesz guzik czerwony, to w tym pudełku są guziki czerwone, w pudełku oznaczonym guziki niebieskie są guziki różne, a w pudełku guziki czerwone są guziki niebieskie.
Slajd piąty:
Lektor mówi: Zagadka trzecia – również łatwa. Pani Pelagia codziennie wkłada nową suknię. W każdy poniedziałek zanosi brudne suknie do pralni i jednocześnie odbiera suknie wyprane. Ile co najmniej sukien ma pani Pelagia?
Na slajdzie znajduje się kobieta w sukience.
Obok punkt kilkalny, pod którym jest ukryte rozwiązanie. Lektor mówi: Ta zagadka to oczywiście żart. Tydzień ma siedem dni, więc pani Pelagia zanosi do pralni siedem sukien i siedem odbiera. Ale na sobie ma jeszcze jedną suknię. Siedem plus siedem plus jeden to piętnaście, więc pani Pelagia ma co najmniej piętnaście sukien.
Slajd szósty:
Lektor mówi: Przechodzimy do zagadek, których rozwiązanie będzie wymagało wykonywania prostych obliczeń.
Na slajdzie zapisano treść zadania. Masz do dyspozycji dwie liczby trzy i cztery. Oraz znaki działań dodawania oraz mnożenia. Zapisz za pomocą tych liczb oraz tych znaków działań, każdą z liczb: siedem, dwanaście, trzynaście, piętnaście, dziewiętnaście czterdzieści trzy oraz dwieście sześćdziesiąt pięć.
Obok punkt kilkalny, pod którym jest ukryte rozwiązanie. Lektor mówi: Zastanów się przez chwilę i porównaj z przykładowymi rozwiązaniami.
Slajd siódmy:
Lektor mówi: Zagadka piąta. Ewelina dostała na imieniny bombonierki z czekoladkami wiśniowymi i bombonierki z czekoladkami karmelowymi. Czekoladki wiśniowe pakowane były po dziewięć sztuk w jednej bombonierce, a czekoladki karmelowe po pięć sztuk w jednej bombonierce. Łącznie były sześćdziesiąt dwie czekoladki.
Na slajdzie przedstawiono grafikę z treścią zadania i zdjęciem dwóch pudełek z czekoladkami podpisanymi odpowiedni bombonierka z czekoladkami wiśniowymi i bombonierka z czekoladkami karmelowymi.
Slajd ósmy:
Lektor mówi: Ile było pudełek z czekoladkami wiśniowymi? Ile było czekoladek karmelowych?
Na slajdzie zostało zapisane rozwiązanie zagadki.
– liczba bombonierek z czekoladkami wiśniowymi
– liczba bombonierek z czekoladkami karmelowymi
Czekoladek wiśniowych było dziewięć razy , a karmelowych pięć razy . Łącznie były sześćdziesiąt dwie czekoladki.
Z zapisanego równania wyznaczymy .
Aby liczba k była liczbą naturalną, licznik ułamka zapisanego po prawej stronie równania, musi być liczbą podzielną przez pięć. A więc liczbą, której cyfra jedności to pięć lub zero. Za w podstawiamy kolejne liczby naturalne dodatnie, wykonujemy odejmowanie i sprawdzamy, czy otrzymamy liczbę, której cyfra jedności to pięć lub zero. Rozpatrzymy możliwe przypadki.
to - nie spełnia warunków zadania.
to - nie spełnia warunków zadania.
to - spełnia warunki zadania. Przypadek zostaje podkreślony falistą linią.
to - nie spełnia warunków zadania.
to - nie spełnia warunków zadania.
to - nie spełnia warunków zadania.
to - nie spełnia warunków zadania.
Zatem były trzy bombonierki z czekoladkami wiśniowymi i siedem z czekoladkami karmelowym. Czekoladek karmelowych było . Na slajdzie zapisano: .
Odpowiedź:
Były trzy bombonierki z czekoladkami wiśniowymi i siedem z czekoladkami karmelowymi. Czekoladek karmelowych było .
Slajd dziewiąty:
Lektor mówi: Teraz z pozoru prosta zagadka. Słoik z pokrywką kosztuje . Słoik jest o złotówkę droższy od pokrywki. Ile kosztuje słoik, a ile pokrywka? Wydaje się, że słoik kosztuje złotówkę, a pokrywka 10 groszy. Jednak nie jest to dobra odpowiedź. Jeśli bowiem pokrywka kosztowałaby groszy, to słoik kosztowałby (bo jest o złotówkę droższy od pokrywki). Zatem słoik z pokrywką kosztowałby .
Na slajdzie zapisano treść zadania: Słoik z pokrywką kosztuje . Słoik jest o złotówkę droższy od pokrywki. Ile kosztuje słoik, a ile pokrywka ? Pod treścią zadania, po prawej stronie umiezczono zdjęcie słoika.
Lektor mówi: Aby znaleźć poprawną odpowiedź, ułożymy i rozwiążemy odpowiednie równanie. Oznaczmy przez iks cenę pokrywki w groszach. Wtedy cena słoika jest równa groszy. A cena słoika z pokrywką groszy.
Treść czytana przez lektora zostaje zapisana pod treścią zadania po lewej stronie.
Lektor mówi: Otrzymujemy proste równanie, którego rozwiązaniem jest liczba pięć.
Na slajdzie pod oznaczeniami zapisano: ,
,
,
.
Lektor mówi: Zatem pokrywka kosztuje pięć groszy, a słoik sto pięć groszy. Na planszy pod obliczeniami zapisano .
Slajd dziesiąty:
Lektor mówi: Tym razem nie trzeba będzie zgadywać. Pokażemy, jak zbudować własny kwadrat magiczny. W tym celu posłużymy się znanym kwadratem magicznym o sumie równej piętnaście.
Na slajdzie przedstawiono dwa kwadraty magiczne trzy na trzy wypełniony liczbami.
Kawdrat po lewej stronie planszy.
Lektor mówi: W tym celu posłużymy się znanym kwadratem magicznym o sumie równej piętnaście.
W pierwszym rzędzie znajdują się liczby , , .
W drugimi rzędzie znajdują się liczby , , .
W trzecim rzędzie znajdują się liczby , , .
Oznaczono, że suma liczb w każdej kolumnie, każdym rzędzie oraz po przekątnej jest równa piętnoście.
Kawdrat po prawej stronie planszy.
Lektor mówi: Teraz od każdej z liczb zapisanych w kwadracie odejmiemy jakąś liczbę. Na przykład cztery. Okazuje się, że otrzymaliśmy kwadrat magiczny, o sumie magicznej równej trzy. I ty może utworzyć własny kwadrat, dodając, odejmując, mnożąc lub dzieląc każdą liczbę w danym kwadracie przez tą samą liczbę różną od zera.
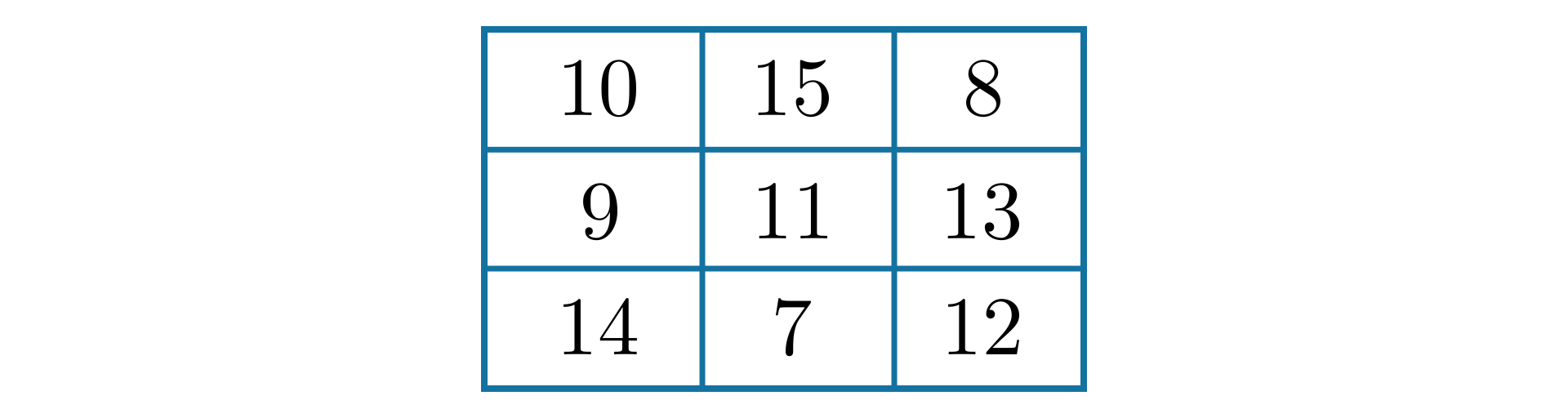
Na slajdzie przedstawiono kwadrat magiczny trzy na trzy wypełniony liczbami.
W pierwszym rzędzie znajdują się liczby , , .
W drugimi rzędzie znajdują się liczby , , .
W trzecim rzędzie znajdują się liczby , , .
Oznaczono, że suma liczb w każdej kolumnie, każdym rzędzie oraz po przekątnej jest równa trzy.
Slajd jedenasty:
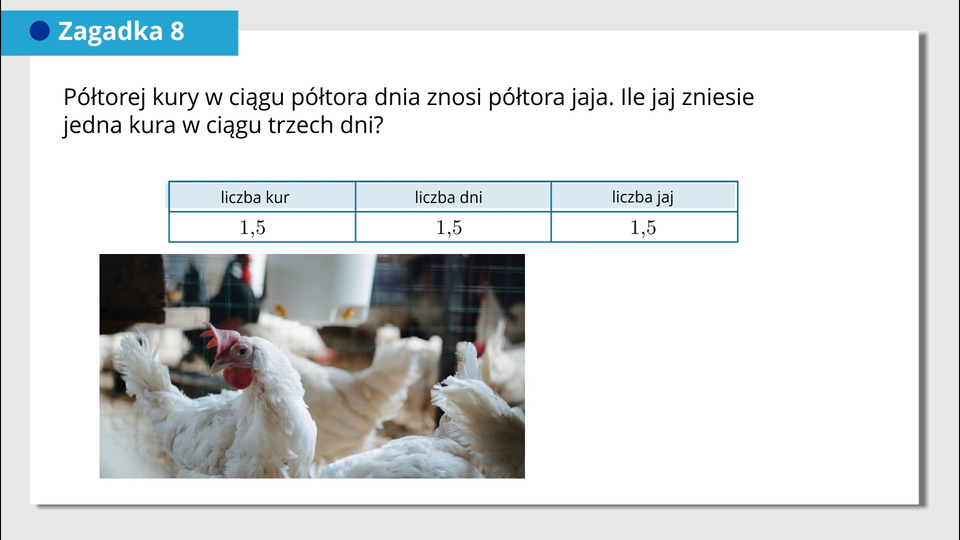
Lektor mówi: Teraz zadanie, którego podobno nie umie rozwiązać połowa dorosłych. Półtorej kury w ciągu półtora dnia znosi półtora jaja. Ile jaj zniesie jedna kura w ciągu trzech dni? Zapiszmy dane z zadania w tabelce. Na slajdzie zapisano treść zadania. Pod spodem umieszczono tabelę.
Liczba kur | Liczba dni | Liczba jaj |
|---|---|---|
Slajd dwunasty:
Lektor mówi: Zapiszmy dane z zadania w tabelce.
Na slajdzie rozszerzono tabelkę.
Liczba kur | Liczba dni | Liczba jaj | komentarz lektora |
|---|---|---|---|
brak komentarza | |||
Jeśli podwoimy liczbę kur, to zniosą one dwa razy więcej jaj w tym samym czasie. | |||
Wynika stąd, że 3 kury w ciągu jednego dnia zniosą 2 jaja. | |||
Czyli jedna kura w ciągu jednego dnia zniesie dwie trzecie jaja. | |||
I wreszcie mamy odpowiedź – jedna kura w ciągu trzech dni zniesie dwa jaja. |
Patryk zbierał grzyby. W domu okazało się, że wszystkich zebranych grzybów to grzyby robaczywe, połowa była niejadalnych, a ćwierć były to grzyby robaczywe i na dodatek niejadalne. Tylko dwa grzyby okazały się przydatne do spożycia.
Ile grzybów zebrał Patryk?
Przez mostek na rzeczce, drogi kolego, idą kaczki gęsiego.
Jedna na samym przedzie, za nią dwie maszerują,
Jedna z tyłu i dwie na początku plotkują.
Jedna pośrodku i trzy w jednym rzędzie.
Czy już wiesz, ile tych kaczek będzie?
W pudełku znajdują się klocki w różnych kolorach: niebieskim, zielonym, żółtym i czerwonym. Niebieskie i zielone klocki stanowią całego pudełka, żółte klocki stanowią pudełka i jest ich . Ile jest w pudełku klocków w kolorze czerwonym?
Jeśli i to ile jest równe ?
Jaką liczbę należy wpisać w miejsce znaku zapytania? Wskaż prawidłową odpowiedź.
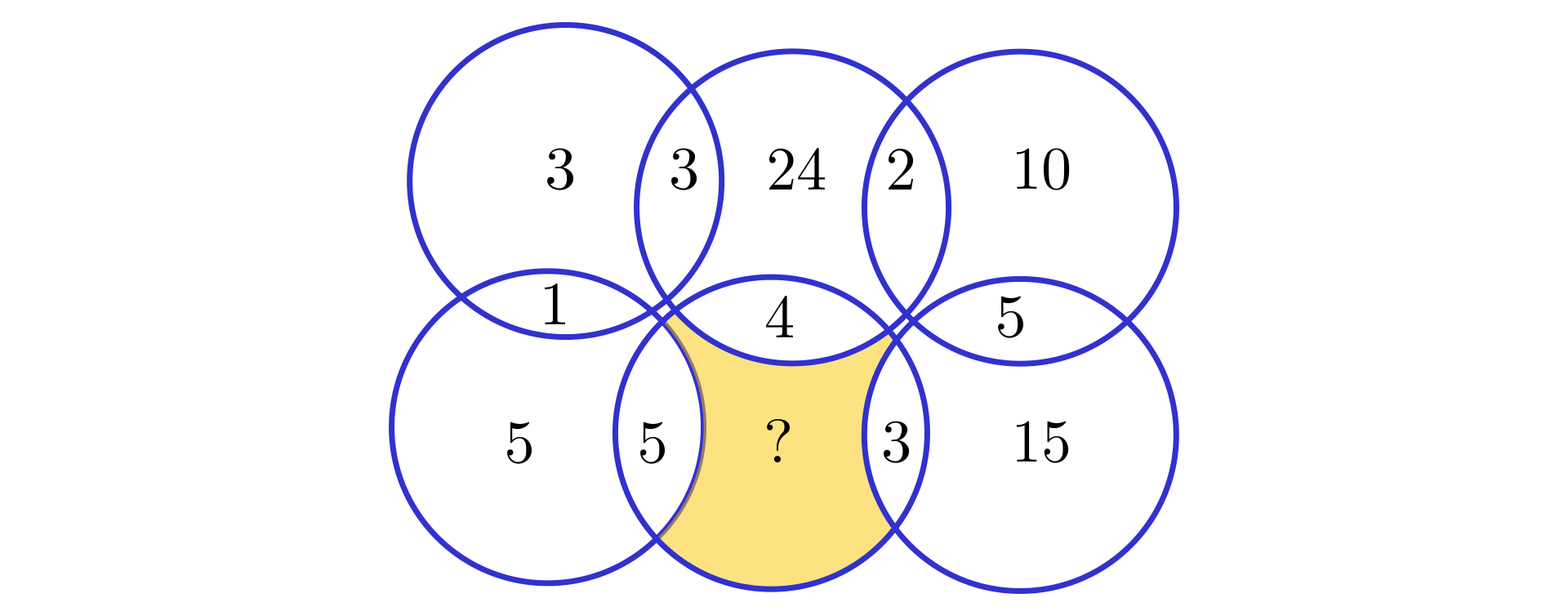
Która z poniższych liczb może być najmniejszą wspólną wielokrotnością tych liczb?
Liczba to liczby .
Liczba to liczby .
Liczba to liczby .
Zaznacz wszystkie nierówności prawdziwe. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Kolejne figury tworzone są poprzez „dobudowywanie” sześciokątów tak, jak na rysunku.
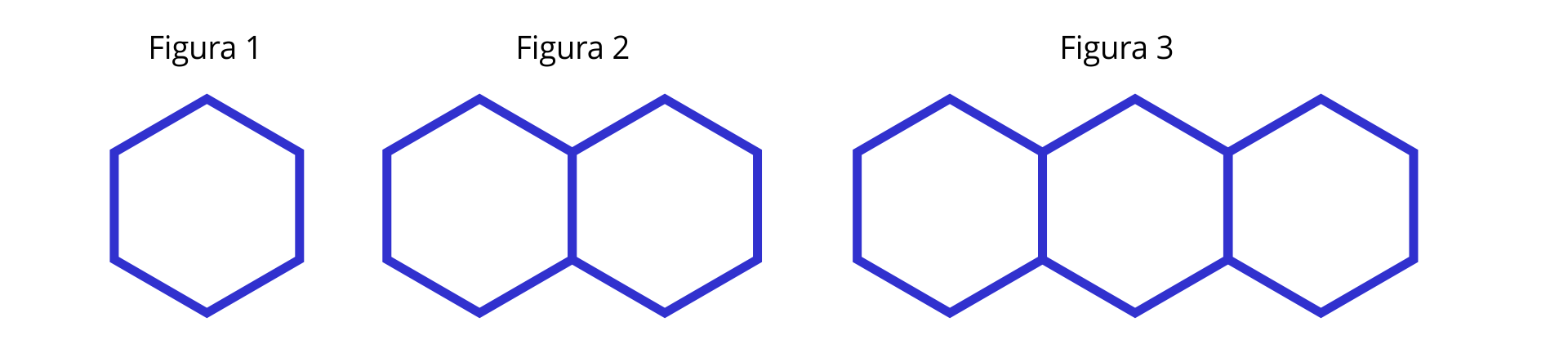
Zagadki Leonarda z Pizy:
Znajdź najmniejszą liczbę naturalną dodatnią, podzielną przez , która w dzieleniu przez , , , , daje resztę .
Znajdź najmniejszą liczbę naturalną dodatnią, podzielną przez , która w dzieleniu przez , , , , daje resztę odpowiednio , , , ,
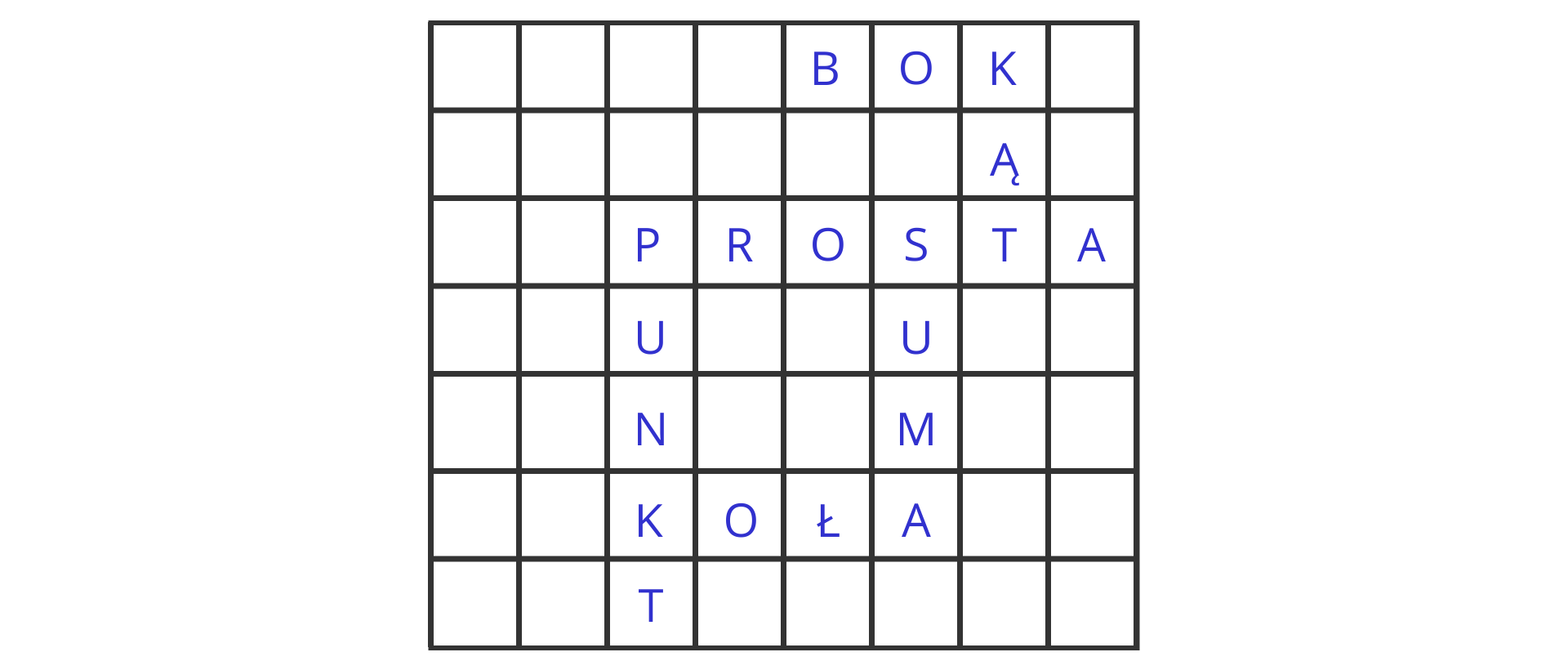
Wykreśl wyrazy oznaczające pojęcia matematyczne rozmieszczone w diagramie poziomo lub pionowo. Litery do wykreślenia mogą być użyte w kilku wyrazach.
Pozostałe litery, czytane poziomo, utworzą hasło. Odczytaj je.
Słownik
to kwadratowa tablica, w pola której wpisano liczby w ten sposób, że ich suma w każdym wierszu, w każdej kolumnie i na każdej przekątnej jest taka sama.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.