RUuR6qXpfQwFG
Ilustracja przedstawia ustawione w wielu rzędach sześciany wykonane z betonu.

Poznajemy bryły

Źródło: Christian Fregnan, dostępny w internecie: www.unsplash.com.

1. Opis prostopadłościanu i sześcianu

Sześcian jest bryłą, którą człowiek bardzo często wykorzystuje w budowlach i konstrukcjach. Wiele zabawek dziecięcych ma kształt sześcianu: klocki, układanki, kostki. Jego regularny kształt jest funkcjonalny i przydatny w rzeczywistości wykreowanej przez człowieka. Wydawać by się mogło, że bryła ta została stworzona przez człowieka i dla jego potrzeb. Nic bardziej mylnego. Przykładami sześciennych kształtów w naturze są niektóre kryształy, w tym znany nam kryształ chlorku sodu i pirytu.

RZGnKUOtKTSpF
Na ilustracji przedstawiono kryształ pirytu, który ma kształt sześcianu.
Piryt
Źródło: DidierDescouens, dostępny w internecie: commons.wikimedia.org, licencja: CC BY-SA 4.0.

Wielokąty, proste i odcinki to figury płaskie. Wokół nas znajdują się także obiekty przestrzenne. Niektóre kartoniki, pudełka i kostki mają kształt figur przestrzennych, o których jest ten materiał.
Obejrzyj poniższy film, aby poznać przykłady figur przestrzennych.

R12VIMpwN9V1P1
Animacja pokazuje podstawowe figury przestrzenne oraz sposób ich przedstawiania na płaszczyźnie.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R12VIMpwN9V1P

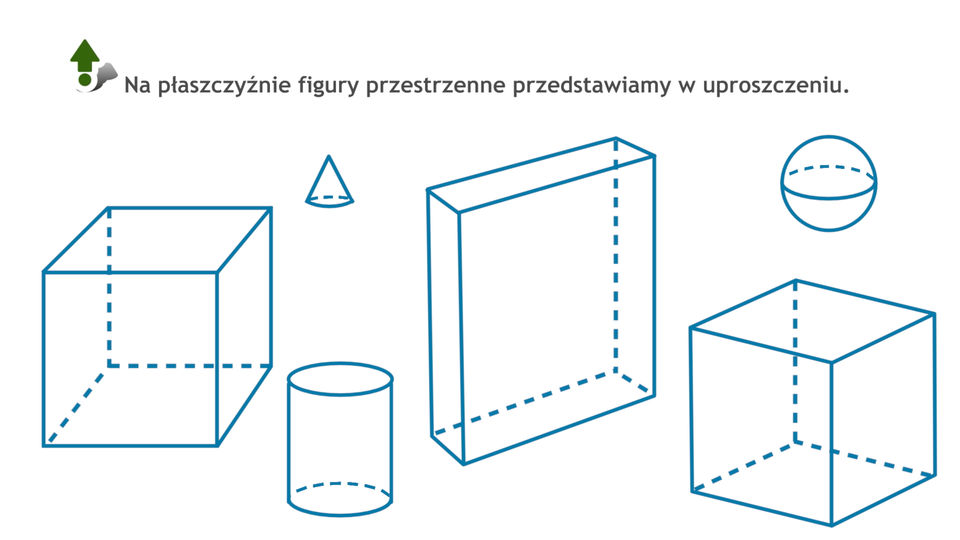
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja pokazuje podstawowe figury przestrzenne oraz sposób ich przedstawiania na płaszczyźnie.

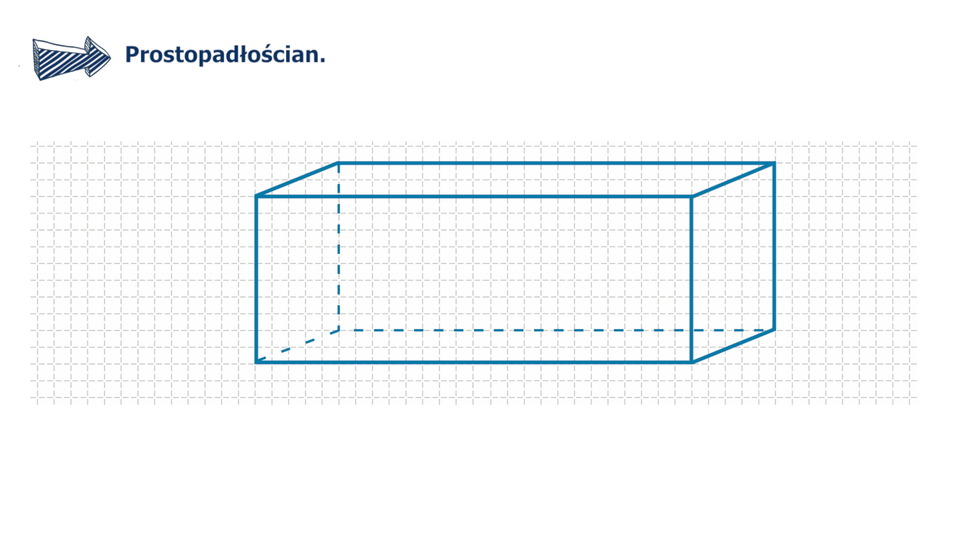
Jedną z figur przestrzennych jest prostopadłościan. Wszystkie ściany prostopadłościanu są prostokątami.

Zapoznaj się dokładnie z modelem prostopadłościanu.

R1XhttEbTbMMj1
Animacja przedstawia jakie bryły nazywamy prostopadłościanami.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1XhttEbTbMMj

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jakie bryły nazywamy prostopadłościanami.

Ważne!

  • Każdy prostopadłościan ma sześć ścian, które są prostokątami. Dwie z nich nazywamy podstawami, pozostałe to ściany boczne.

  • Boki prostokątów, które są ścianami prostopadłościanu, nazywamy krawędziami. Wśród nich są krawędzie podstawy i krawędzie boczne.

  • Punkty wspólne krawędzi to wierzchołki prostopadłościanu.

R1A31nxQgnfhd1
Rysunek prostopadłościanu. Na rysunku zaznaczono: wierzchołek, podstawę, krawędź podstawy, ścianę boczna, krawędź boczną. Kolorem niebieskim zamalowano wskazaną dolną podstawę oraz jedną ze ścian bocznych.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ważne!

W prostopadłościanie można wskazać krawędzie równoległe. Krawędzie, które są równoległe, mają tę samą długość.

RWFRIhUmF7H1a1
Rysunek prostopadłościanu. Na rysunku zaznaczono tymi samymi kolorami krawędzie jednakowej długości. Cztery najdłuższe krawędzie zaznaczono kolorem fioletowym. Cztery najkrótsze krawędzie zaznaczono kolorem zielonym. Cztery pozostałe krawędzie zaznaczono kolorem niebieskim. Krawędzie oznaczone tymi samymi kolorami względem siebie równoległe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Krawędzie zaznaczone tym samym kolorem są równej długości i są równoległe.

Ważne!

W prostopadłościanie krawędzie wychodzące z tego samego wierzchołka są prostopadłe.

RdnKZAU5M1kBh1
Rysunek prostopadłościanu. Na rysunku zaznaczono trzema różnymi kolorami, trzy krawędzie wychodzące z tego samego wierzchołka. Kolejno. Kolorem fioletowym, niebieskim oraz zielonym.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Krawędź zielona jest prostopadła do fioletowej.

Krawędź niebieska jest prostopadła do zielonej.

Krawędź niebieska jest prostopadła do fioletowej.

Ważne!

W prostopadłościanie można wskazać trzy pary ścian równoległych.

RSqVbA6XLZLXS1
Ilustracja przedstawia trzy prostopadłościany. W pierwszym prostopadłościanie kolorem niebieskim zamalowano równoległe do siebie podstawy prostopadłościanu, dolną oraz górną. W drugim prostopadłościanie kolorem fioletowym zamalowano równoległe do siebie dwie ściany boczne, przednią oraz tylną. W trzecim prostopadłościanie kolorem zielonym zamalowano dwie równoległe do siebie ściany boczne, lewą oraz prawą.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ściany zaznaczone tym samym kolorem są równoległe.

Ważne!

W prostopadłościanie każde sąsiadujące ze sobą ściany są prostopadłe.

R1IvhCxkXFn1V1
Rysunek trzech prostopadłościanów. W pierwszym zaznaczono ścianę boczną i podstawę dolną - są do siebie prostopadłe. W drugim zaznaczono ścianę tylną i podstawę dolną - są do siebie prostopadłe. W trzecim zaznaczono prawą ścianę boczną i ścianę tylną - są do siebie prostopadłe.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zamalowane ściany to przykłady ścian prostopadłych.

Ważne!

  • Z każdego wierzchołka prostopadłościanu wychodzą trzy krawędzie.

  • Długości tych krawędzi to wymiary prostopadłościanu, czyli długość, szerokość i wysokość.

R1JhNYUO7bLxc1
Rysunek prostopadłościanu z zaznaczonymi długościami krawędzi a, b, c wychodzącymi z jednego wierzchołka. a to długość, b to szerokość, c to wysokość.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zapoznaj się z poniższym filmem, który pokazuje, w jaki sposób narysować prostopadłościan.

R1HasuVOrxoKP1
Animacja przedstawia w jaki sposób możemy narysować prostopadłościan.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny pod adresem /preview/resource/R1HasuVOrxoKP

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia w jaki sposób możemy narysować prostopadłościan.

Sześcian
Definicja: Sześcian

Prostopadłościan, którego wszystkie krawędzie są równe, to sześcian. Każda ściana sześcianu jest kwadratem.

RN1aHWrqjRchw1
Animacja przedstawia jakie bryły nazywamy sześcianami.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

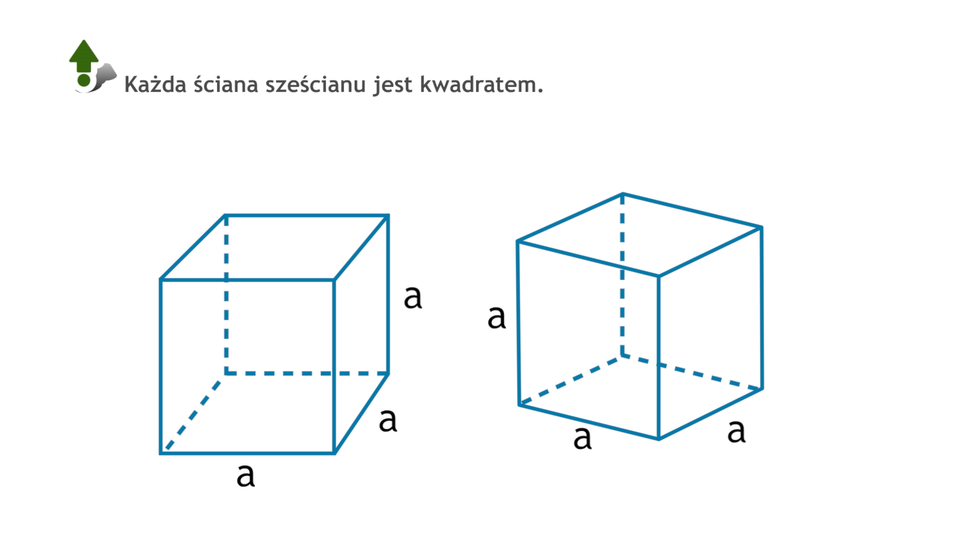
Film dostępny pod adresem /preview/resource/RN1aHWrqjRchw

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Animacja przedstawia jakie bryły nazywamy sześcianami.

Ćwiczenie 1

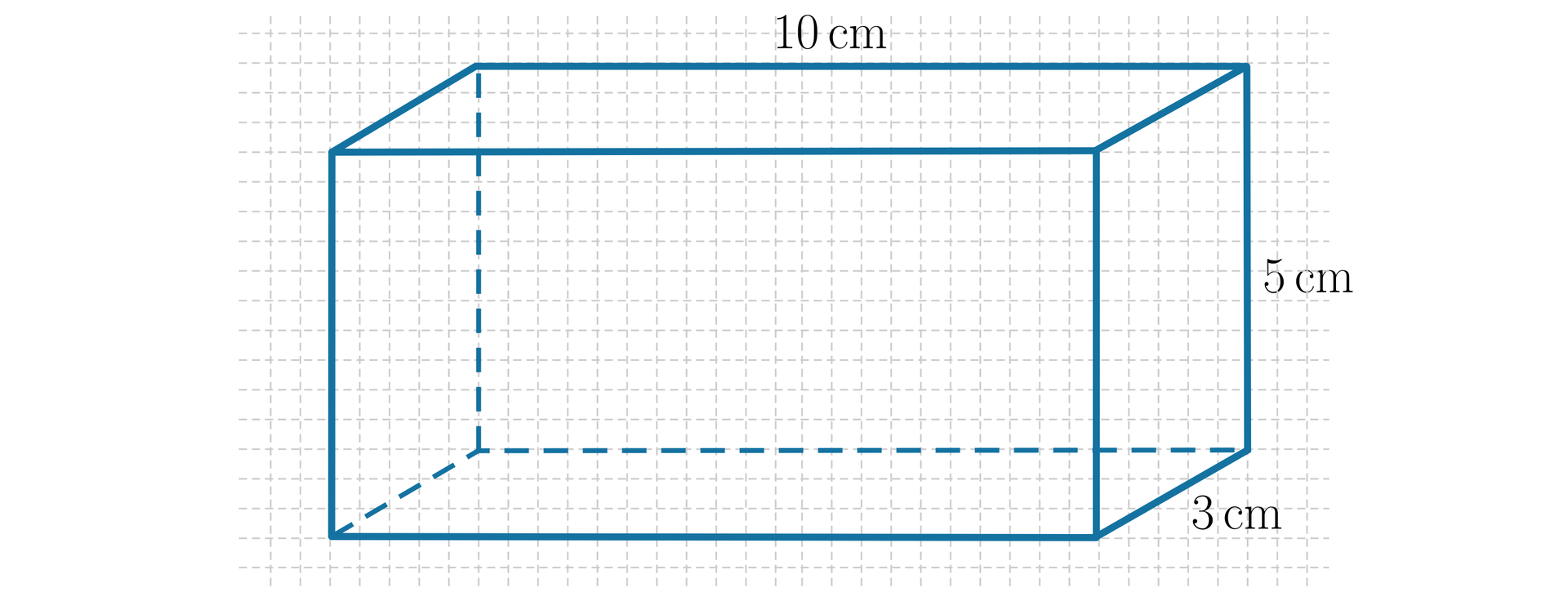
Zapoznaj się z poniższym rysunkiem prostopadłościanu ABCDEFGH.

R10xiUq4Rt31v1
Na rysunku przedstawiono prostopadłościan o dolnej podstawie A B C D oraz górnej E F G H. Odpowiednio nad wierzchołkiem A, znajduje się wierzchołek E. Nad wierzchołkiem B wierzchołek F. Nad wierzchołkiem C wierzchołek G. Nad wierzchołkiem D wierzchołek G.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R8Fp1DjtW8wyS1
Uzupełnij luki nazwami wierzchołków, krawędzi i ścian. Przeciągnij w nie odpowiednie elementy, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Pola uzupełniaj w kolejności alfabetycznej. wierzchołki: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG i 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
krawędzie boczne: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
krawędzie podstawy dolnej: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
krawędzie podstawy górnej: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG, 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
ściany boczne: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG,1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
podstawa dolna:1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG;
podstawa górna: 1. ABFE, 2. BF, 3. DCGH, 4. H, 5. FG, 6. DA, 7. HE, 8. EFGH, 9. GH, 10. CD, 11. AE, 12. B, 13. DH, 14. F, 15. A, 16. ABCD, 17. D, 18. ADHE, 19. AB, 20. BC, 21. EF, 22. BCGF, 23. E, 24. G, 25. C, 26. CG.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 2

Zapoznaj się z poniższym rysunkiem prostopadłościanu MIROSŁAW.

R1J6AG7UF3bm11
Ilustracja przedstawia prostopadłościan o dolnej podstawie M I R O oraz o górnej podstawie S Ł A W. Ściany boczne tej figury to S M O W, A R I Ł, A R O W i M I Ł S.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R13IxbjOFGp2f
Uzupełnij luki nazwami wierzchołków, krawędzi i ścian. Przeciągnij w nie odpowiednie elementy, lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Pola uzupełniaj w kolejności alfabetycznej. wierzchołki: 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM;krawędzie boczne: 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM;krawędzie podstawy dolnej: 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM, 1. M, 2. O, 3. R, 4. MS, 5. A, 6. W, 7. RO, 8. Ł, 9. MI, 10. IR, 11. S, 12. IŁ, 13. OW, 14. I, 15. RA, 16. OM.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 3

Policz, ile jest krawędzi o długości 3 dm i oblicz ich łączną długość. Postępuj tak samo z pozostałymi krawędziami. Oblicz łączną długość wszystkich krawędzi narysowanego prostopadłościanu.

RSpAZszUfm4bD1
Rysunek prostopadłościanu o podstawie będącej prostokątem o wymiarach 3 decymetry na 1 decymetr i o wysokości 2 decymetry.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R1Db1Uz02TtYs1
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 4

Narysuj przykładowy prostopadłościan.

R11KMCSwga2RC1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Opisz sposób rysowania przykładowego prostopadłościanu.

Ćwiczenie 5
RNjKzCPfWL7je1
Jaka jest suma długości wszystkich krawędzi prostopadłościanu o wymiarach 8 cm, 5 cm i 9 cm? Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Suma długości wszystkich krawędzi tego prostopadłościanu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 6
Rs4lPx1sEpC6u1
Suma długości wszystkich krawędzi prostopadłościanu wynosi 120 cm. Jaką długość ma wysokość tego prostopadłościanu, jeśli jego podstawą jest prostokąt o bokach 10 cm i 12 cm? Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Wysokość tego prostopadłościanu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 7
RZQRTSF6YIO0K
Przypomnij sobie tytuł abstraktu, wysłuchaj nagrania i spróbuj zaproponować własny temat dla dzisiejszej lekcji.

  • 67594
  • 67461
  • 67460
  • 67462
  • 67463
  • 67464
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R10mbHWQssmOS1
Wybierz te przedmioty, które standardowo mają kształt prostopadłościanu. Zaznacz wszystkie prawidłowe odpowiedzi. Możliwe odpowiedzi: 1. pudełko zapałek, 2. pudełko po butach, 3. kostka Rubika, 4. kostka do gry mająca sześć oczek, 5. klepsydra, 6. puszka napoju, 7. butelka
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 8

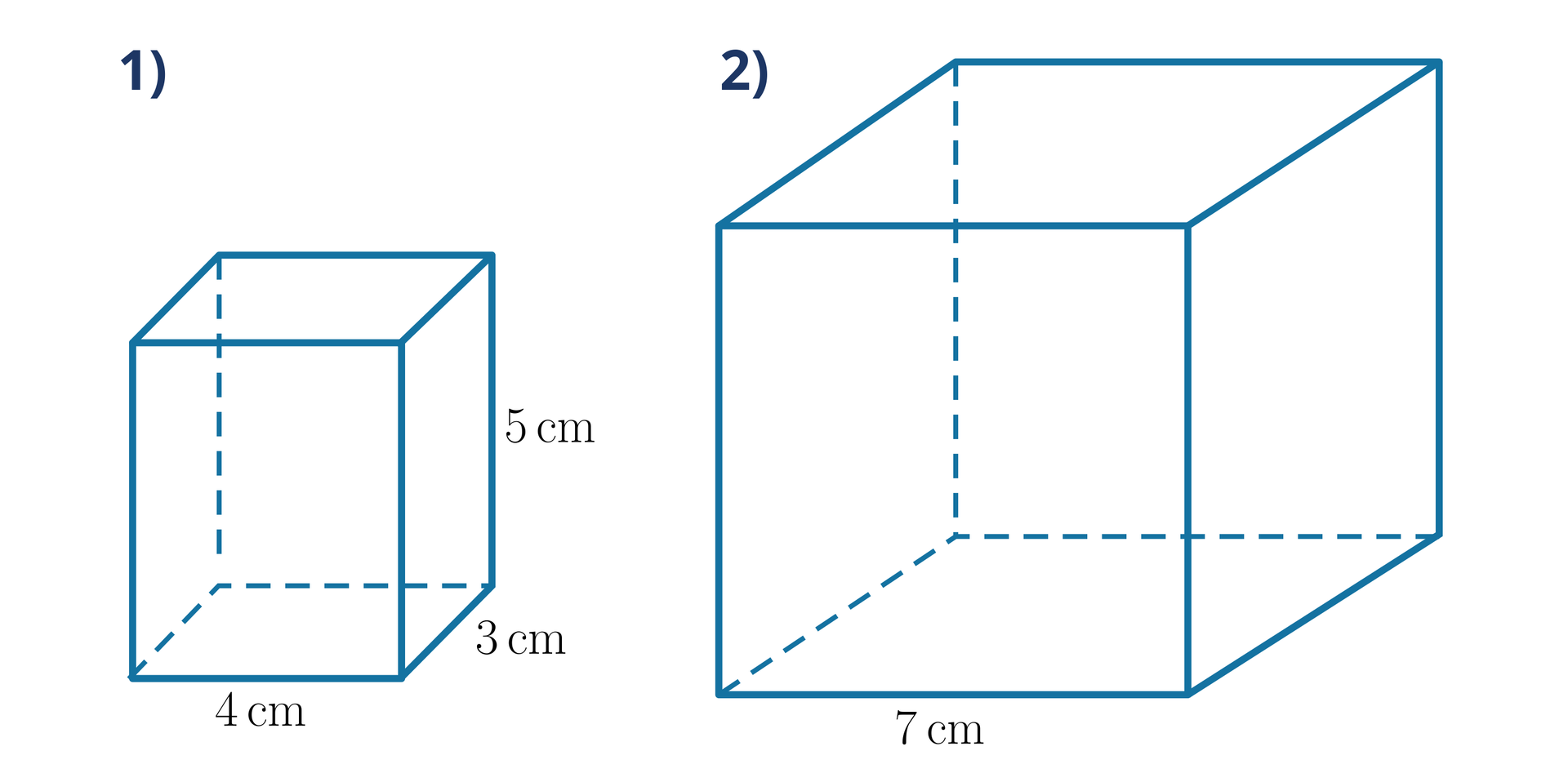
Oblicz łączną długość wszystkich krawędzi sześcianu przedstawionego na poniższym rysunku.

ROJw39RlQNVY21
Rysunek sześcianu o krawędzi długości 5 decymetrów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R15lYEEfKlAur1
Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Długość wszystkich krawędzi tego sześcianu wynosi Tu uzupełnij dm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 9
R1SxBpYjYVUay1
Krawędź sześcianu ma długość 17 cm. Oblicz sumę długości wszystkich krawędzi tego sześcianu. Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Długość wszystkich krawędzi tego sześcianu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 10
R1HdkXVZVE2F11
Suma długości wszystkich krawędzi sześcianu wynosi 72 cm. Jaką długość ma krawędź tego sześcianu? Uzupełnij odpowiedź, wpisując w lukę odpowiednią liczbę. Odpowiedź: Długość krawędzi tego sześcianu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 11
RcSfhgS6VKGbI1
Suma długości wszystkich krawędzi sześcianu wynosi 2,4 m. Jaką długość ma krawędź tego sześcianu? Odpowiedź wpisz w pustą lukę. Odpowiedź: Długość krawędzi tego sześcianu wynosi Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 12

Narysuj

  1. prostopadłościan, którego krawędzie mają długość 3 cm, 4 cm, 5 cm,

  2. sześcian, którego suma krawędzi wynosi 84 cm.

R11KMCSwga2RC1
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Zosia chce wykorzystać całe 90 cm drucika na zbudowanie jednego prostopadłościanu oraz jednego sześcianu. Jakie długości krawędzi może mieć prostopadłościan, jeżeli suma krawędzi sześcianu jest równa 42 cm?

RBijH48QoBop41
Ćwiczenie 13
Zaznacz wszystkie zdania prawdziwe. Możliwe odpowiedzi: 1. Prostopadłościan ma trzy pary ścian równoległych., 2. Każdy prostopadłościan jest sześcianem., 3. Ściany sześcianu są jednakowymi kwadratami., 4. Każdy prostopadłościan ma wszystkie krawędzie równej długości., 5. Ściany prostopadłościanu mające wspólną krawędź są prostopadłe., 6. Każdy sześcian jest prostopadłościanem.

  • Prostopadłościan ma trzy pary ścian równoległych.
  • Każdy prostopadłościan jest sześcianem.
  • Ściany sześcianu są jednakowymi kwadratami.
  • Każdy prostopadłościan ma wszystkie krawędzie równej długości.
  • Ściany prostopadłościanu mające wspólną krawędź są prostopadłe.
  • Każdy sześcian jest prostopadłościanem.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 14
RFRBzA7PdUQKP
Jedna ściana prostopadłościanu jest kwadratem o boku 8 cm, a jedna z krawędzi tego prostopadłościanu ma długość 14 cm. Jakie wymiary ma ściana niebędąca kwadratem? Uzupełnij odpowiedź, wpisując w luki odpowiednie liczby. Odpowiedź: Dłuższy wymiar tej ściany to Tu uzupełnij cm, a krótszy to Tu uzupełnij cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Ćwiczenie 15
RZS5jkL3xXFnf1
Zaznacz te prostokąty, które mogą być ścianami tego samego prostopadłościanu.

  • 13825
  • 13826
  • 13827
Źródło: GroMar, licencja: CC BY 3.0.
RwBb7Pu1tBJ7a
Zaznacz wszystkie prostokąty, które mogą być ścianami tego samego prostopadłościanu. Możliwe odpowiedzi: 1. Prostokąt o wymiarach 6 cm na 4 cm., 2. Prostokąt o wymiarach 4 cm na 3 cm., 3. Prostokąt o wymiarach 5 cm na 7 cm.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
R3XrikIQDcUbj1
Ćwiczenie 16
Z sześcianów o krawędzi 4 cm budowano prostopadłościany. Ile sześcianów użyto do zbudowania prostopadłościanu o podanych krawędziach? Wpisz w wyznaczone miejsca brakujące liczby. Do zbudowania prostopadłościanu o krawędziach długości 4 cm, 4 cm, 8 cm użyto Tu uzupełnij takie sześciany.Do zbudowania prostopadłościanu o krawędziach długości 4 cm, 8 cm, 8 cm użyto Tu uzupełnij takie sześciany.Do zbudowania prostopadłościanu o krawędziach długości 4 cm, 8 cm, 12 cm użyto Tu uzupełnij takich sześcianów.Do zbudowania prostopadłościanu o krawędziach długości 8 cm, 8 cm, 12 cm użyto Tu uzupełnij takich sześcianów.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3
(Uzupełnij).
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Powtórzenie - Proste wyrażenia algebraiczne
2. Własności prostopadłościanów i sześcianów