Stosowanie wyrażeń algebraicznych
4. Dodawanie i odejmowanie sum algebraicznych
Po podwórku chodzą gęsi, kaczki i kury. Kur jest o więcej niż kaczek. Gęsi jest o mniej niż kur. Ile wszystkich ptaków chodzi po podwórku?

Z treści zadania nie można wywnioskować, ile kaczek chodzi po podwórku. Oznaczymy więc liczbę kaczek literą .
Wtedy liczba kur jest równa , a liczba gęsi .

Liczbę wszystkich ptaków chodzących po podwórku zapisujemy za pomocą wyrażenia algebraicznego:
Wyrażenie to możemy zapisać w prostszej postaci, wykonując redukcję wyrazów podobnych.
Wyrażenie, które przekształciliśmy, to suma algebraicznasuma algebraiczna.
Sumą algebraiczną nazywamy sumę jednomianów.
Jednomiany, które dodajemy to wyrazy sumy.
Wyrazy podobne występujące w sumie algebraicznej można redukować.
Tabelka przedstawia sumy algebraiczne i wyrazy tych sum.
Suma algebraiczna | Wyrazy sumy |
|---|---|
, , | |
, , , | |
, , |
Odejmowanie można zastąpić dodawaniem liczby przeciwnej, zatem sumą algebraicznąsumą algebraiczną jest też różnica jednomianówjednomianów.
Zapiszemy w najprostszej postaci wyrażenie .
Grupujemy wyrazy podobne i wykonujemy dodawanie.
Zapiszemy za pomocą wyrażenia algebraicznego:
sumę czterech kolejnych liczb naturalnych,
sumę czterech kolejnych liczb naturalnych nieparzystych,
sumę czterech kolejnych liczb naturalnych podzielnych przez trzy.
Rozwiązanie:
Oznaczmy przez najmniejszą z rozważanych liczb naturalnych. Kolejne liczby naturalne różnią się o .
Wtedy:
– pierwsza liczba naturalna,
– druga liczba naturalna,
– trzecia liczba naturalna,
– czwarta liczba naturalna.
Suma liczb:
.sposób:
Oznaczmy przez najmniejszą z rozważanych liczb nieparzystych naturalnych. Kolejne liczby różnią się o .
Zatem:
– pierwsza liczba nieparzysta,
– druga liczba nieparzysta,
– trzecia liczba nieparzysta,
– czwarta liczba nieparzysta.
Suma liczb:
.
sposób:
Kolejne liczby nieparzyste to: , , , , , Są to liczby, które przy dzieleniu przez dają resztę .
Oznaczmy przez dowolną liczbę naturalną dodatnią. Wtedy cztery kolejne liczby nieparzyste można zapisać w postaci:
, , , .
Suma liczb:
.sposób:
Oznaczmy przez pierwszą z rozważanych liczb podzielnych przez . Kolejne liczby podzielne przez różnią się o .
Wtedy:
– pierwsza liczba podzielna przez trzy,
– druga liczba podzielna przez trzy,
– trzecia liczba podzielna przez trzy,
– czwarta liczba podzielna przez trzy.
Suma liczb:
.
sposób:
Kolejne liczby naturalne podzielne przez trzy to: , , , , , Są to kolejne wielokrotności liczby trzy.
Oznaczmy przez dowolną liczbę naturalną.
Wtedy cztery kolejne wielokrotności liczby trzy można zapisać w postaci: , , , .
Suma liczb:
.
Zapiszemy w najprostszej postaci wyrażenie algebraiczne, stanowiące odpowiedź do poniższego zadania.
W sadzie rosną grusze, śliwy, jabłonie i czereśnie. Grusz jest dwa razy więcej niż śliw, jabłoni jest tyle ile grusz i śliw razem. Czereśni rosło początkowo trzy razy tyle ile pozostałych drzew.
Niestety wichura zniszczyła pięć czereśni.
Obliczymy, ile co najmniej wszystkich drzew rośnie teraz w sadzie.
Oznaczymy przez liczbę śliw rosnących w ogrodzie, przez liczbę wszystkich drzew rosnących w ogrodzie. Potrzebne dane zamieścimy w tabelce.
Liczba rosnących teraz w ogrodzie: | |||
|---|---|---|---|
śliw | grusz | jabłoni | czereśni |
Aby obliczyć ile wszystkich drzew rośnie w ogrodzie, dodajemy liczbę rosnących tam śliw, grusz, jabłoni i czereśni.
Redukujemy wyrazy podobne i wykonujemy dodawanie w nawiasie.
Najmniejszą liczbą naturalną dodatnią jest jeden.
Odpowiedź:
W sadzie rośnie co najmniej drzew.
Sumy algebraiczne można dodawać i odejmować. Aby dodać dwie sumy algebraiczne, zapisujemy je w nawiasach, między którymi stawiamy znak plus. Opuszczamy nawiasy i redukujemy wyrazy podobne.
Jeżeli przed nawiasem, w którym zapisana jest suma algebraicznasuma algebraiczna stoi znak plus (lub nie ma żadnego znaku), to opuszczając nawias, znaki w nawiasie pozostawiamy bez zmiany.
Niech i . Zapiszemy w najprostszej postaci wyrażenie
Opuszczamy nawiasy (nie zmieniając znaków!) i redukujemy wyrazy podobne.
Odejmując dwie sumy algebraiczne postępujemy podobnie, jak przy dodawaniu sum algebraicznych. Sumy zapisujemy w nawiasach, między którymi stawiamy znak minus. Opuszczając nawias – zmieniamy znaki na przeciwne w sumie, którą odejmujemy.
Odejmując dwie sumy algebraiczne, w sumie, przed którą stoi znak minus, opuszczając nawias, zmieniamy znaki na przeciwne.
Niech i . Zapiszemy w najprostszej postaci wyrażenie .
Opuszczając nawiasy, zmieniamy znaki w wyrażeniu na przeciwne.
Redukujemy wyrazy podobne.
Krystian wybrał się rowerem z miejscowości Pojutrze do miejscowości Przedwczoraj, oddalonej o . Pierwszego dnia przejechał , drugiego dnia , a pozostałą część drogi przebył trzeciego dnia.
Obliczymy, ile kilometrów przejechał Krystian trzeciego dnia.
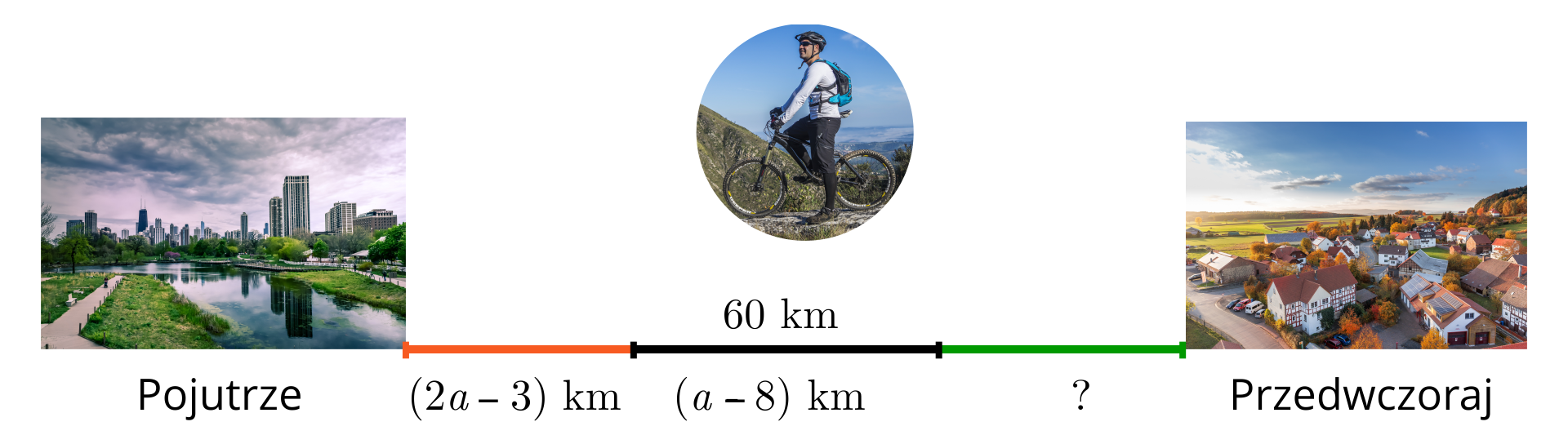
Pierwszego i drugiego dnia Krystian przejechał łącznie .
Zatem do przejechania zostało mu
.
Zapiszemy otrzymane wyrażenie w najprostszej postaci. Najpierw wykonujemy działania w nawiasie kwadratowym.
Przed nawiasem stoi znak minus – opuszczając nawias, zmieniamy znaki w nawiasie na przeciwne.
Odpowiedź:
Krystian trzeciego dnia przejechał .
Gra edukacyjna
Sprawdź swoje umiejętności dodawania i odejmowania wyrażeń algebraicznych. Zagraj w grę i postaraj się wydostać z pułapki. Pamiętaj, aby przed zapisaniem wyniku obliczeń zredukować wyrazy podobne.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1EFrD4UP
Etap pierwszy:
Etap drugi:
Zapisz wyrażenie w najprostszej postaci.
Zapisz wyrażenie w najprostszej postaci i oblicz wartość wyrażenia dla i .
Tadek ma lat. Mama Tadka jest dwa razy starsza, a tato jest o lata starszy od mamy. Ile lat będą mieli łącznie za dwa lata?
Jeżeli przed nawiasem, w którym występuje suma algebraiczna, znajduje się znak plus lub nie ma żadnego znaku, to usuwając nawias, nie zmieniamy znaków przed wyrazami sumy.
Jeżeli przed nawiasem, w którym występuje suma algebraiczna, znajduje się znak minus, to usuwając nawias, zmieniamy znak każdego z wyrazów sumy na przeciwny.
Czwarta zapisana przez niego czwarta liczba to: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Wskaż każde zdanie prawdziwe. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5.
Połącz każde z wyrażeń z odpowiadającym mu wyrażeniem otrzymanym po wykonaniu wskazanych działań i redukcji wyrazów podobnych. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5. Możliwe odpowiedzi: 1. , 2. , 3. , 4. , 5.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
Zaznacz, które stwierdzenie jest prawdziwe, a które fałszywe.. Basia ma teraz cukierki.. Możliwe odpowiedzi: Prawda, Fałsz. Adam ma teraz co najmniej sześć cukierków.. Możliwe odpowiedzi: Prawda, Fałsz. Adam ma teraz mniej cukierków niż Basia.. Możliwe odpowiedzi: Prawda, Fałsz. Basia i Adam mają teraz razem cukierków.. Możliwe odpowiedzi: Prawda, Fałsz
Ewa jest o lata młodsza od Jurka i razy starsza od Pawła, który ma lat.
Zapisz wyrażenia, które opisuje ile lat mieli razem Ewa, Jurek i Paweł lata temu.
Zapisz wyrażenie, które opisuje, ile lat będą mieli razem Ewa, Jurek i Paweł za lata.
Dorota kupiła jabłek w cenie za kilogram, gruszek w cenie za kilogram i kilogramy śliwek w cenie za kilogram. Dała kasjerce banknot stuzłotowy. Ile złotych reszty otrzymała?
Czy nawias został poprawnie usunięty?
Zaznacz, w których przykładach nawias został poprawnie usunięty?
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
Połącz w pary takie same sumy algebraiczne.
<span aria-label="nawias, x, plus, dwa y, zamknięcie nawiasu, minus, nawias z, minus, w zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mi>x</mi> <mo>+</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mi>z</mi> <mo>-</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label="nawias, minus, x, plus, dwa y, zamknięcie nawiasu, minus, nawias, minus, z, plus, w zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mo>-</mo> <mi>x</mi> <mo>+</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mo>-</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label="nawias, minus, x, plus, dwa y, zamknięcie nawiasu, plus, nawias z, plus, w zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mo>-</mo> <mi>x</mi> <mo>+</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label=" minus, nawias, x, minus, dwa y, zamknięcie nawiasu, plus, nawias, minus, z, plus, w zamknięcie nawiasu" role="math"><math> <mo>-</mo> <mfenced> <mrow> <mi>x</mi> <mo>-</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mo>-</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label="nawias, x, minus, dwa y, zamknięcie nawiasu, minus, nawias z, minus, w zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mi>x</mi> <mo>-</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mi>z</mi> <mo>-</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label=" minus, nawias, minus, x, minus, dwa y, zamknięcie nawiasu, minus, nawias z, plus, w zamknięcie nawiasu" role="math"><math> <mo>-</mo> <mfenced separator=""> <mrow> <mo>-</mo> <mi>x</mi> <mo>-</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label="nawias, minus, x, minus, dwa y, zamknięcie nawiasu, plus, nawias, minus, z, plus, w zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mo>-</mo> <mi>x</mi> <mo>-</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mo>-</mo> <mi>z</mi> <mo>+</mo> <mi>w</mi> <mo>)</mo> </math></span>, <span aria-label=" minus, nawias, minus, x, plus, dwa y, zamknięcie nawiasu, minus, nawias, minus, z, minus, w zamknięcie nawiasu" role="math"><math> <mo>-</mo> <mfenced separators=""> <mrow> <mo>-</mo> <mi>x</mi> <mo>+</mo> <mn>2</mn> <mi>y</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mo>-</mo> <mi>z</mi> <mo>-</mo> <mi>w</mi> <mo>)</mo> </math></span>
Wyrażenie po usunięciu nawiasów i redukcji wyrazów podobnych jest równe
Połącz w pary takie same sumy algebraiczne.
<span aria-label="nawias, minus, pięć a, minus, dwa b, zamknięcie nawiasu, plus, nawias, minus, a, minus, b zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mo>-</mo> <mn>5</mn> <mi>a</mi> <mo>-</mo> <mn>2</mn> <mi>b</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mo>-</mo> <mi>a</mi> <mo>-</mo> <mi>b</mi> <mo>)</mo> </math></span>, <span aria-label="a, plus, trzy b, minus, nawias, minus, dwa a, minus, dwa b zamknięcie nawiasu" role="math"><math> <mi>a</mi> <mo>+</mo> <mn>3</mn> <mi>b</mi> <mo>-</mo> <mo>(</mo> <mo>-</mo> <mn>2</mn> <mi>a</mi> <mo>-</mo> <mn>2</mn> <mi>b</mi> <mo>)</mo> </math></span>, <span aria-label="dwa a, plus, nawias, minus, cztery a, plus, sześć b, zamknięcie nawiasu, plus, nawias, minus, osiem b, minus, a zamknięcie nawiasu" role="math"><math> <mn>2</mn> <mi>a</mi> <mo>+</mo> <mfenced separators=""> <mrow> <mo>-</mo> <mn>4</mn> <mi>a</mi> <mo>+</mo> <mn>6</mn> <mi>b</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mo>-</mo> <mn>8</mn> <mi>b</mi> <mo>-</mo> <mi>a</mi> <mo>)</mo> </math></span>, <span aria-label=" minus, nawias, minus, trzy a, plus, b, zamknięcie nawiasu, minus, nawias trzy b, plus, a zamknięcie nawiasu" role="math"><math> <mo>-</mo> <mfenced separators=""> <mrow> <mo>-</mo> <mn>3</mn> <mi>a</mi> <mo>+</mo> <mi>b</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mn>3</mn> <mi>b</mi> <mo>+</mo> <mi>a</mi> <mo>)</mo> </math></span>, <span aria-label=" minus, nawias, dwa a, minus, trzy b, zamknięcie nawiasu, minus, nawias, minus, a, plus, dwa b zamknięcie nawiasu" role="math"><math> <mo>-</mo> <mfenced separators=""> <mrow> <mn>2</mn> <mi>a</mi> <mo>-</mo> <mn>3</mn> <mi>b</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mo>-</mo> <mi>a</mi> <mo>+</mo> <mn>2</mn> <mi>b</mi> <mo>)</mo> </math></span>, <span aria-label="dziesięć a, minus, nawias, siedem a, plus, b, zamknięcie nawiasu, minus, trzy b" role="math"><math> <mn>10</mn> <mi>a</mi> <mo>-</mo> <mfenced separators=""> <mrow> <mn>7</mn> <mi>a</mi> <mo>+</mo> <mi>b</mi> </mrow> </mfenced> <mo>-</mo> <mn>3</mn> <mi>b</mi> </math></span>, <span aria-label="nawias, a, plus, b, zamknięcie nawiasu, plus, nawias dwa a, minus, trzy b zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mi>a</mi> <mo>+</mo> <mi>b</mi> </mrow> </mfenced> <mo>+</mo> <mo>(</mo> <mn>2</mn> <mi>a</mi> <mo>-</mo> <mn>3</mn> <mi>b</mi> <mo>)</mo> </math></span>, <span aria-label="nawias, a, minus, trzy b, zamknięcie nawiasu, plus, nawias, minus, a, plus, trzy b, zamknięcie nawiasu, minus, nawias a, plus, trzy b zamknięcie nawiasu" role="math"><math> <mfenced separators=""> <mrow> <mi>a</mi> <mo>-</mo> <mn>3</mn> <mi>b</mi> </mrow> </mfenced> <mo>+</mo> <mfenced separators=""> <mrow> <mo>-</mo> <mi>a</mi> <mo>+</mo> <mn>3</mn> <mi>b</mi> </mrow> </mfenced> <mo>-</mo> <mo>(</mo> <mi>a</mi> <mo>+</mo> <mn>3</mn> <mi>b</mi> <mo>)</mo> </math></span>
Wyrażenie po usunięciu nawiasów i redukcji wyrazów podobnych jest równe
Zapisz każdą sumę algebraiczną w najprostszej postaci. Zaznacz równe sumy.
Zapisz każdą z sum algebraicznych w najprostszej postaci. Zaznacz równe sumy.
Zapisz każdą z sum algebraicznych w najprostszej postaci. Zaznacz równe sumy.
Rozstrzygnij, czy podana równość jest prawdziwa, czy fałszywa.
- 1
Połącz sumę algebraiczną i odpowiadającą jej uproszczoną postać.
<span aria-label=" minus, a, plus, dwa b" role="math"><math> <mo>-</mo> <mi>a</mi> <mo>+</mo> <mn>2</mn> <mi>b</mi> </math></span>, <span aria-label=" minus, dwa a, minus, b" role="math"><math> <mo>-</mo> <mn>2</mn> <mi>a</mi> <mo>-</mo> <mi>b</mi> </math></span>, <span aria-label="b" role="math"><math> <mi>b</mi> </math></span>, <span aria-label="dwa a" role="math"><math> <mn>2</mn> <mi>a</mi> </math></span>, <span aria-label="zero" role="math"><math> <mn>0</mn> </math></span>
Przeciągnij i upuść.
, , ,
a) ............
b) ............
c) ............
d) ............
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15. , 16.
Wybierz.
, , , , , , , , , , , , , , ,
a) ..............
b) ..............
c) ..............
d) ..............
{}
{}
Podaj przykład dwóch wyrażeń algebraicznych, których suma jest równa
Podaj przykład dwóch wyrażeń algebraicznych, których różnica jest równa
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
Dane są wyrażenia algebraiczne.
Wstaw nawiasy w wyrażeniach, tak aby była prawdziwa równość:
Podaj przykład takich sum algebraicznych i , aby prawdziwa była równość
i
i
i
Uzasadnij, że wartość liczbowa wyrażenia
dla każdej liczby ujemnej jest liczbą dodatnią.
Słownik
sumą algebraiczną nazywamy sumę jednomianów.
wyrażenie będące iloczynem liczb i liter (może być też sama liczba lub sama litera).
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.