Stosowanie wyrażeń algebraicznych
6. Mnożenie sum algebraicznych
Strażnikiem wrót prowadzących do pewnej piramidy jest sfinks. Jeśli chcesz wejść do piramidy, musisz rozwiązać zagadkę, którą zada ci sfinks. W przeciwnym razie może zamienić cię w kamień.
Zagadka sfinksa.
Suma dwóch liczb jest równa siedem, a ich różnica jest równa trzynaście. Ile jest równa różnica kwadratów tych liczb?
Czy potrafisz rozwiązać zagadkę sfinksa?
Jeśli nie – zapoznaj się z poniższym materiałem, a znajdziesz tam odpowiedź. Jeśli zagadka została przez Ciebie rozwiązana – również zajrzyj do poniższego materiału, aby rozszerzyć swoje umiejętności.
Bowiem w tym materiale zajmiemy się mnożeniem dwumianów, czy wyrażeń algebraicznych, będących sumą dwóch jednomianów.
Do zrozumienia tematu będzie ci potrzebna wiedza dotycząca jednomianów. Jeśli potrzebujesz dodatkowych informacji na temat działań na jednomianach zajrzyj do materiału Mnożenie i dzielenie sumy algebraicznej przez jednomian.
Prostokąt przedstawiony na rysunku podzielono na mniejsze prostokąty.
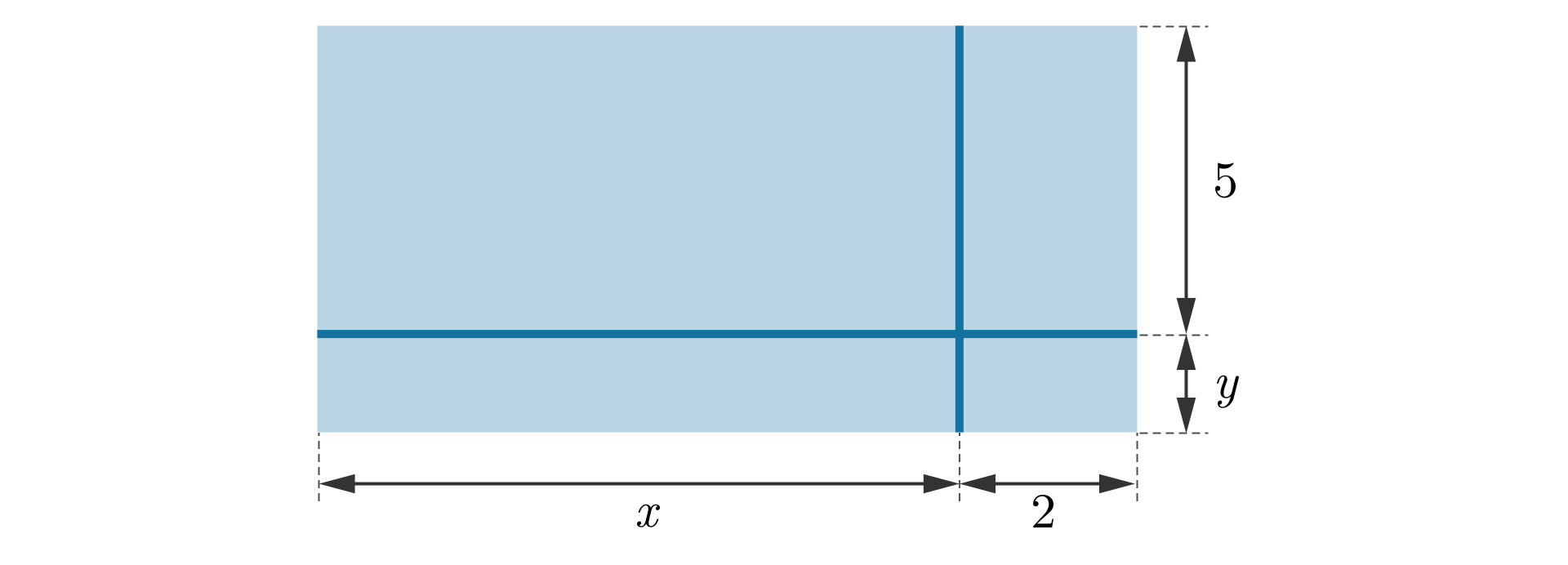
Pole tego prostokąta opisują wyrażenia oraz .
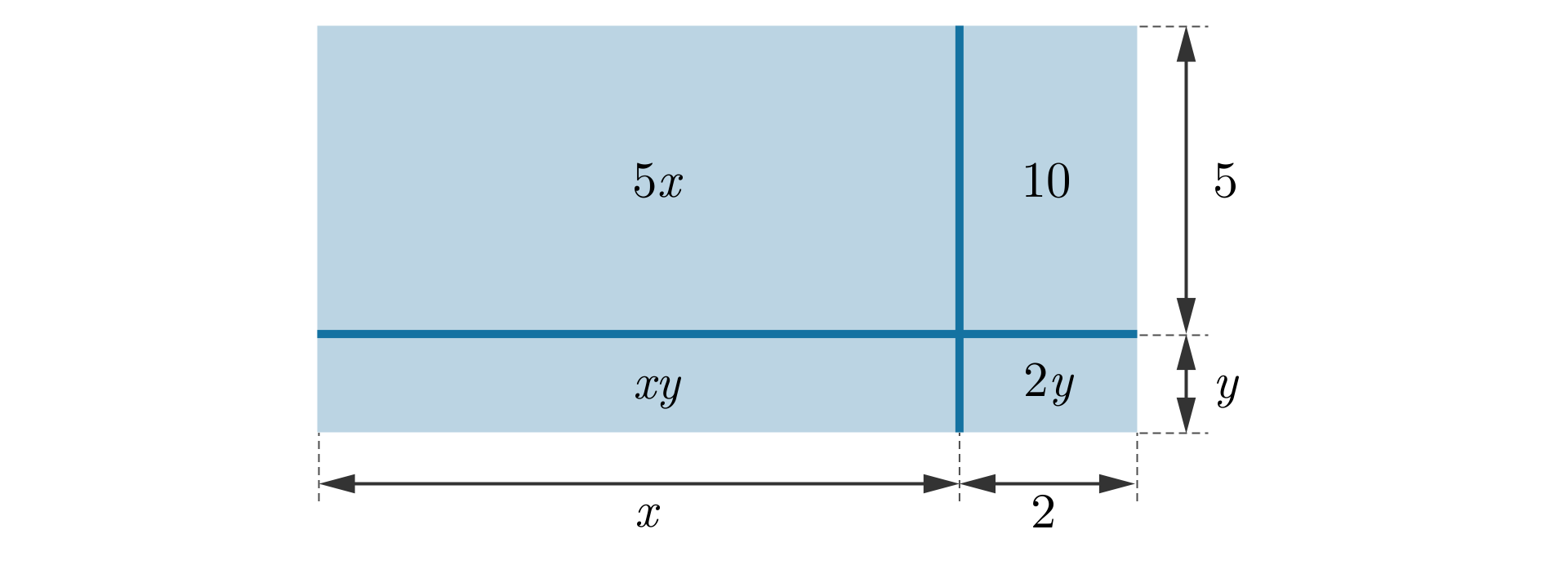
Możemy więc zapisać:
Zatem wyrażenie zapisane po prawej stronie równości otrzymujmy, mnożąc sumy algebraicznemnożąc sumy algebraiczne i .
Chcąc w inny sposób wykonać to mnożenie, stosujemy prawo rozdzielności mnożenia względem dodawania.
Wykonać mnożenie możemy też w prostszej wersji – mnożąc od razu każdy wyraz pierwszego dwumianu, przez każdy wyraz drugiego dwumianu.
Korzystając z powyższego przykładu, podamy sposób mnożenia sum algebraicznychmnożenia sum algebraicznych.
Aby pomnożyć dwie sumy algebraiczne, należy każdy wyraz pierwszej sumy pomnożyć przez każdy wyraz drugiej sumy i otrzymane jednomiany dodać.
Zapiszemy iloczyn w postaci sumy.
Mnożenie | Obliczenia pomocnicze |
|---|---|
Mnożenie sum algebraicznych wykorzystamy do zapisania kwadratu dwumianu w postaci sumy.
Zapiszemy wyrażenie w postaci sumy.
Aby wykonać potęgowanie, zapisujemy kwadrat danego wyrażenia w postaci iloczynu, a następnie mnożymy.
Redukujemy wyrazy podobne.
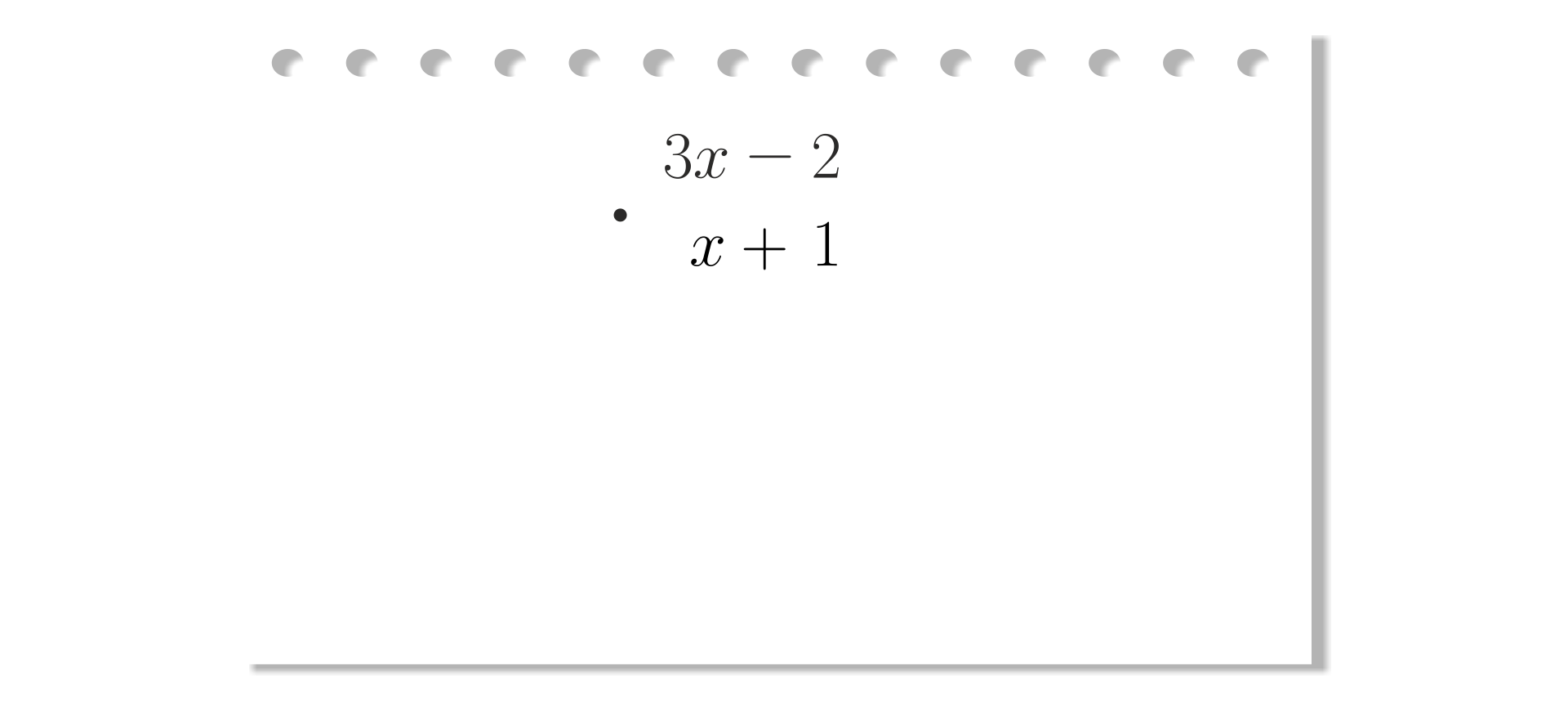
Mnożenie dwumianów czasem wykonujemy sposobem pisemnym, podobnie jak mnożymy liczby naturalne.
Pomnożymy pisemnie i .
Krok
Zapisujemy jeden dwumian pod drugim.
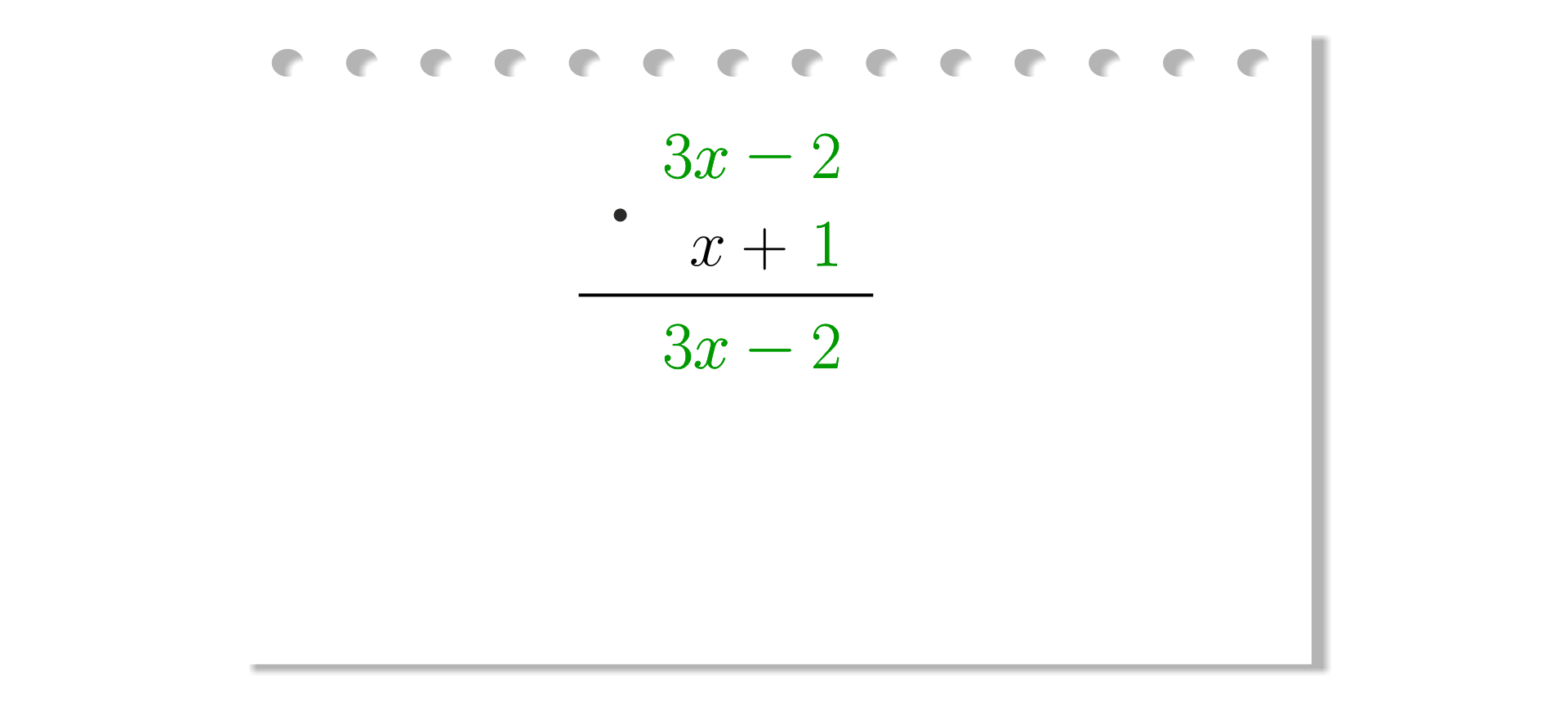
Krok
Mnożymy pierwszy dwumian przez .
Krok
Mnożymy pierwszy dwumian przez .
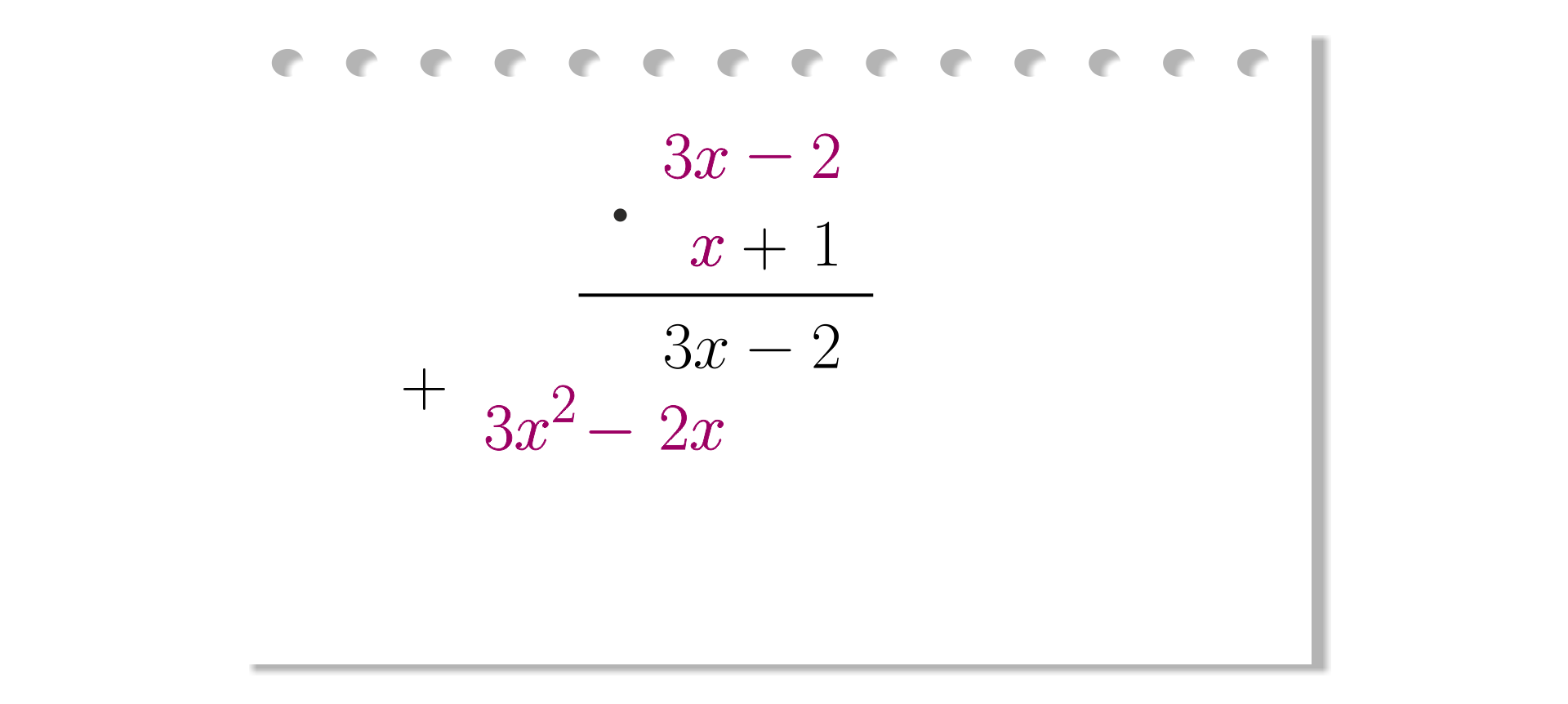
Krok
Dodajemy otrzymane wyrażenia i redukujemy wyrazy podobne.
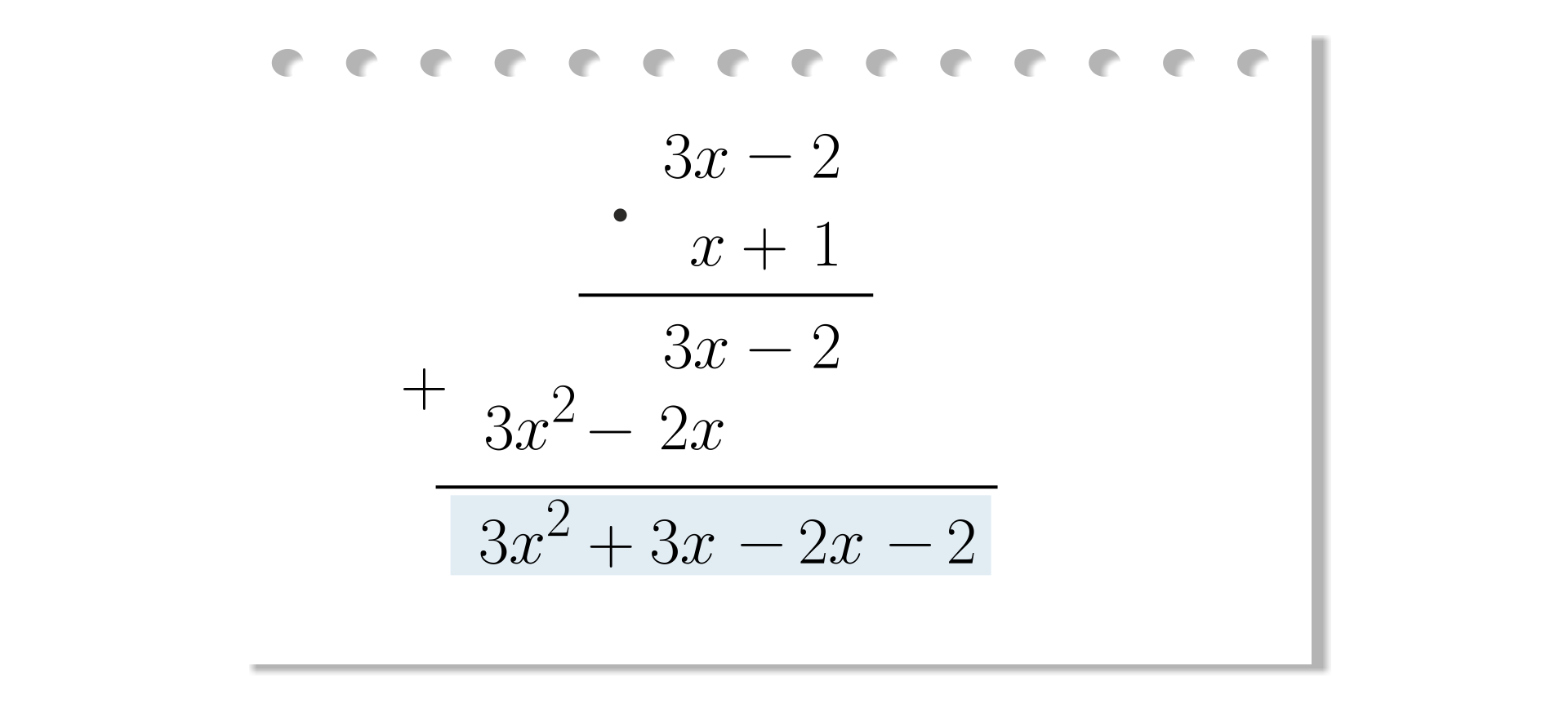
Pomnożymy przez siebie sumy algebraiczne:
.
Pomnożymy przez siebie sumy algebraiczne, wykorzystując prawa działań na potęgach o wykładniku naturalnym.
.
Poznane sposoby mnożenia można zastosować do mnożenia wyrażeń zawierających pierwiastki.
Zapiszemy w prostszej postaci wyrażenie .
Zauważmy, że: i .
Redukujemy wyrazy podobne.
Podstawą prostopadłościanu jest prostokąt o bokach długości i , gdzie . Wysokość tego prostopadłościanu jest równa . Zapiszemy wzór, który pozwoli na obliczenie objętości tego prostopadłościanu.
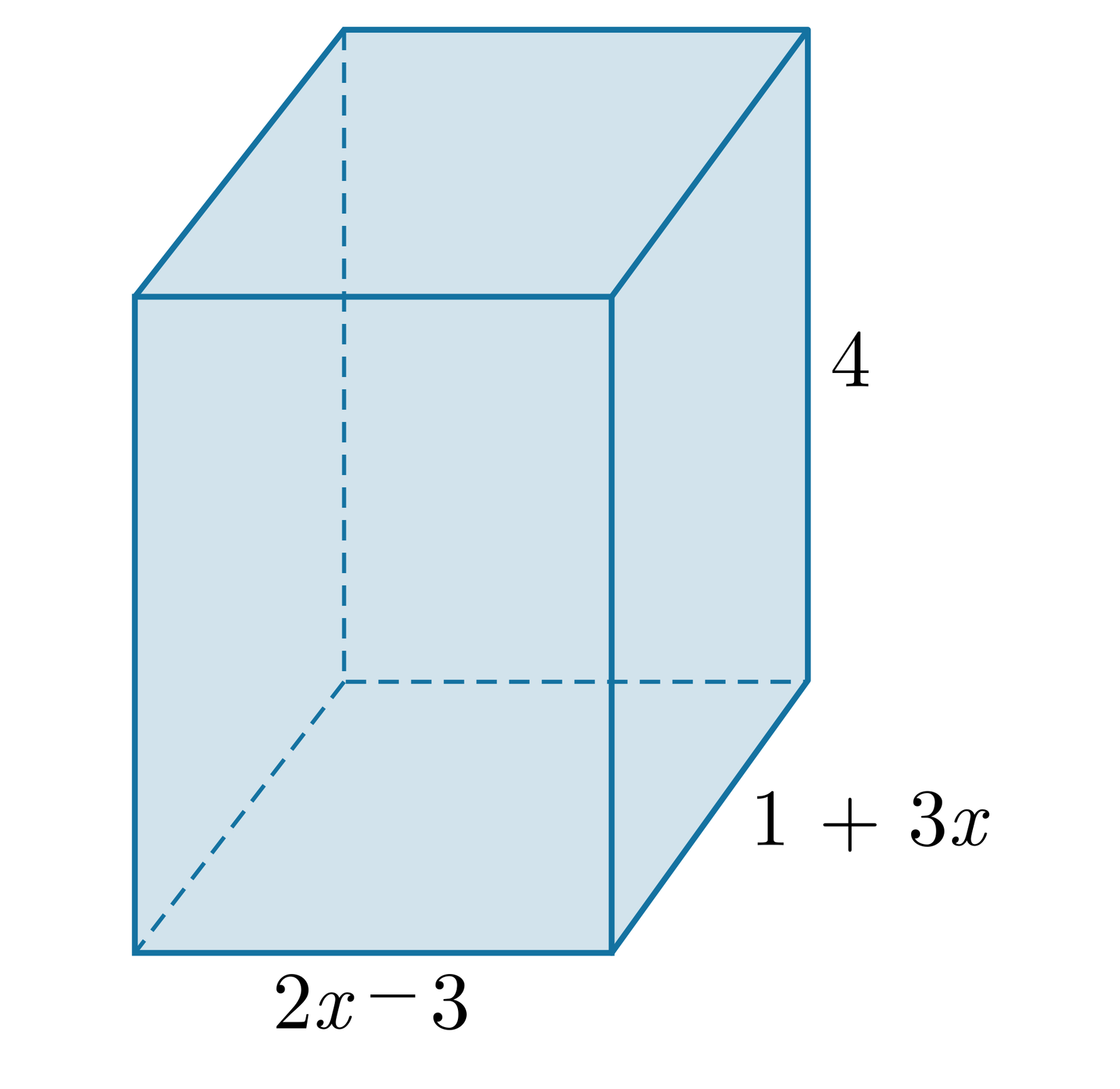
Aby obliczyć objętość prostopadłościanu, mnożymy wysokość prostopadłościanu przez pole podstawy tego prostopadłościanu.
W tym przypadku mnożymy najpierw pierwszą sumę przez , a następnie tak otrzymane wyrażenie mnożymy przez .
Aby pomnożyć przez siebie dwie sumy algebraiczne, mnożymy każdy wyraz pierwszej sumy przez każdy wyraz drugiej sumy.
Pomnożymy przez siebie trzy sumy algebraiczne
W pierwszej kolejności mnożymy przez siebie dwie sumy algebraiczne, a następnie wynik tego działania mnożymy przez trzecią sumę.
.
Ilustracja interaktywna
Obejrzyj materiał ilustrujący różne sposoby zamiany iloczynu dwumianów na sumę.
Zapoznaj się z materiałem opisującym sposoby zamiany iloczynu dwumianów na sumę. Różne sposoby mnożenia dwumianów i .
Sposób pierwszy:
Korzystamy z rozdzielności mnożenia względem dodawania.
,
,
,
.
Drugi sposób:
Korzystamy z interpretacji graficznej.
Kolumna pierwsza | Kolumna druga | Kolumna trzecia |
|---|---|---|
Kolumna pierwsza | Kolumna druga | Kolumna trzecia |
|---|---|---|
,
.
Trzeci sposób:
Pomnożymy dwumiany pisemnie.
Mnożenie sposobem pisemnym: oraz .
Pod kreską zapisano:.
Pod spodem z jednym przesunięciem w lewą stronę zapisano:.
Pod kreską zapisano wynik:
,
.
Zapisz w najprostszej postaci wyrażenie , gdy i .
Skorzystaj z rozdzielności mnożenia względem dodawania.
Wykonaj mnożenie: .
Skorzystaj z interpretacji graficznej mnożenia.
Zapisz w najprostszej postaci wyrażenie
Zaznacz prawidłowe dokończenie zdania. Wyrażenie algebraiczne opisujące pole prostokąta przedstawionego na rysunku to:
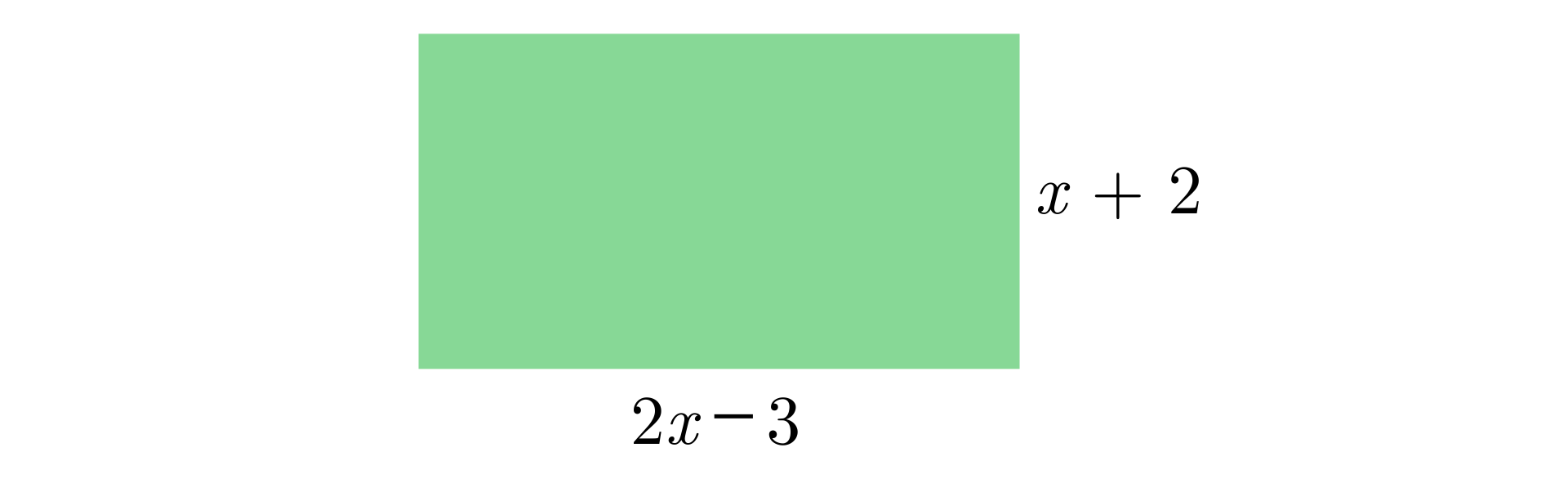
Tu uzupełnij
Tu uzupełnij
Tu uzupełnij
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
1. , 2. , 3. , 4.
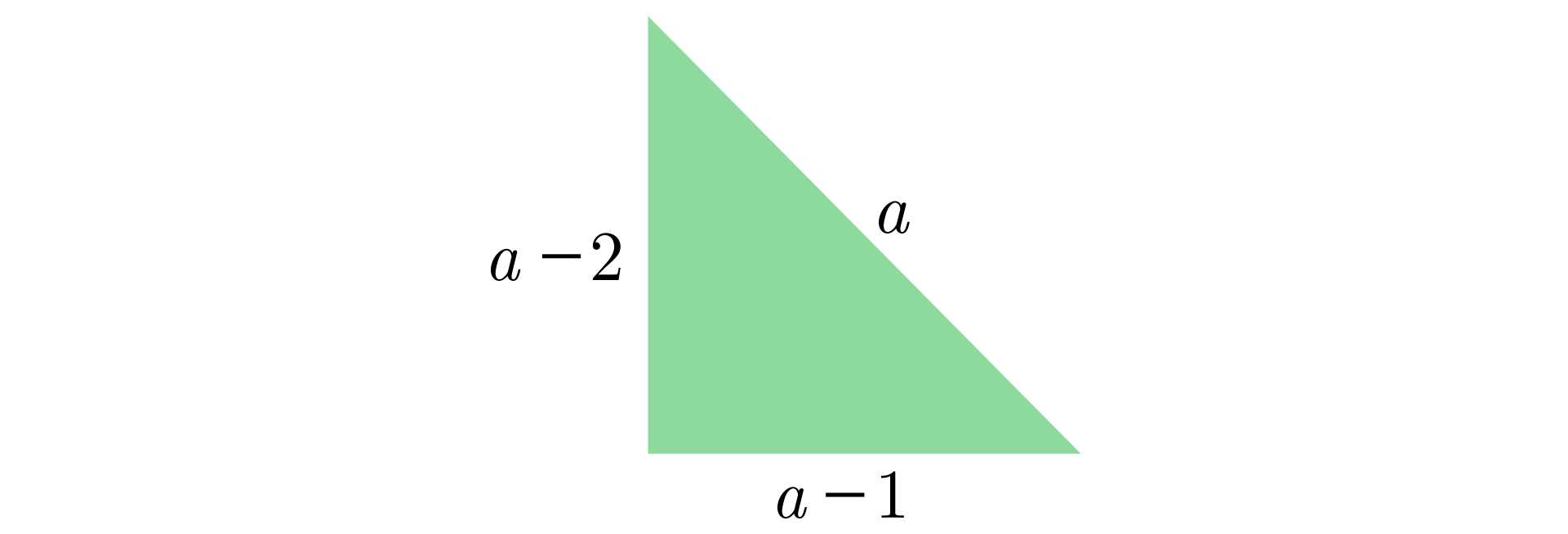
Uzasadnij, że liczba jest liczbą całkowitą.
Zapisz podane wyrażenie w postaci sumy i zredukuj wyrazy podobne.
Pomnóż sumy algebraiczne.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12. , 13. , 14. , 15.
Połącz w pary.
<span aria-label=" minus, sześć x indeks górny, dwa, y, plus, dwanaście x indeks górny, dwa, plus, piętnaście x y indeks górny, dwa, minus, trzydzieści x y" role="math"><math><mo>-</mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mi>y</mi><mo>+</mo><mn>12</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>15</mn><mi>x</mi><msup><mi>y</mi><mn>2</mn></msup><mo>-</mo><mn>30</mn><mi>x</mi><mi>y</mi></math></span>, <span aria-label=" minus, dwanaście x indeks górny, dwa, y indeks górny, trzy, plus, sześć x y indeks górny, trzy, plus, szesnaście x indeks górny, dwa, y, minus, osiem x y" role="math"><math><mo>-</mo><mn>12</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>3</mn></msup><mo>+</mo><mn>6</mn><mi>x</mi><msup><mi>y</mi><mn>3</mn></msup><mo>+</mo><mn>16</mn><msup><mi>x</mi><mn>2</mn></msup><mi>y</mi><mo>-</mo><mn>8</mn><mi>x</mi><mi>y</mi></math></span>, <span aria-label=" minus, pięć x indeks górny, dwa, y indeks górny, dwa, plus, dwadzieścia x indeks górny, trzy, y indeks górny, dwa, plus, osiem x y indeks górny, trzy, minus, trzydzieści dwa x indeks górny, dwa, y indeks górny, trzy" role="math"><math><mo>-</mo><mn>5</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><mn>20</mn><msup><mi>x</mi><mn>3</mn></msup><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><mn>8</mn><mi>x</mi><msup><mi>y</mi><mn>3</mn></msup><mo>-</mo><mn>32</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>3</mn></msup></math></span>, <span aria-label=" minus, jedenaście x indeks górny, dwa, y indeks górny, dwa, plus, dwanaście x indeks górny, trzy, y, plus, dwa przecinek pięć x y indeks górny, trzy" role="math"><math><mo>-</mo><mn>11</mn><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><mo>+</mo><mn>12</mn><msup><mi>x</mi><mn>3</mn></msup><mi>y</mi><mo>+</mo><mn>2</mn><mo>,</mo><mn>5</mn><mi>x</mi><msup><mi>y</mi><mn>3</mn></msup></math></span>, <span aria-label=" minus, sześć x indeks górny, dwa, plus, dwadzieścia dwa x y, minus, dwanaście y indeks górny, dwa" role="math"><math><mo>-</mo><mn>6</mn><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>22</mn><mi>x</mi><mi>y</mi><mo>-</mo><mn>12</mn><msup><mi>y</mi><mn>2</mn></msup></math></span>
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11.
Przeciągnij i upuść jednomiany tak, aby podane równości były prawdziwe.
, , , , , , ,
a) ................
b) ................
c) ................
d) ................ ................
e) ................
f) ................
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. , 11. , 12.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Przeciągnij i upuść jednomiany tak, aby podane równości były prawdziwe.
, , , , , ,
a) ............
b) ............
c) ............
d) ............
Zapisz w postaci wyrażenia algebraicznego pole poniższego trapezu.

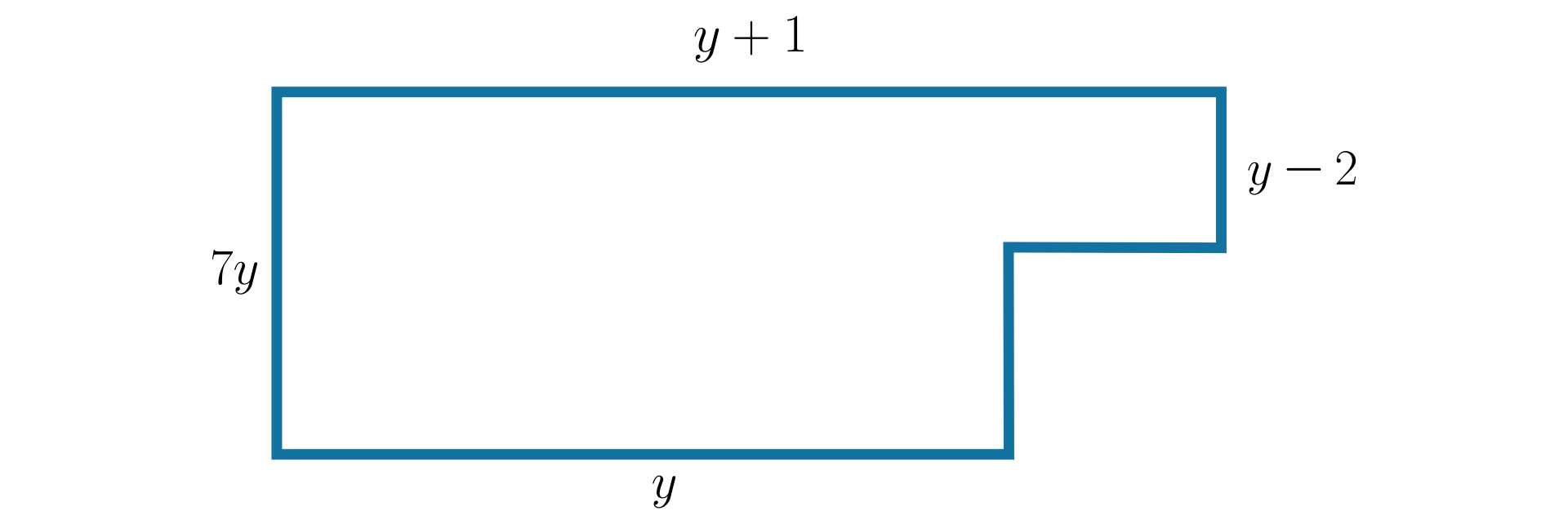
Jakie wyrażenie algebraiczne opisuje pole wielokąta przedstawionego na rysunku poniżej?
Prostokątny obraz umieszczono w ramie. Obraz wraz z ramą ma długość i szerokość . Jakie jest pole powierzchni obrazu, jeżeli szerokość ramy wynosi ?
Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź.

, i . Jaką objętość będzie miał prostopadłościan, którego każda z krawędzi ma długość o większą? Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź. Odpowiedź: Objętość prostopadłościanu wynosi 1. , 2. , 3. , 4. .
Iloczyn dwóch kolejnych liczb nieparzystych, z których mniejsza jest równa to 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Iloczyn trzech kolejnych liczb parzystych, z których najmniejsza jest równa to 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
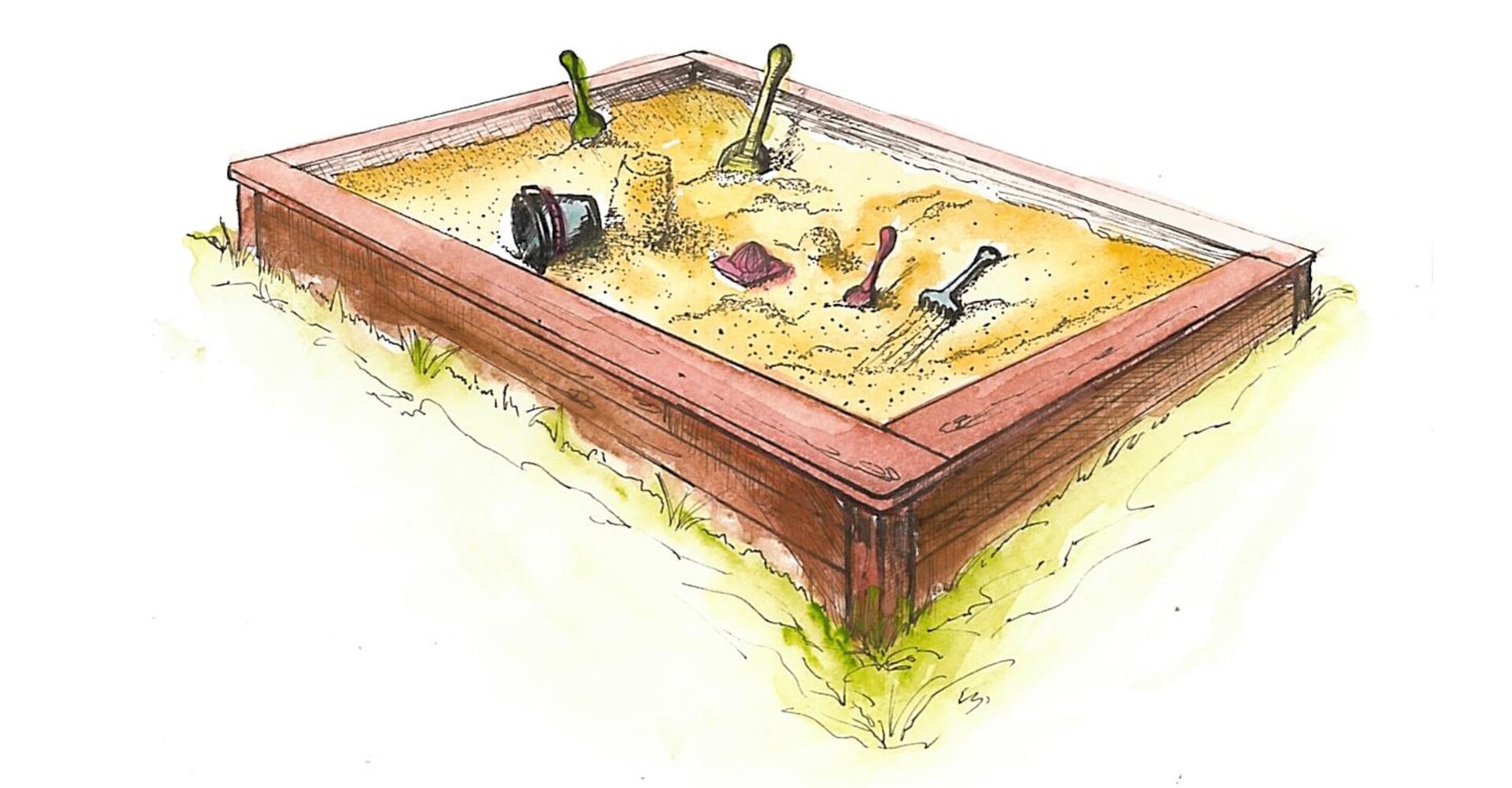
Piaskownica jest prostokątem o długości metrów centymetrów i szerokości metrów centymetrów. Ile metrów kwadratowych ma pole powierzchni piaskownicy? Uzupełnij poniższe zdanie odpowiednim wyrażeniem algebraicznym. Kliknij w lukę aby rozwinąć listę i wybierz prawidłową odpowiedź.
Słownik
Aby pomnożyć dwie sumy algebraiczne, należy każdy wyraz pierwszej sumy pomnożyć przez każdy wyraz drugiej sumy i otrzymane jednomiany dodać.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.