Przykłady wyrażeń algebraicznych.
$a+7$ – suma liczb $a$ i $7$
$x-2y$ – różnica liczb $x$ i $2y$
$5·\left(6-x\right)$ – iloczyn liczby $5$ i różnicy liczby $6$ i liczby $x$
$\frac{x}{2y}$ – iloraz liczby $x$ przez podwojoną liczbę $y$

Zapiszemy w najprostszej postaci wyrażenie $W={\left(3x\right)}^2-\left(3x-1\right)\left(3x+2\right)$ i obliczymy jego wartość dla $x=-1$.

Aby obliczyć wartość liczbową tego wyrażenia, podstawiamy w miejsce $x$ liczbę $\left(-1\right)$.

Odpowiedź:
Wartość liczbowa wyrażenia dla $x=-1$ jest równa $5$.

Zapiszemy za pomocą wyrażenia algebraicznegowyrażenie algebraicznewyrażenia algebraicznego liczbę naturalną dwucyfrową podzielną przez $5$, której cyfrą dziesiątek jest $a$, natomiast cyfrą jedności jest $b$.

Liczbę dwucyfrową, której cyfrą dziesiątek jest $a$, natomiast cyfrą jedności jest $b$, można zapisać w dziesiątkowym układzie pozycyjnym w postaci:
$10a+b$.
Aby liczba była podzielna przez $5$, jej cyfrą jedności musi być $0$ lub $5$.
Aby liczba była dwucyfrowa, jej cyfra dziesiątek nie może być równa $0$.

Zatem liczba spełniająca warunki zadania to $10a+b$, dla $b=0$ lub $b=5$ i $a\in \left\{1, 2, 3, 4, 5, 6, 7, 8, 9\right\}$.

Wykażemy, że jeżeli od odwrotności liczby naturalnej $n$ odejmiemy odwrotność liczby o $1$ większej od $n$, to otrzymamy ułamek właściwy.

Odwrotnością liczby $n$ jest liczba $\frac{1}{n}$.
Odwrotnością liczby o $1$ większej od $n$, czyli liczby $n+1$ jest liczba $\frac{1}{n+1}$.
Aby wyrażenia $\frac{1}{n}$ i $\frac{1}{n+1}$ miały sens liczbowy, mianowniki ułamków muszą być różne od zera.
Czyli musi być spełniony warunek
$n\ne 0$ i $n+1\ne 0$, czyli $n\ne -1$.
Ponieważ $n$ jest liczbą naturalną, zatem powyższy warunek będzie spełniony, gdy $n$ będzie liczbą naturalną różną od zera.

Zapisujemy i przekształcamy różnicę wynikającą z treści zadania.
Sprowadzamy ułamki do wspólnego mianownika (tak, jak byśmy to robili w przypadku ułamków zwykłych – czyli rozszerzamy odpowiednio ułamki) i odejmujemy.

Iloczyn $n\left(n+1\right)$ jako iloczyn dwóch liczb naturalnych jest liczbą naturalną. Ponieważ $n\ne 0$, więc liczba $n\left(n+1\right)$ jest większa bądź równa $2$.
$2>1$ – czyli mianownik ułamka $\frac{1}{n\left(n+1\right)}$ jest większy od licznika, a to oznacza, że jest to ułamek właściwy.

Podstawą prostopadłościanu jest prostokąt o bokach długości $a$ i $0,75a$. Długość krawędzi bocznej jest równa $2a$. Obliczymy objętość tego prostopadłościanu.

Sporządzamy rysunek pomocniczy.

R1cIpzxacxk9N

Ilustracja przedstawia prostopadłościan, którego kolejne wymiary wynoszą $a$, $0,75a$ oraz $2a$.

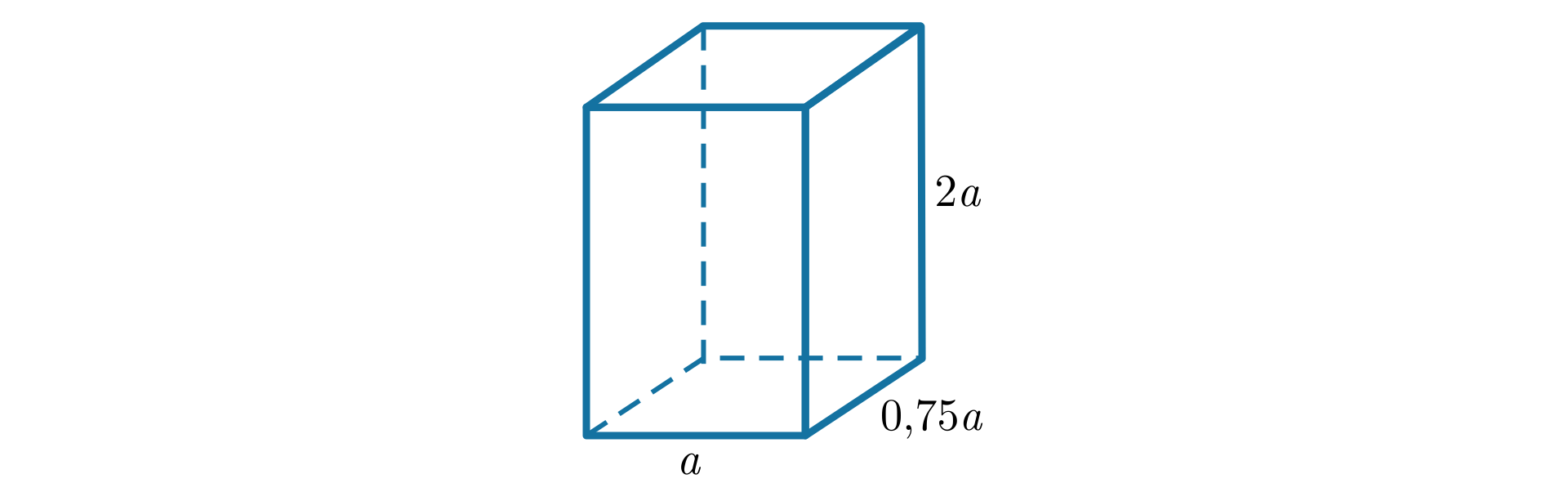
Aby obliczyć objętość prostopadłościanu, należy pomnożyć pole podstawy prostopadłościanu przez wysokość.

Zauważmy przy tym, że $a>0$.

Odpowiedź:
Objętość prostopadłościanu jest równa $1,5a^3$.

Czworokąt na rysunku to kwadrat. Obliczymy pole zamalowanej figury dla $a=4$.

R1FD7v5TfGkPd

Rysunek przedstawia kwadrat o boku długości a. Poprowadzona jest linia z lewego dolnego rogu kwadratu do środka przeciwległego boku. Linia ta dzieli kwadrat na biały trójkąt prostokątny z wcześniej opisaną linią, jako przeciwprostokątną oraz przyprostokątnymi długości a i jedna druga a oraz trapez prostokątny. Trapez jest pomalowany na zielono.

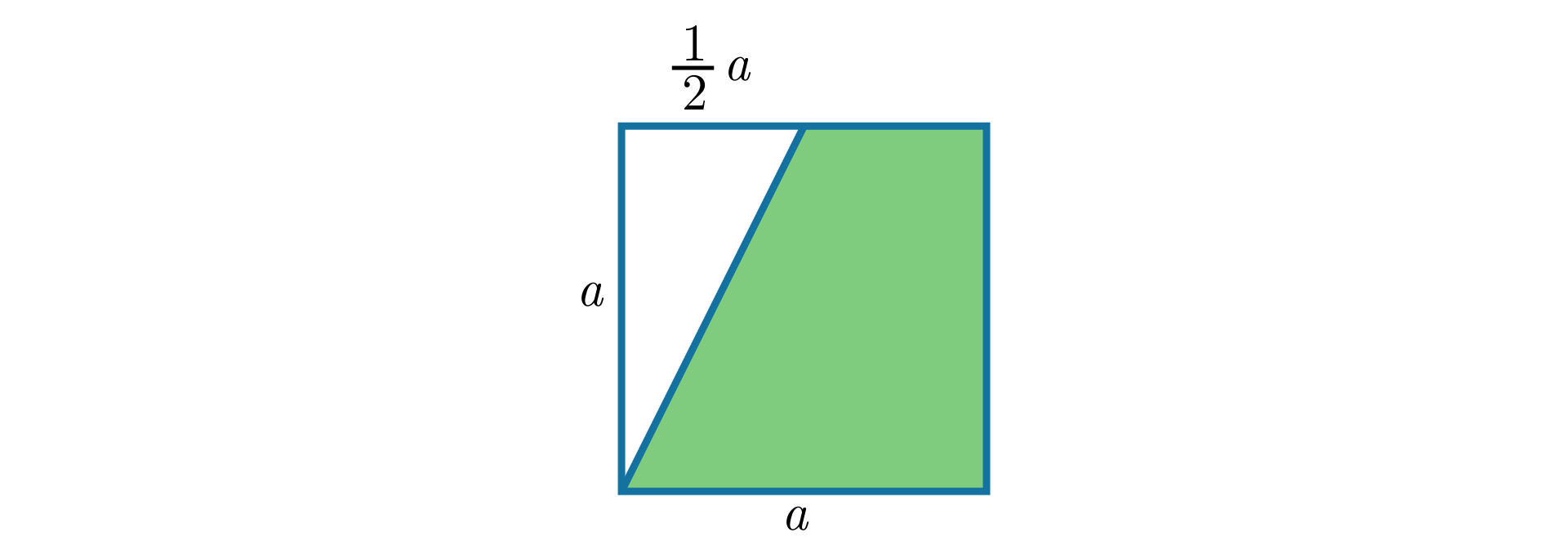
Pole zamalowanej figury obliczamy jako różnicę pola kwadratu o boku długości $a$ i pola trójkąta prostokątnego o przyprostokątnych długości $a$ i $\frac{1}{2}a$.

Obliczamy teraz pole zamalowanej figury dla $a=4$. W miejsce $a$ podstawiamy do otrzymanego wyrażenia liczbę $4$.

Odpowiedź:
Dla $a=4$ pole zamalowanej figury jest równe $12$.

W trójkącie miary kątów pozostają w stosunku $1:2:3$. Wykażemy, że ten trójkąt jest prostokątny.

Oznaczmy:
$a$ – miara najmniejszego z kątów.

Wtedy pozostałe kąty tego trójkąta mają miary: $2a$ i $3a$.
Suma miar kątów trójkąta jest równa $180°$, czyli:

Miary pozostałych kątów:

Jeden z kątów trójkąta ma miarę $90°$, więc trójkąt jest prostokątny, co należało wykazać.

Obliczymy resztę z dzielenia przez $9$ różnicy dowolnej liczby trzycyfrowej $A$ i liczby trzycyfrowej $B$ powstałej z liczby $A$ w wyniku przestawienia cyfry setek i cyfry dziesiątek.

Oznaczmy przez $a$, $b$, $c$ cyfry liczby $A$, gdzie $a\ne 0$ i $b\ne 0$.

Wtedy:

oraz

Wyznaczamy różnicę tych liczb.

Różnicę liczb $A$ i $B$ zapisaliśmy w postaci iloczynu liczby $9$ i liczby całkowitej $10a-10b$, co oznacza, że jest to liczba podzielna przez $9$.

Odpowiedź:
Reszta z dzielenia liczby $A-B$ przez $9$ jest równa $0$.

W bombonierce było $c$ czekoladek. Patryk, Wojtek i Bartek podzielili między siebie czekoladki. Patryk wziął dwie czekoladki i połowę reszty. Wojtek wziął połowę tego, co zostało. Bartkowi przypadła reszta czekoladek. Ile czekoladek otrzymał Bartek?

Wykonujemy rysunek pomocniczy.

RPBocWvKzx7eP

Ilustracja przedstawia oś z czternastoma podziałkami. Pierwsze dwie zamalowane są kolorem fioletowym, kolejne sześć podziałek kolorem zielonym, kolejne trzy kolorem żółtym i trzy ostatnie kolorem różowym. Nad podziałkami w kolorze fioletowym i zielonym napisano Patryk, nad żółtymi podziałkami zapisano Wojtek, a nad różowymi Bartek. Pod fioletowymi podziałkami zapisano dwa, pod zielonymi $\frac{c-2}{2}$, pod żółtymi i różowymi $\frac{c-2}{4}$.

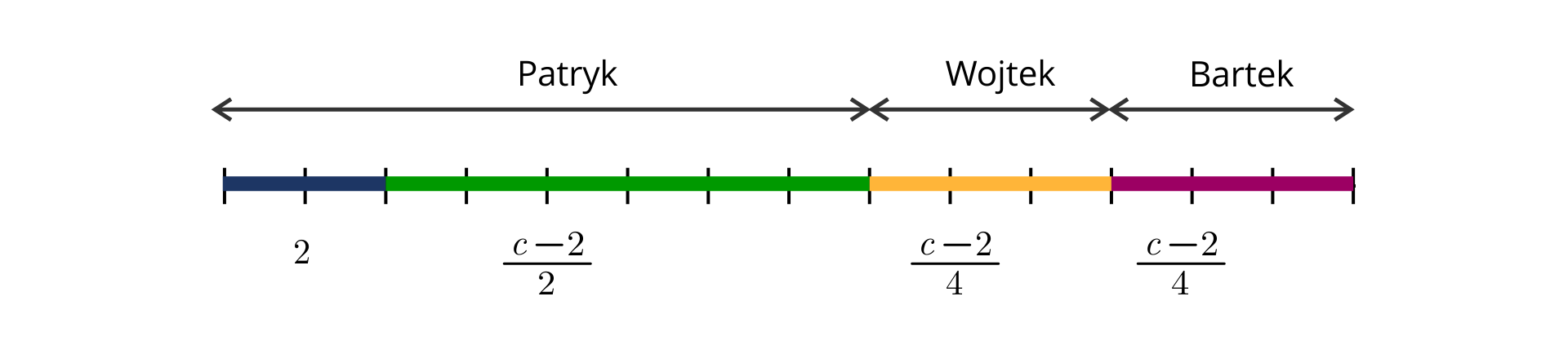
• Patryk najpierw wziął dwie czekoladki – zostało $c-2$ czekoladek. Potem wziął jeszcze połowę reszty, czyli $\frac{c-2}{2}$. Zostało $\frac{c-2}{2}$ czekoladek.

• Wojtek wziął połowę tego, co zostało, czyli $\frac{1}{2}·\frac{c-2}{2}=\frac{c-2}{4}$ czekoladek.

• Obliczamy, ile czekoladek zostało dla Bartka. Zapisujemy i przekształcamy odpowiednie wyrażenie.

Zauważmy, że takie rozwiązanie mogliśmy też odczytać z rysunku.

Odpowiedź:
Bartek otrzymał $\frac{c-2}{4}$ czekoladki.

Agata ma $4$ lata, a Wanda $10$. Ustalimy, za ile lat Wanda będzie dwa razy starsza od Agaty.

$\mathrm{I}$ sposób:

Sporządzamy pomocniczą tabelkę.

Z danych tabeli otrzymujemy równość

Zatem

Odpowiedź:
Za dwa lata Wanda będzie dwukrotnie starsza od Agaty.

$\mathrm{II}$ sposób:

W rozwiązaniu może pomóc nam też rysunek.

R1NulV44K1xks

Ilustracja przedstawia trzy osie z podziałkami podpisanymi od zera do piętnastu. Każda oś znajduje się jedna pod drugą. Pierwsza z nich podpisana jest Obecnie. Zaznaczono na osi kolorem żółtym odcinek od zera do czterech i podpisano Agata, a kolorem zielonym odcinek od zera do dziesięciu i podpisano Wanda. Druga z nich podpisana jest Za rok. Zaznaczono na osi kolorem żółtym odcinek od zera do pięciu i podpisano Agata, a kolorem zielonym odcinek od zera do jedenastu i podpisano Wanda. Trzecia z nich podpisana jest Za dwa lata. Zaznaczono na osi kolorem żółtym odcinek od zera do sześciu i podpisano Agata, a kolorem zielonym odcinek od zera do dwunastu i podpisano Wanda.

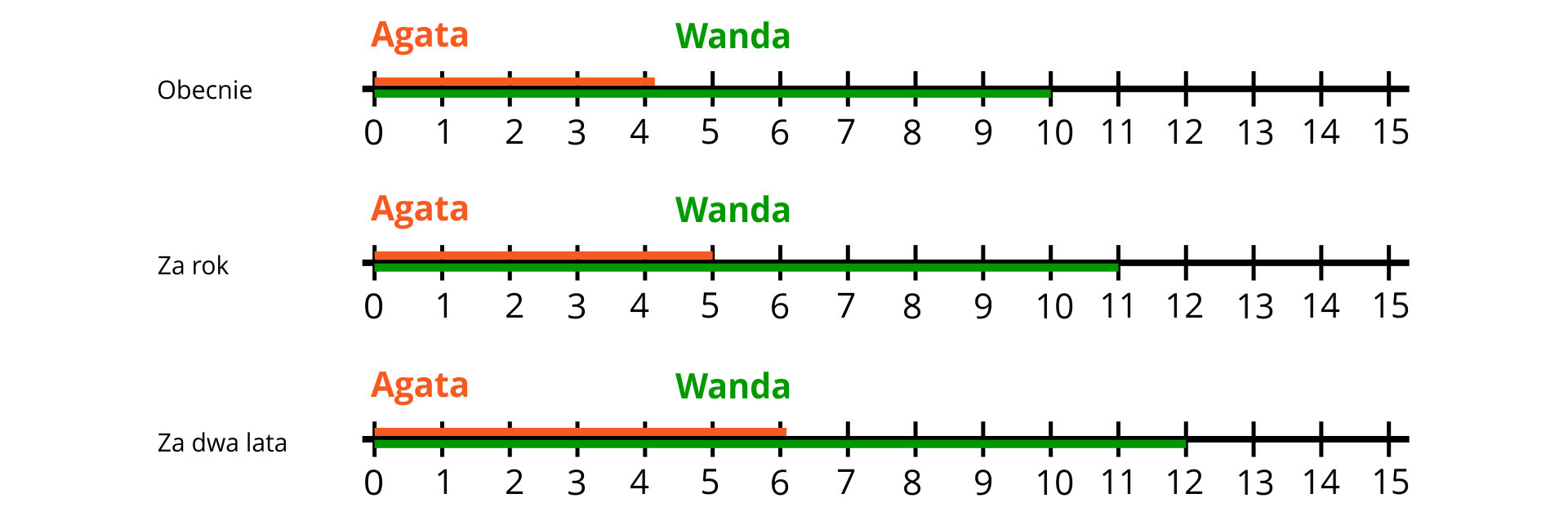
Na podstawie rysunku wnioskujemy, że Wanda będzie dwa razy starsza od Agaty za dwa lata.
Istotnie – za dwa lata Agata będzie miała $4+2=6$ lat, a Wanda $10+2=12$ lat.

Odpowiedź:
Za dwa lata Wanda będzie dwukrotnie starsza od Agaty.

nazywamy wyrażenie zbudowane z liczb, liter, znaków działań, nawiasów.