Aplet
Polecenie 1
Zapoznaj się z Apletem. Zobacz jak zmieniają się wartości kątów przy zmianie wielkości graniastosłupa.
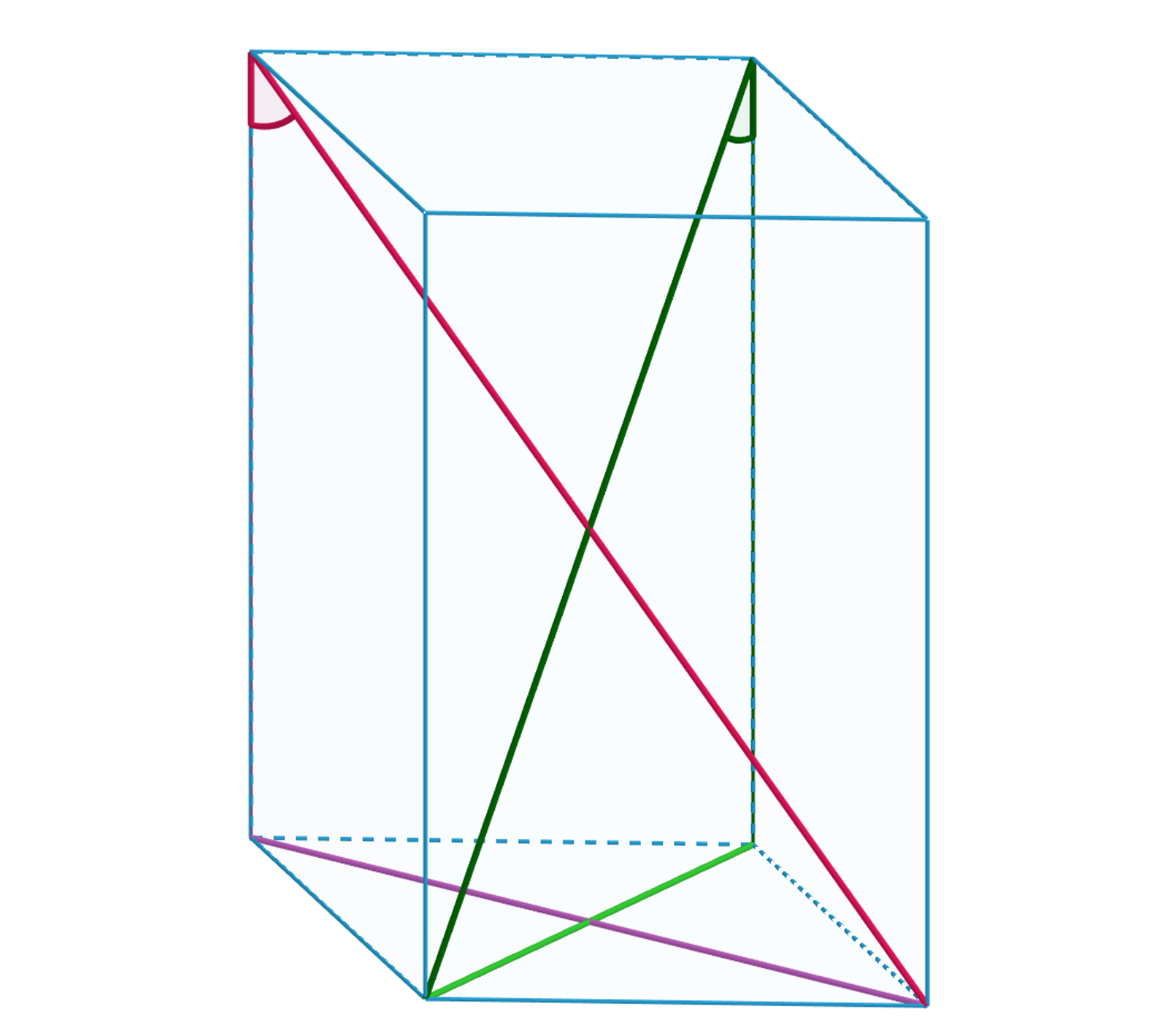
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D11AY2ORf
Polecenie 2
Jaki graniastosłup otrzymamy gdy ? Ile rodzajów kątów między przekątnymi graniastosłupa, a krawędzią boczną otrzymamy?
Polecenie 3
Ustaw wartości i oraz . Spróbuj samodzielnie obliczyć miary kątów przedstawionych w aplecie. Sprawdź wyniki z Apletem.
Jaką miarę ma wtedy kąt pomiędzy przekątną ściany bocznej, a krawędzią podstawy?