Symulacja interaktywna
Polecenie 1
Korzystając z symulacji interaktywnej przeanalizuj zbiory punktów (wielokąty foremne, wykresy funkcji), które mają środek symetrii. Możesz zmieniać wartości parametrów używając suwaków.
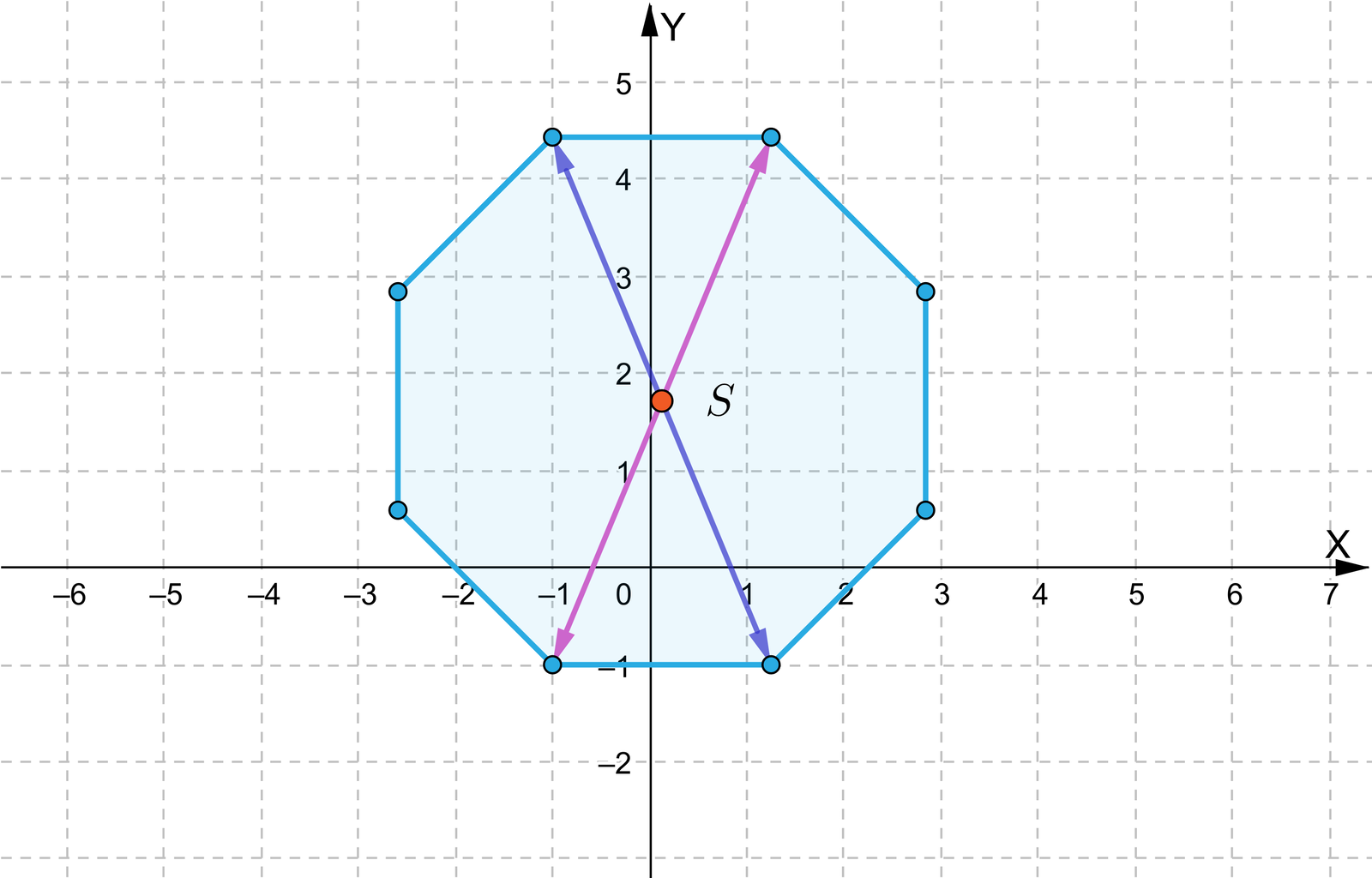
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1G7sfJDA
Polecenie 2
Korzystając z symulacji interaktywnej zaznacz wszystkie zdania prawdziwe.
- Pewien –kąt foremny ma środek symetrii. Liczba nie może być równa .
- Wykres funkcji o wzorze ma środek symetrii w punkcie .
- Wykres funkcji o wzorze ma środek symetrii w punkcie .
- Wykres funkcji o wzorze ma środek symetrii w punkcie .
- Wykres funkcji o wzorze ma środek symetrii w punkcie .