Symulacja interaktywna

Polecenie 1

Uruchom symulację interaktywną. Ustal położenie wierzchołków trójkąta. Odczytaj długości promieni $r$ , $R$ okręgów wpisanego i opisanego na trójkącie oraz odległość $d$ środków tych okręgów. Oblicz wartość wyrażenia $R^{2} - 2 R \cdot r - d^{2}$ . Sformułuj hipotezę dotyczącą wartości tego wyrażenia.

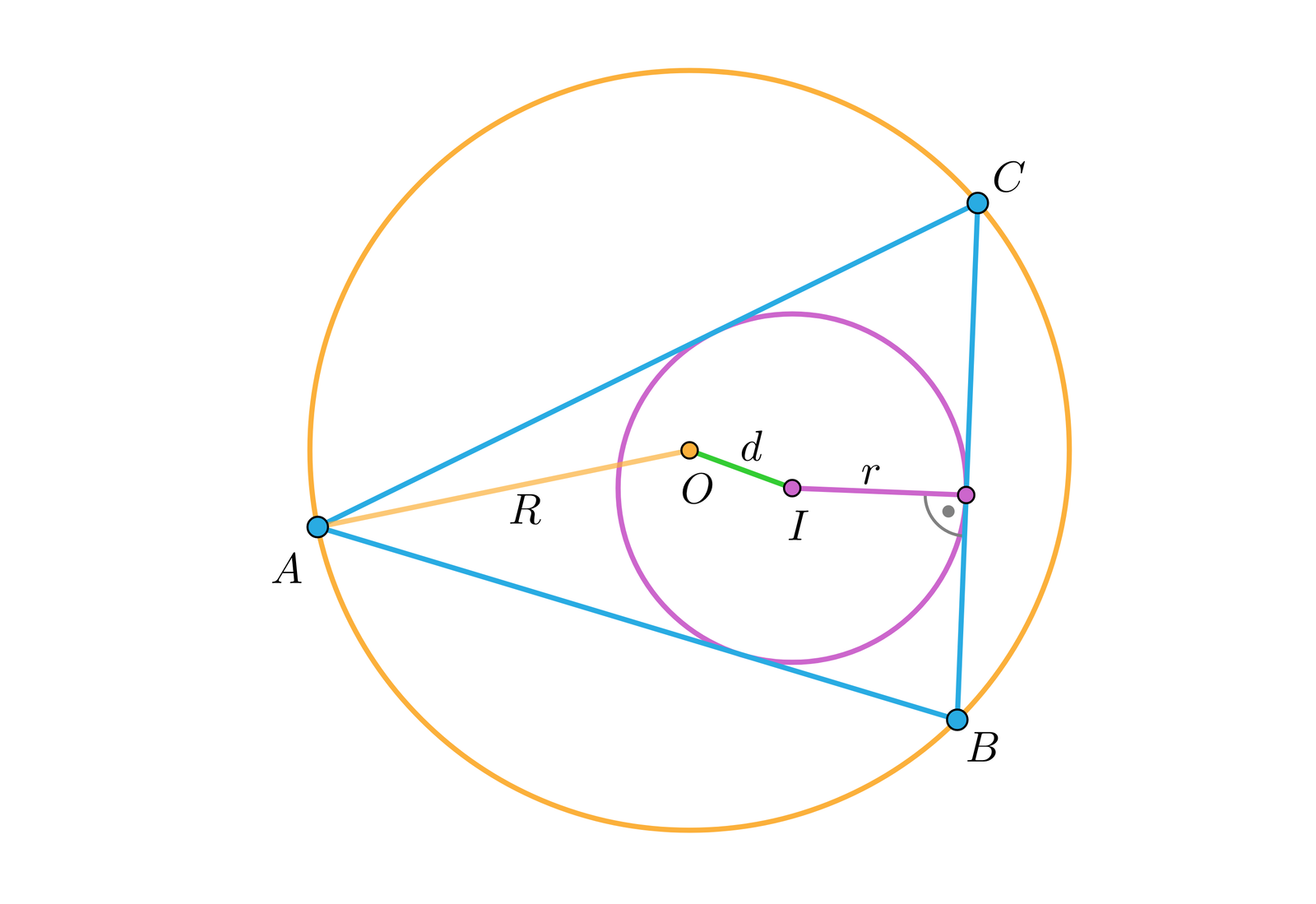
W dowolnym trójkącie $d^{2} = R^{2} - 2 R \cdot r$ , co jest treścią twierdzenia Eulera. Oznacza to, że wyrażenie $R^{2} - 2 R \cdot r - d^{2}$ ma wartość $0$ .

Polecenie 1

Zapoznaj się z poniższym opisem apletu, w którym zaprezentowano różne przypadki okręgów: opisany na trójkącie oraz wpisany w trójkąt. Zwróć uwagę na relację promieni obu takich okręgów.

R1BhCP8TaaVrL

Polecenie 2

Odległość środków okręgów opisanego na trójkącie równoramiennym i wpisanego w dany trójkąt jest równa $4$ . Promień okręgu wpisanego jest równy $3$ . Wyznacz promień okręgu opisanego budując odpowiedni model w Aplecie oraz korzystając z twierdzenia Eulera.

Mamy $d^{2} = R^{2} - 2 R \cdot r$ , czyli $4^{2} = R^{2} - 2 R \cdot 3$ . Prowadzi to do równania kwadratowego $R^{2} - 6 R - 16 = 0$ . Rozwiązaniem tego równania są liczby $8$ , $(- 2)$ . Zatem szukany promień ma długość $8$ .

Polecenie 3

Przeanalizuj położenie wierzchołków $A$ , $B$ , $C$ trójkąta w kontekście wartości ilorazu $\frac{R}{r}$ długości promieni okręgów opisanego i wpisanego w dany trójkąt. Jakie wartości może przyjmować ten iloraz, w szczególności rozstrzygnij, czy może on być mniejszy niż $2$ . Zbadaj, kiedy ten iloraz będzie równy $2$ .

Oczywiście $\frac{R}{r} \in ⟨2, \infty)$ . Równość $\frac{R}{r} = 2$ zachodzi dla trójkąta równobocznego.

Przeczytaj

Sprawdź się