Symulacja interaktywna
Polecenie 1
Uruchom symulację interaktywną. Odczytaj, jakie wartości po przesunięciu paraboli, będącej wykresem funkcji kwadratowej przyjmują współrzędne wierzchołka paraboli oraz równanie osi symetrii. Określ również miejsce zerowe oraz przedziały monotoniczności otrzymanej funkcji.
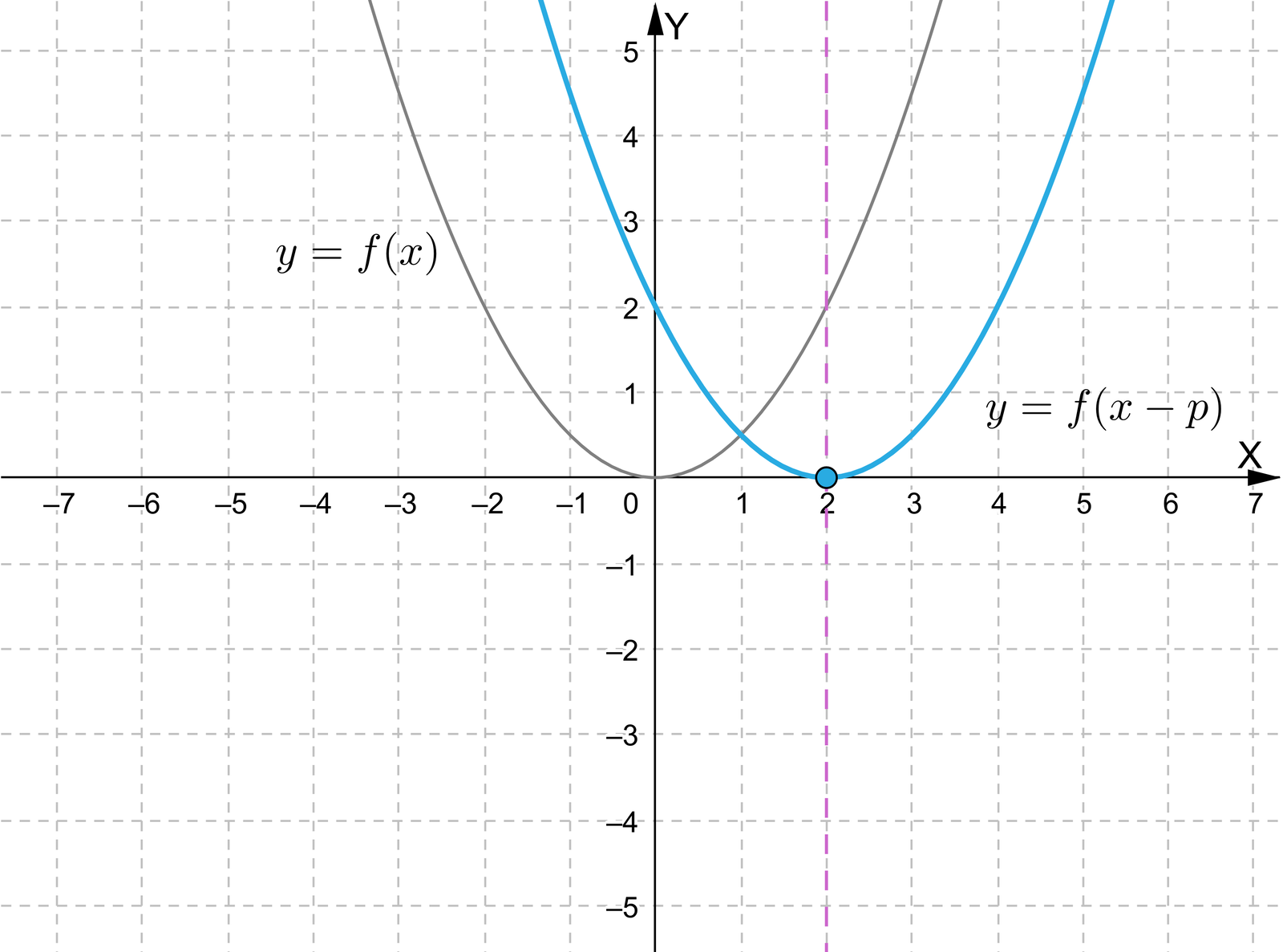
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DFQUAWv3S
Polecenie 2
Dana jest funkcja określona wzorem . Podaj współrzędne wierzchołka paraboli, która jest wykresem tej funkcji, równanie osi symetrii, miejsce zerowe oraz przedziały monotoniczności dla funkcji w przekształceniu, jeżeli po przesunięciu paraboli, będącej wykresem funkcji otrzymujemy parabolę, będącą wykresem funkcji określonej wzorem:
a)
b)