Kąty i ich rodzaje
Wiemy, że niektóre ulice naszych miast mogą leżeć względem siebie prostopadle lub równoległe. A jak opisać układ ulic, które nie są do siebie ani równoległe, ani prostopadłe?

Film dostępny pod adresem /preview/resource/Rg6Frq85kL3bd
Animacja
Dwie półproste o wspólnym początku rozcinają płaszczyznę na dwie części. Każdą z tych części, wraz z tymi półprostymi nazywamy kątem.
Wierzchołkiem kąta nazywamy wspólny początek obu półprostych, a każdą z półprostych nazywamy ramieniem kąta.

Film dostępny pod adresem /preview/resource/R1ARgYOMMskFw
Animacja
Kąt prosty

Film dostępny pod adresem /preview/resource/R1MNhoTG37YHr
Animacja
Przygotuj kartkę papieru. Zegnij ją w dowolnym miejscu, a potem zegnij drugi raz, tak jak na rysunku. Mocno przyciśnij linie zgięć.

Rozegnij kartkę. Zobaczysz dwie linie prostopadłe. O dwóch prostych, które przecinają się w ten sposób będziemy mówili, że przecinają się pod kątem prostym.
Kąty ostre
Wskaż kąty, które nie są kątami prostymi.

Narysuj kąt prosty i kąt ostry.
Kąt półpełny, kąt rozwarty
Dwa kąty proste, mające wspólne ramię, położone tak, jak na rysunku, tworzą kąt półpełny.

Kąty, które są mniejsze od kąta półpełnego i większe od kąta prostego to kąty rozwarte.
Wskaż kąt rozwarty.
R1B7S1rv9T3Bf1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Narysuj trzy kąty rozwarte.
Kąt pełny, kąt wklęsły
Wskaż kąt wklęsły.

Narysuj trzy kąty wklęsłe.
Określ rodzaj kąta .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DHSNUAfKX
Kąt jest figurą geometryczną. Wyobraź sobie, że tniesz bardzo dużą płaską powierzchnię wzdłuż dwóch półprostych o wspólnym początku. W rezultacie otrzymasz dwa kąty. Jeżeli jeden będzie wklęsły, to drugi nie będzie wklęsły.
W kącie wyróżniamy: wierzchołek kąta, ramiona kąta oraz wnętrze kąta.
Ramiona kąta to dwie półproste o wspólnym początku.
Wierzchołek kąta to punkt.
Wskaż na rysunku wierzchołek kąta, ramiona kąta i wnętrze kąta ostrego.

Wskaż na rysunku wierzchołek kąta, ramiona kąta i wnętrze kąta wklęsłego.

Oto fragment planu Torunia.
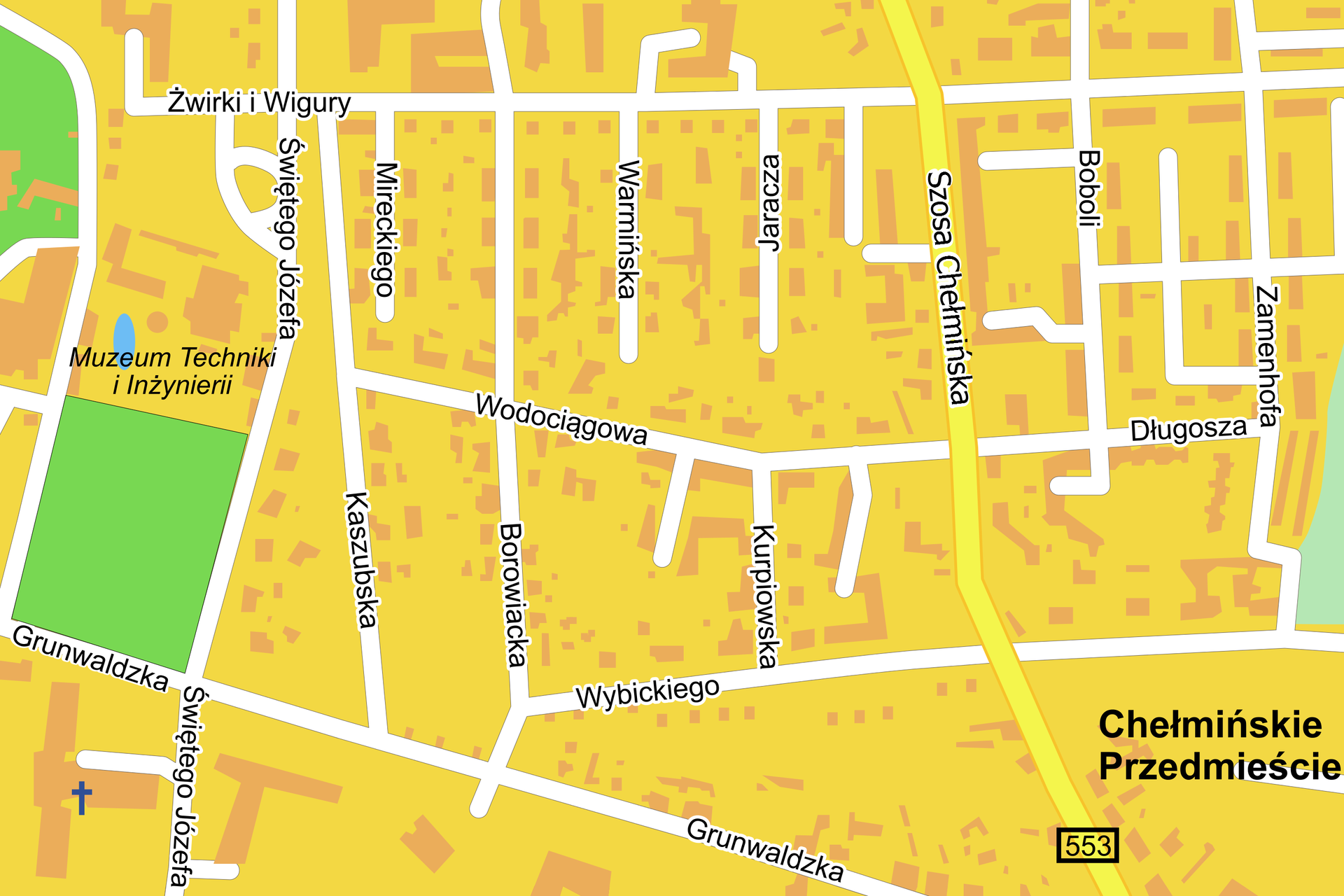
Czy to prawda, że
- ulice Borowiecka i Wybickiego przecinają się pod kątem ostrym?
- ulice Wodociągowa i Kaszubska przecinają się pod kątem rozwartym?
- ulice Wodociągowa i Kurpiowska przecinają się pod kątem rozwartym?
- ulice Zamenhofa i Długosza przecinają się pod kątem prostym?
Nazwij kąty, jakie tworzą wskazówki zegarów.
Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły czy pełny zakreśla wskazówka minutowa pomiędzy godzinami
ostry, prosty, prosty, rozwarty, półpełny, wklęsły, ostry, pełny, rozwarty, prosty, ostry, rozwarty, wklęsły, pełny, pełny, prosty, pełny, wklęsły, wklęsły, rozwarty, rozwarty, półpełny, półpełny, wklęsły, półpełny, prosty, ostry, pełny, ostry, ostry, pełny, rozwarty, półpełny, prosty, półpełny, wklęsły
a) 10:00, a 10:25? ......................
b) 16:15, a 16:46? ......................
c) 18:47, a 19:02? ......................
d) 22:45, a 23:31? ......................
e) 5:07, a 5:37? ......................
e)15:16, a 16:16? ......................
Jaki kąt: ostry, prosty, rozwarty, półpełny, wklęsły, czy pełny zakreśla wskazówka minutowa pomiędzy godzinami
wklęsły, ostry, półpełny, pełny, prosty, półpełny, ostry, prosty, wklęsły, rozwarty, rozwarty, półpełny, prosty, ostry, prosty, pełny, pełny, rozwarty, półpełny, rozwarty, pełny, wklęsły, prosty, wklęsły, półpełny, ostry, pełny, wklęsły, ostry, rozwarty
a) 7:28, a 8:28? ......................
b) 9:11, a 9:12? ......................
c) 12:35, a 13:24? ......................
d) 14:15, a 14:30? ......................
e) 17:48, a 18:18? ......................






