Symulacja interaktywna
Polecenie 1
Trójkąt, którego boki są liniami środkowymi, nazywamy trójkątem środkowym. Uruchom symulację i obserwuj zależność długości promienia okręgu opisanego na trójkącie środkowym od długości promienia okręgu opisanego na trójkącie .
Zapoznaj się z poniższym opisem apletu, w którym przedstawiono trójkąt, którego boki są liniami środkowymi. Jest to trójkąt środkowy D E F. Zwróć szczególną uwagę na zależność długości promienia okręgu opisanego na trójkącie środkowy D E F od długości promienia okręgu opisanego na trójkącie A B C.
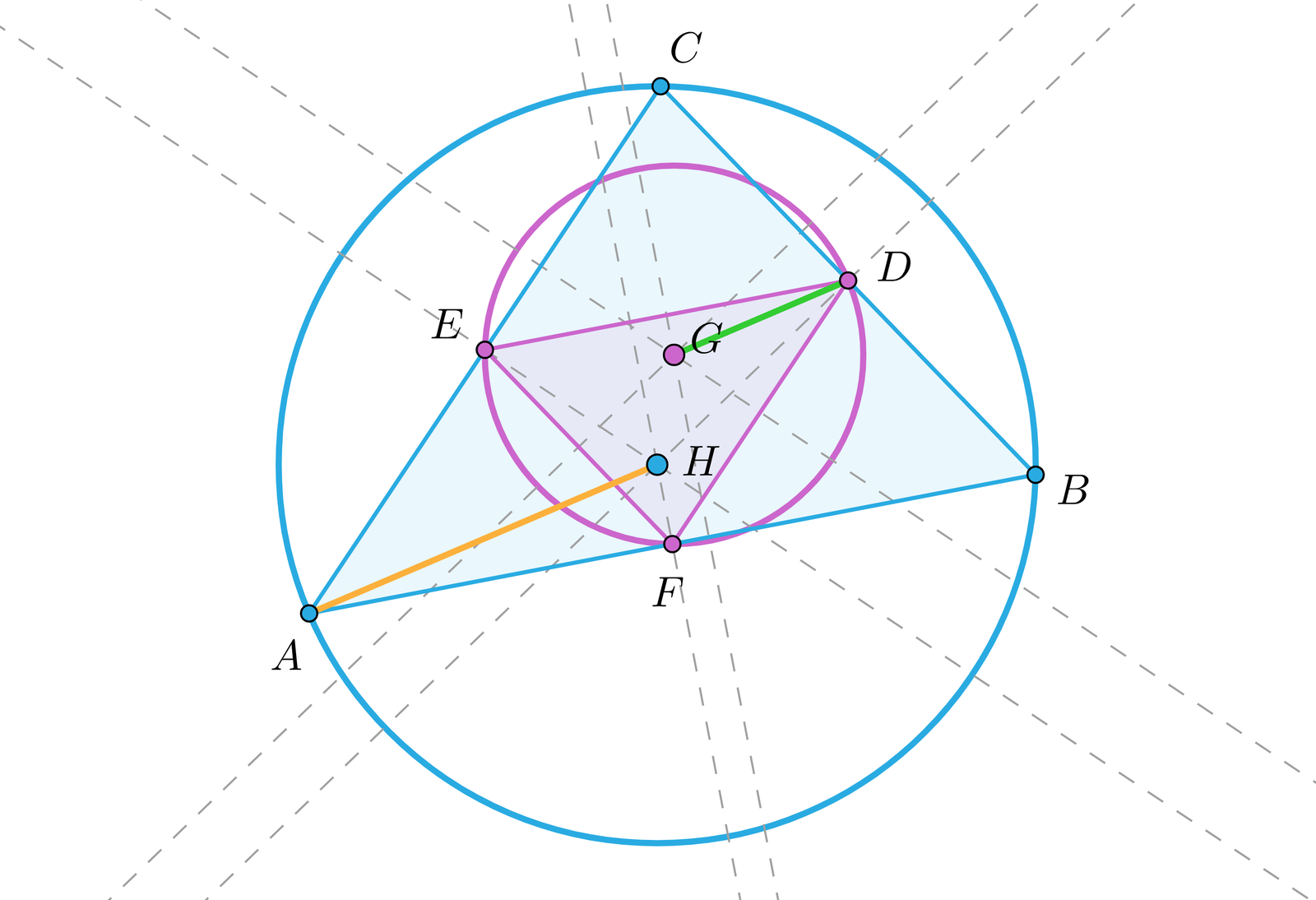
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DIXctkolM
Polecenie 2
Jaka jest zależność między długościami promieni okręgów opisanych na trójkącie i jego trójkącie środkowym? Odpowiedź uzasadnij.