Nierówności stopnia pierwszego

Nierówność otrzymamy, jeżeli między dwa wyrażenia algebraiczne wstawimy jeden ze znaków $<, >, \leq, \geq$ .
Nierównościami z jedną niewiadomą są, np.:

- 4 x + 6 \geq x - 4, 3 x^{2} + 5 > x - 1, a^{3} + 3 \leq a^{2} .

W tym dziale zajmować się będziemy rozwiązywaniem nierówności pierwszego stopnia (czyli liniowych) z jedną niewiadomą, np.:

x \leq 0, 2 x - 3 < 7, 1 - 3 x \geq 2 x + 2 .

Nierówność pierwszego stopnia (liniowa) z jedną niewiadomą

Definicja: Nierówność pierwszego stopnia (liniowa) z jedną niewiadomą

Nierównością pierwszego stopnia z jedną niewiadomą nazywamy nierówność, w której występuje dokładnie jedna niewiadoma w pierwszej potędze.
Na przykład

5 x + 3 \leq x - 1, - x + 3 > 9, 2 x + 4 \leq - x + 8, 7 y - 1 > 9,

2 (z - 3) \leq 7, (- 6 t - 6) : (- 2) \geq 2 t

Liczba spełniająca nierówność (rozwiązanie nierówności)

Definicja: Liczba spełniająca nierówność (rozwiązanie nierówności)

Mówimy, że liczba spełnia daną nierówność, jeżeli po wstawieniu jej w miejsce niewiadomej i wykonaniu wskazanych działań otrzymamy nierówność liczbową prawdziwą.
Na przykład:
Sprawdzimy, czy liczba $- 10$ spełnia nierówność $5 x + 3 < x - 1 .$
Podstawmy $- 10$ w miejsce $x .$

5 (- 10) + 3 < - 10 - 1

- 47 < - 11

Nierówność jest prawdziwa.
Liczba $- 10$ spełnia daną nierówność. Liczba $- 10$ jest jednym z rozwiązań nierówności.

Zbiór rozwiązań nierówności

Definicja: Zbiór rozwiązań nierówności

Zbiór rozwiązań nierówności jest to zbiór wszystkich liczb, które spełniają daną nierówność.

Przykład 1

R1EDrLhYanDz41

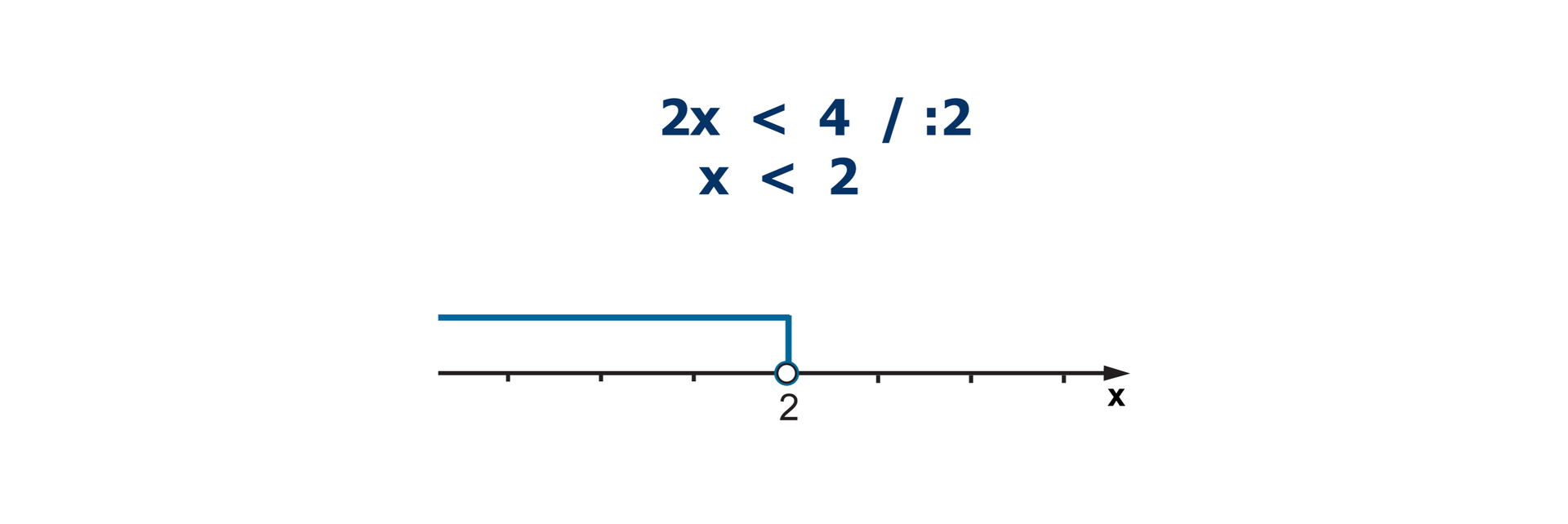
Nierówność: 2x < 4. Nierówność podzielona obustronnie przez 2. x < 2. Na osi liczbowej niezamalowane kółko w punkcie o współrzędnych 2. Zaznaczone wszystkie liczby mniejsze od 2. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Nierówności równoważne

Definicja: Nierówności równoważne

Nierówności nazywamy równoważnymi, jeżeli posiadają ten sam zbiór rozwiązań.

Przykład 2

Nierówności równoważne.

RYPDS7vCdvUYX1

Nierówność pierwsza: 2x < 4. Nierówność podzielona obustronnie przez 2. x < 2. Nierówność druga: 4x +3 < 3x +5. 4x -3x < 5 -3. x < 2. Dwie osie liczbowe z niezamalowanym kółkiem w punkcie o współrzędnych 2. Na obu osiach zaznaczone wszystkie liczby mniejsze od 2. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RhwPRDLvtFJ1h1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podczas rozwiązywania nierówności postępujemy podobnie jak przy rozwiązywaniu równań. Należy jednak zwrócić uwagę na mnożenie i dzielenie obydwu stron nierówności przez liczbę ujemną.

Zapamiętaj!

Rozwiązać nierówność to znaczy znaleźć wszystkie liczby, które spełniają tę nierówność lub wykazać, że nierówność nie ma rozwiązań. W tym celu możemy przekształcać nierówności równoważnie, pamiętając o tym, że

do obu stron nierówności możemy dodać lub od obu stron nierówności możemy odjąć tę samą liczbę lub wyrażenie,
obie strony nierówności możemy pomnożyć lub podzielić przez tę samą liczbę dodatnią,
obie strony nierówności możemy pomnożyć lub podzielić przez tę samą liczbę ujemną, pamiętając o zmianie znaku nierówności na przeciwny.

iBhY8cisei_d5e381

Ćwiczenie 1

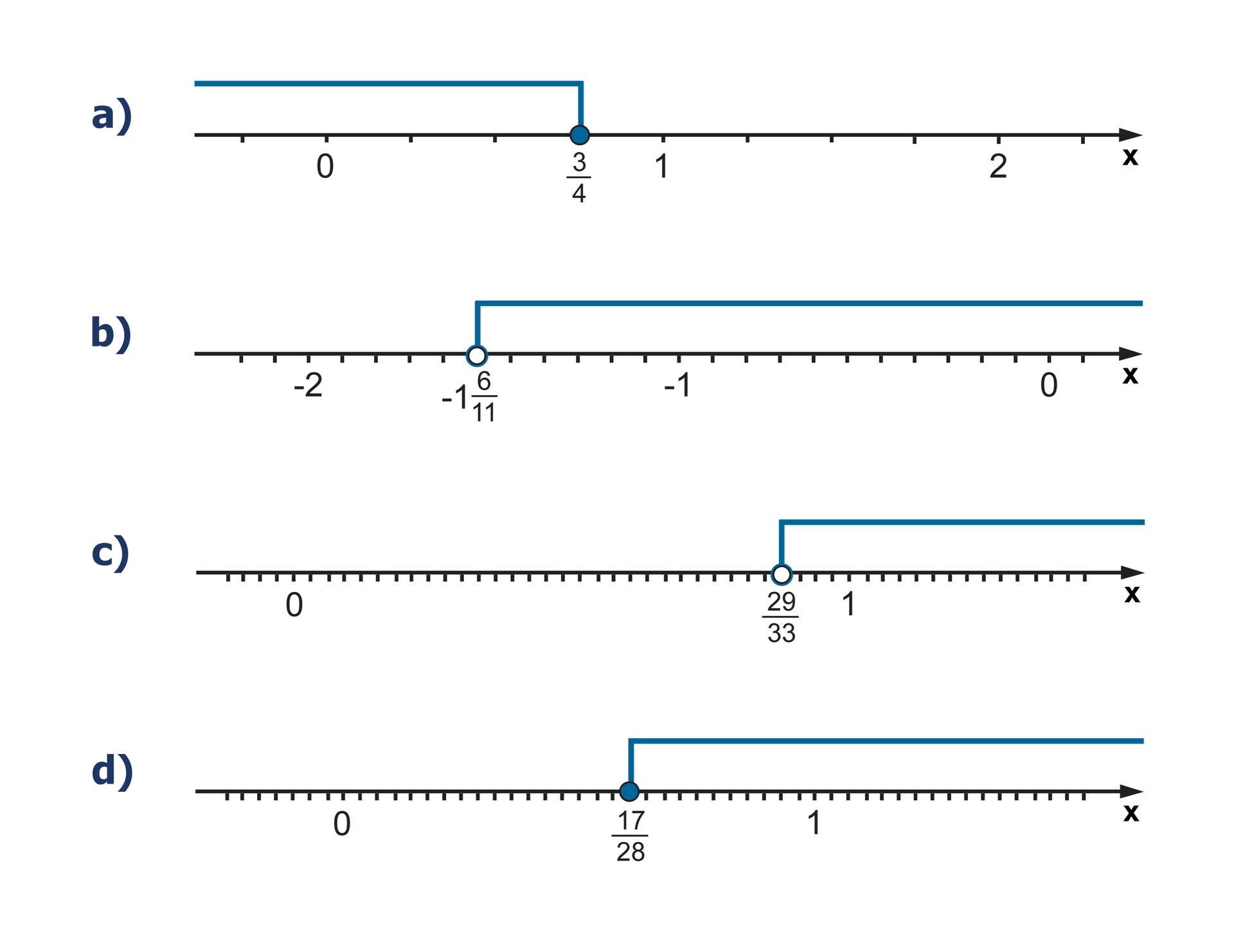
Zaznacz na osi liczbowej zbiór liczb spełniających daną nierówność.

$x \geq 4$
$x < 5$
$2 \leq x < 5$
$- 2 < x \leq 3$

Ćwiczenie 2

Zapisz nierówność, której zbiór rozwiązań zaznaczony jest na osi liczbowej.

RkZ8Q6UrNh0r01

Rysunki osi liczbowych. Na pierwszej osi zamalowane kółko w punkcie o współrzędnych 2. Zaznaczone wszystkie liczby w prawo od 2. Na drugiej osi niezamalowane kółko w punkcie o współrzędnych 4. Zaznaczone wszystkie liczby w lewo od 4. Na trzeciej osi zamalowane kółko punkcie o współrzędnych 0 i niezamalowane w punkcie 4. Zaznaczone wszystkie liczby między punktami 0 i 4. Na czwartej osi niezamalowane kółko w punkcie o współrzędnych -1 i zamalowane w punkcie 5. Zaznaczone wszystkie liczby między punktami -1 i 5. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

$x \geq 2$
$x < 4$
$0 \leq x < 4$
$- 1 < x \leq 5$

Ćwiczenie 3

RhnunzZ8U8uGa1

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Przeciągnij liczby spełniające daną nierówność z dolnej sekcji do górnej.

x \geq 6, 5

x < - 5

- 3 < x \leq 4, 5

5 \leq x \leq 6

- 5 \frac{1}{5}

5

- 5,001

- 2 \frac{2}{3}

- 8

6

8,3

4

4,25

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 4

R1B4rUu7j0lV11

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Przeciągnij liczby spełniające daną nierówność z dolnej sekcji do górnej.

x \leq - 1

x \geq 8

- 1 < x \leq 0

1 \leq x < 8

8

7 \frac{1}{4}

0

- 1 \frac{1}{3}

7

- 2

5

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 5

R14YPG1TX4d1D1

Trwa wczytywanie danych...

Rozwiąż i połącz nierówność z rozwiązaniem.

$2 x + 1 < 5$
$2 - 3 x \geq 1$
$3 (2 x - 4) > - 2 + x$
$2 x - 5 (x - 2) \leq 3$
$1 - 3 (2 x + 1) < 2 x + 3$
$5 x + 2 (x - 4) > x - 2$

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 6

R2uYJADbMeYLa1

Trwa wczytywanie danych...

Połącz w pary nierówności równoważne.

1−3x>2(x+2), 2x−3<4x+1, 2(1−x)>5, 2x+3(1−2x)>1−3x, 2+3(x+1)<2x, 1−2x<3−2(1−2x)

−2x
2x
−3x>2x+3
3x
1+2x>1−2x
x

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 7

R1bQ157gwsjyV1

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Przeciągnij i upuść tak, aby nierówności były równoważne.

2 x > 8

4 x >

x \leq 1

- 2 x

- 2

3 x - 1 < 5 x

2 x

- 1

1 - x \geq 2 - x

1 \geq

x + 2 < 2 x + 1

2 x + 4 <

2 - 3 x \leq 5

- 6 + 9 x \geq

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 8

R1PYZXg42hflb1

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Przeciągnij i upuść tak, aby nierówność była zawsze prawdziwa.

3 x + 2 > 3 x +

2 x - 3 \leq 2 x +

3 x + 2 > x +

x - 3 \leq 1 +

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 9

Rapu0K8CsWYzf1

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Przeciągnij i upuść tak, aby nierówność była sprzeczna.

3 x + 2 > 3 x +

2 x - 3 \leq 2 x +

3 x + 2 > x +

x - 3 \leq 1 +

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

iBhY8cisei_d5e683

classicmobile

Ćwiczenie 10

Nierówność, którą spełniają liczby $1, 2, 3$ , a nie spełniają $4, 5, 6$ to

R17TSB67nPItF

Trwa wczytywanie danych...

$2 (x + 2) > 10$
$2 (x + 2) < 10$
$2 (x + 2) \leq 10$
$2 (x + 2) \geq 10$

static

Ćwiczenie 10

Nierówność, którą spełniają liczby $1, 2, 3$ , a nie spełniają $4, 5, 6$ to

RpMq5S7kvBi3f

Trwa wczytywanie danych...

$2 (x + 2) > 10$
$2 (x + 2) < 10$
$2 (x + 2) \leq 10$
$2 (x + 2) \geq 10$

classicmobile

Ćwiczenie 11

Najmniejsza liczba całkowita spełniająca jednocześnie nierówność $\frac{x}{2} + 3 (x + 1) \geq 3$ i nierówność $3 - 8 (2 - x) < 2 x$ to

REVMn7gFRN7tK

Trwa wczytywanie danych...

$1$
$2$
$0$
$- 3$

static

Ćwiczenie 11

Najmniejsza liczba całkowita spełniająca jednocześnie nierówność $\frac{x}{2} + 3 (x + 1) \geq 3$ i nierówność $3 - 8 (2 - x) < 2 x$ to

R1PTiQffWnDuU

Trwa wczytywanie danych...

$1$
$2$
$0$
$- 3$

classicmobile

Ćwiczenie 12

Wybierz nierówność opisującą następującą sytuację:
Tabliczka kosztowała $x zł .$ Po podwyżce o $3 zł$ za $5$ tabliczek trzeba zapłacić więcej, niż za $6$ tabliczek przed podwyżką.

R1FZnqXVdiusG

Trwa wczytywanie danych...

$6 x < 5 (x + 3)$
$6 (x + 3) < 5 x$
$6 x > 5 (x + 3)$
$6 (x + 3) > 5 x$

static

Ćwiczenie 12

Wybierz nierówność opisującą następującą sytuację:
Tabliczka kosztowała $x zł .$ Po podwyżce o $3 zł$ za $5$ tabliczek trzeba zapłacić więcej, niż za $6$ tabliczek przed podwyżką.

RJWrqqTZny3RF

Trwa wczytywanie danych...

$6 x < 5 (x + 3)$
$6 (x + 3) < 5 x$
$6 x > 5 (x + 3)$
$6 (x + 3) > 5 x$

Ćwiczenie 13

Rozwiąż nierówność i zbiór rozwiązań przedstaw na osi liczbowej.

$2 + 3 (x - 2) \geq 1$
$3 (x + 3) - 2 (x - 2) < 5 x$
$2 x - 3 (1 - 3 x) + 2 \geq - 2 (x + 2)$
$3 - (2 - 3 x) - 4 (x - 2) > 5 (1 - x) + 2 x$

Ćwiczenie 14

Rozwiąż nierówność i zbiór rozwiązań przedstaw na osi liczbowej.

$\frac{x}{3} + \frac{2 x + 1}{2} \geq 2 x$
$\frac{x + 3}{2} + \frac{1 - x}{4} < 3 (x + 2)$
$2 x - \frac{x - 3}{5} > 3 + \frac{1 - 3 x}{2}$
$3 - \frac{2 - x}{3} - 2 x \leq \frac{x + 6}{5}$

Ćwiczenie 15

Rozwiąż nierówność $- 2 (x + 2) \geq 2 + 3 (x - 1)$ . Podaj największą liczbę całkowitą spełniającą tę nierówność.

$x \leq - \frac{3}{5}$ , największa liczba całkowita spełniająca nierówność to $- 1 .$

Ćwiczenie 16

Rozwiąż nierówność $2 x - 3 (x + 4) \leq - 3 x - 4$ . Podaj wszystkie liczby naturalne spełniające tę nierówność.

$x \leq 4$ , liczby naturalne to $0, 1, 2, 3, 4$ .

Ćwiczenie 17

Rozwiąż nierówność $\frac{x}{3} - \frac{x - 1}{2} \geq \frac{15 - 3 x}{3} - \frac{1}{2} (x + 4) .$
Podaj najmniejszą liczbę parzystą, która spełnia tę nierówność.

$x \geq 1 \frac{7}{8}$
najmniejsza liczba parzysta to $2$

Ćwiczenie 18

Lena kupiła opakowanie mazaków za $3,80 zł$ i pewną liczbę kolorowych piłek po $2,30 zł$ za sztukę. Ile maksymalnie kupiła piłek, jeżeli z $15 zł$ otrzymała niewielką resztę?

$x -$ liczba piłek
$3,80 + 2,30 ∙ x < 15 x < 4 \frac{20}{23}$ czyli $x = 4$

Ćwiczenie 19

Wypożyczalnia nart „Stok” oferuje wypożyczenie nart w cenie $15 zł$ za każdy dzień. Wypożyczalnia „Ski” oferuje za pierwszy dzień wypożyczenia nart cenę $35 zł$ , a za każdy kolejny dzień stałą cenę $8 zł$ . Na ile co najwyżej dni trzeba wypożyczyć narty, aby bardziej opłacało się skorzystać z oferty wypożyczalni „Stok”?

$15 x < 35 + (x - 1) 8$
$x < 3 \frac{6}{7}$
$3$ dni

Ćwiczenie 20

Suma cyfr liczby dwucyfrowej wynosi $8$ . Jeżeli przestawimy cyfry w tej liczbie, to otrzymana liczba jest nie większa od początkowej liczby. Jaka to liczba? Ile jest takich liczb?

$x -$ cyfra dziesiątek początkowej liczby, $10 x + (8 - x) \geq (8 - x) 10 + x$ , $x \geq 4$
$44, 53, 62, 71$

Ćwiczenie 21

R1EwahtG5d3lz1

OBIEKT MULTIMEDIALNY KLIKNIJ, ABY OTWORZYĆ NA PEŁNYM EKRANIE

Kliknij, aby rozpocząć

Wystąpił błąd

Spróbuj ponownie później

Uporządkuj etapy rozwiązywania nierówności.

Start:
Przekształcenie 1:
Przekształcenie 2:
Przekształcenie 3:
Przekształcenie 4:
Przekształcenie 5:
Przekształcenie 6:
Przekształcenie 7:
Koniec:

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wykorzystanie równań do rozwiązywania zadań tekstowych

Rozwiązywanie zadań tekstowych z wykorzystaniem równań i procentów