Graniastosłupy proste
Własności graniastosłupów prostych
Film dostępny na portalu epodreczniki.pl
Animacja pokazuje przykłady trzech figur przestrzennych, które są graniastosłupem o podstawie kwadratu, graniastosłupem o podstawie sześciokąta i graniastosłupem o podstawie trójkąta.
O graniastosłupie prostym mówiliśmy już w klasie piątej. Przypomnijmy jego definicję i własności.
Graniastosłup prosty to taka figura przestrzenna, która ma
dwie podstawy będące przystającymi (jednakowymi) wielokątami,
ściany boczne będące prostokątami.
Nazwa graniastosłupa zależy od rodzaju wielokąta w podstawie.
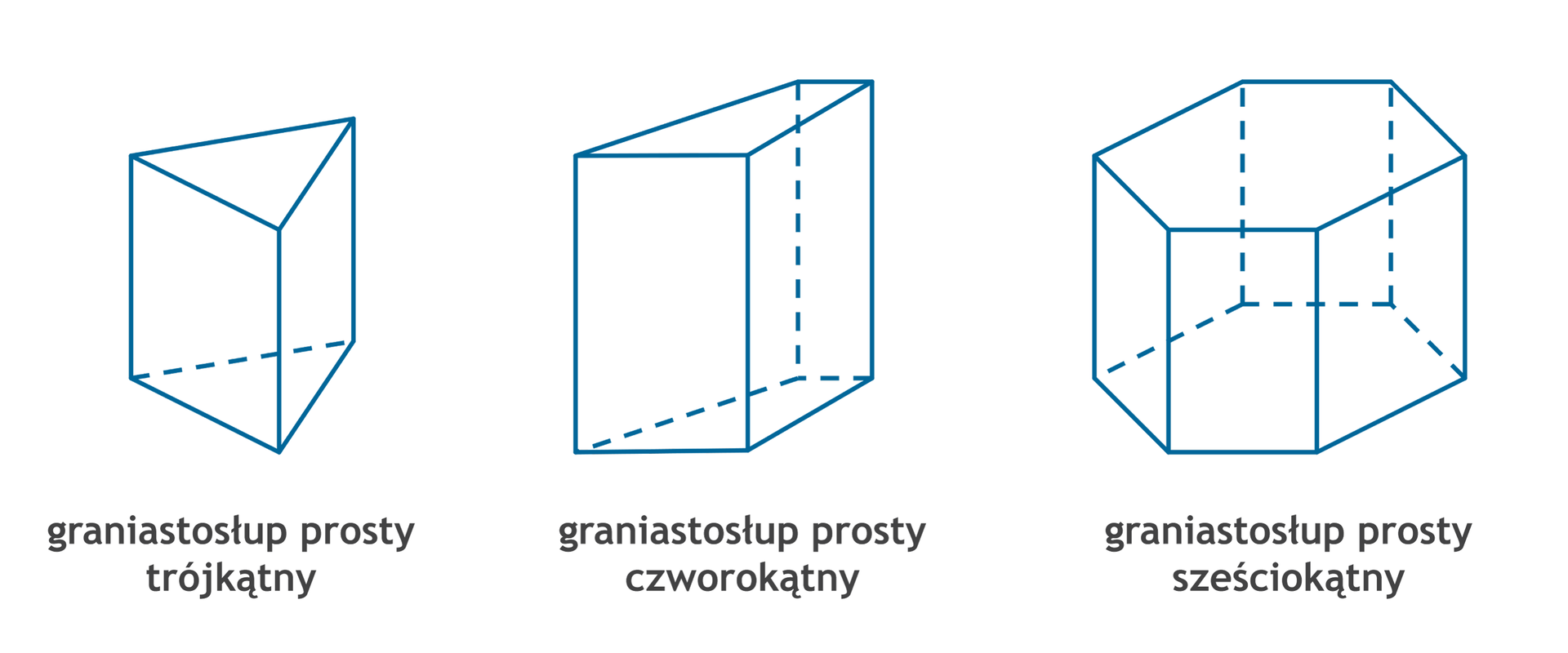
Obejrzyj dokładnie model graniastosłupa.

Rysujemy graniastosłupy i ich siatki
Siatka sześcianu
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje leżące na stole kostki do gry. Kreślone są krawędzie jednej kostki – powstaje sześcian. Dwa jednakowe sześciany rozkładają się na dwie różne siatki sześcianu.
Siatka sześcianu
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje dwie różne siatki sześcianu, które składają się w jednakowe sześciany. Sześcian zamienia się w kostkę do gry, która leży z innymi kostkami na stole.
Siatka prostopadłościanu
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje kolumny. Kreślone są krawędzie jednej kolumny – powstaje prostopadłościan. Dwa jednakowe prostopadłościany rozkładają się na dwie różne siatki prostopadłościanu.
Siatka prostopadłościanu
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje dwie różne siatki prostopadłościanu, które składają się w jednakowe prostopadłościany. Prostopadłościan zmienia się w kolumnę, która stoi obok innych kolumn.
Siatka graniastosłupa
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje nakrętki na śruby. Kreślone są krawędzie jednej nakrętki – powstaje graniastosłup o podstawie sześciokąta foremnego. Dwa jednakowe graniastosłupy rozkładają się na dwie różne siatki graniastosłupa.
Siatka graniastosłupa
Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje dwie różne siatki graniastosłupa, które składają się w jednakowe graniastosłupy. Graniastosłup zamienia się w nakrętkę leżącą między nakrętkami.
Narysuj w zeszycie siatkę graniastosłupa prostego, którego wysokość wynosi , a podstawą jest
trójkąt prostokątny o przyprostokątnych długości i
trójkąt równoramienny o ramionach długości i podstawie długości
romb o przekątnych długości i
trapez równoramienny o ramionach długości 4 cm i podstawach długości i
dowolny pięciokąt
Narysuj na kolorowej, grubszej kartce siatkę graniastosłupa prostego o podstawie rombu.
Przekątne rombu mają długości i , a długość krawędzi bocznej graniastosłupa wynosi .
Dorysuj skrzydełka, wytnij siatkę ze skrzydełkami i sklej model.
Możesz wykonać z kolegami i koleżankami następujące zadanie:
Wykorzystajcie kilka sklejonych modeli i zbudujcie z nich inne graniastosłupy. Podajcie nazwy otrzymanych graniastosłupów.
Jaką figurą może być podstawa otrzymanego graniastosłupa, jeżeli połączymy ścianami:
jednakowe modele
jednakowe modele graniastosłupów
Zadania
Krawędzie podstawy graniastosłupa prostego czworokątnego mają długości i , a krawędź boczna (wysokość graniastosłupa) ma długość . Ile wynosi suma długości wszystkich krawędzi tego graniastosłupa?
Suma długości wszystkich krawędzi graniastosłupa wynosi . Jaką długość ma wysokość tego graniastosłupa, jeżeli jego podstawą jest:
trójkąt o bokach długości i
romb o boku długości
Wybierz z listy poprawne odpowiedzi oraz ich uzasadnienia.
liczba wierzchołków graniastosłupa może być dowolną liczbą naturalną większą od 3., Tak, Nie, liczba wierzchołków graniastołupa jest zawsze parzysta., kwadrat jest prostokątem., Nie, Tak, Nie, kwadrat nie jest prostokątem, podstawy mogą być dowolnymi wielokątami., Nie, krawędzi jest 1,5 raza wicej niż wierzchołków., Tak, wszystkie ściany graniastosłupa są prostokątami., wierzchołków jest tyle samo co krawędzi., graniastosłup osiemnastokątny ma 54 krawędzie., graniastosłup dwudziestokątny ma 60 krawędzi.
a) W graniastosłupie prostym podstawy zawsze są prostokątami.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
b) W graniastosłupie prostym wierzchołków jest więcej niż krawędzi.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
c) W graniastosłupie prostym podstawy mogą być kwadratami.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
d) Istnieje graniastosłup prosty, który ma wierzchołków.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................
e) Istnieje graniastosłup prosty, który ma krawędzie oraz ścian.
........................................................................................................................................................................................ ponieważ ........................................................................................................................................................................................