Prezentacja multimedialna

Polecenie 1

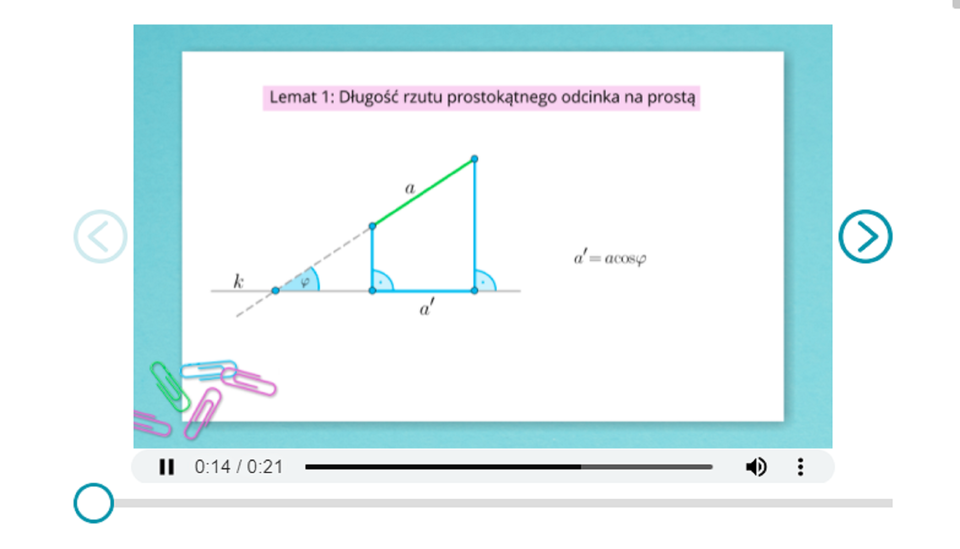
Odtwórz pierwszy fragment prezentacji i zapoznaj się z treścią lematu 1. dotyczącego długości rzutu prostokątnego odcinka na prostą. Po zapoznaniu się z tym lematem spróbuj przeprowadzić samodzielnie jego dowód. Po tym porównaj swój dowód z przedstawionym w kolejnym fragmencie prezentacji.

RNgV2ULK1Acdl
Lemat 1. Długość rzutu prostokątnego odcinka na prostą. Rysunek przedstawia trapez prostokątny o ramionach o długości a i a'. Trapez leży na ramieniu a'. Przez ramię a' przeprowadzono prostą k. Po przedłużeniu ramienia a powstał trójkąt. Kąt w punkcie przecięcia prostych ma miarę φ. Na prawo od rysunku zapisano równanie. a'=acosφ Napis. Dowód lematu jeden. Podpisano wierzchołki trapezu. Ramię o długości a oznaczono jako odcinek AB, ramię o długości a' oznaczono jako odcinek A'B'. Równolegle do prostej k poprowadzono prostą l przechodzącą przez wierzchołek A. Utworzono punkt C na podstawie trapezu. Kąt przy wierzchołku A wynosi φ. Lektor czyta równania zapisane na slajdzie.
AB=A'B'=a'
Miara kąta CAB wynosi φ.
Mamy
cosφ=ACAB=a'a a'=a·cosφ.
Dla φ=0 mamy
a'=a·1= a·cos0°=a·cosφ
Dla φ=90° mamy
a'=0=a·0= a·cos90°=a·cosφ Lemat 2. Napis. Długość boku trójkąta. Ilustracja przedstawia trójkąt ABC. Długość odcinka AB wynosi c, długość odcinka BC wynosi a, natomiast długość odcinka AC wynosi b. Kąt przy wierzchołku B ma miarę β, a kąt przy wierzchołku C ma miarę γ. Obok zapisano równanie czytane przez lektora. a=b·cosγ+c·cosβ
Kąt przy wierzchołku A ma miarę α. Z wierzchołka A poprowadzono odcinek AA'. Tworzy on z ramieniem BC kąt o mierze 90°. Odcinek podzielił trójkąt na dwa mniejsze. Nowopowstały trójkąt ABA' posiada podstawę o boku c.
Pojawiają się równania.
A'C=b·cosγ,
A'B=c·cosβ,
a=BC=A'C+A'B=b·cosγ+c·cosβ
Z punktu A poprowadzono odcinek do ramienia BA'. W miejscu przecięcia powstał punkt C. Długość odcinka BC wynosi a. Długość odcinka AC wynosi b. Przy wierzchołku C powstały dwa kąty przyległe, jeden ma miarę γ, drugi 180°-γ. Zatem mamy:
A'C=b·cos180°-γ=-b·cosγ
oraz
A'B=c·cosβ,
stąd
a=BC=A'B-A'C=c·cosβ--b·cosγ=c·cosβ+b·cosγ
Napis. Twierdzenie cosinusów. Ilustracja przedstawia trójkąt ABC o kątach wewnętrznych α,β,γ. Długość odcinka AB wynosi c, długość odcinka BC wynosi a, natomiast długość odcinka AC wynosi b. Pojawiają się równania.
a2=b2+c2-2bccosα.
Pojawia się układ równań.
a=b·cosγ+c·cosβb=a·cosγ+c·cosαc=a·cosβ +b·cosα
Pierwsze równanie mnożymy przez a, drugie przez b, trzecie przez c. Otrzymujemy
-a2=-ab·cosγ-ac·cosβb2=ab·cosγ+bc·cosαc2=ac·cosβ +bc·cosα
Sumujemy i redukujemy równania.
-a2+b2+c2=bc·cosα+bc·cosα,
co daje nam -a2+b2+c2=2bc·cosα,
a więc
a2=b2+c2-2bc·cosα

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DSPDUdkXc

Polecenie 2

Po zapoznaniu się z lematem 1. i jego dowodem, odtwórz kolejny fragment prezentacji i  przeanalizuj lemat 2.,  w którym podana jest zależność między długością boku trójkąta, długościami dwóch pozostałych boków i cosinusami kątów przy tym boku i, podobnie jak poprzednio, spróbuj samodzielnie przeprowadzić jego dowód. Zwróć uwagę, że spodek wysokości trójkąta może leżeć na boku trójkąta, ale może też leżeć na prostej zawierającej ten bok i nie leżeć na tym boku. Porównaj swój dowód z dowodem przedstawionym w następnych dwóch slajdach prezentacji.

Polecenie 3

Po zapoznaniu się z lematem 2. i jego dowodem odtwórz kolejny fragment prezentacji, w którym sformułowane zostało twierdzenie cosinusów. Tu również, spróbuj przeprowadzić dowód tego twierdzenia, wykorzystując w nim lemat 1. Porównaj swój dowód z dowodem przedstawionym w dalszej części filmu. Ta część została podzielona na fragmenty, w których pokazane są kolejne kroki dowodu. Gdyby nawet nie udało Ci się samodzielnie przeprowadzić dowodu, to odtwórz najpierw pierwszy fragment dowodu, spróbuj poprowadzić dowód dalej samodzielnie, jeśli to też Ci się nie uda, to postępuj tak z kolejnymi fragmentami prezentacji.

Przeczytaj
Sprawdź się