R12ScWMqniNOC

5. Podzielność w zbiorze liczb naturalnych - podsumowanie wiadomości

W jednej z egipskich piramid znaleziono kamienną płytę z wyrytą w postaci hieroglifu liczbą $2520$ .

Otóż $2520$ dzieli się przez wszystkie liczby naturalne od $1$ do $10$ . Nie istnieje mniejsza od $2520$ liczba naturalna różna od zera o tej własności. Liczba $2520$ jest więc najmniejszą wspólną wielokrotnością liczb $1$ , $2$ , $3$ , $4$ , $\dots$ , $9$ , $10$ .

W tym materiale będziemy poszukiwać najmniejszych wspólnych wielokrotności również innych liczb. Ale nie tylko – będziemy też rozpoznawać liczby pierwszeliczby pierwszeliczby pierwsze i złożoneliczby złożonezłożone, będziemy wyznaczać największy wspólny dzielnik kilku liczb, korzystając z cech podzielności. Zajmiemy się więc zagadnieniami związanymi z podzielnością liczb naturalnych.

Określimy dzielniki danej liczby, korzystając z cech podzielności, podamy kilka wielokrotności danej liczby, rozłożymy liczby na czynniki pierwsze, znajdziemy największy wspólny dzielnik oraz najmniejszą wspólną wielokrotność liczb naturalnych.

Liczbę $63$ można zapisać w postaci $63 = 7 \cdot 9$ . Liczba $63$ jest podzielna przez $7$ i przez $9$ , liczby $7$ i $9$ to dzielniki liczby $63$ . Liczba ta ma więcej dzielników. Zapisujemy:

D_{63} = \{1, 3, 7, 9, 21, 63\}

Każda liczba naturalna ma co najmniej jeden dzielnik.
Liczba $1$ jest dzielnikiem każdej liczby naturalnej.
Liczba $0$ ma nieskończenie wiele dzielników.

Przykład 1

Julka ma $16$ jabłek, $24$ gruszki i $8$ pomarańczy. Chce owoce rozdzielić między cztery koleżanki tak, aby każda z dziewcząt dostała taką samą liczbę owoców. Obliczymy, po ile owoców dostanie każda z dziewcząt.

Julka może podzielić owoce dwoma sposobami.
Może wymieszać wszystkie owoce i podzielić je na cztery równe części.

16 + 24 + 8 = 48

48 : 4 = 12

W tym przypadku każda z dziewcząt dostanie po $12$ owoców.
Może też podzielić je tak, aby każda z dziewcząt dostała po tyle samo owoców każdego rodzaju.
Zauważmy, że każda z liczb $16$ , $24$ , $8$ dzieli się przez $4$ .

16 : 4 = 4

24 : 4 = 6

8 : 4 = 2

W tym przypadku każda z dziewcząt dostanie $4$ jabłka, $6$ gruszek i $2$ pomarańcze.

Korzystając z powyższego przykładu powiemy, że liczba $4$ jest wspólnym dzielnikiem liczb $16$ , $24$ , $8$ .
Liczby te mają jeszcze dwa inne wspólne dzielniki: $1$ i $8$ . Liczba $8$ jest największym wspólnym dzielnikiem tych liczb. Zapisujemy:

N W D (8, 16, 24) = 8

Jeżeli największy wspólny dzielnik dwóch liczb jest równy $1$ , to liczby te nazywamy względnie pierwszymi.

Przykład 2

Ustalimy, które z liczb: $10$ i $12$ , $12$ i $30$ , $14$ i $15$ tworzą parę liczb względnie pierwszych.
W tym celu wyznaczymy NWD każdej pary liczb.

N W D (10, 12) = 2

N W D (12, 30) = 6

N W D (14, 15) = 1

Tylko w przypadku liczb $14$ i $15$ największy wspólny dzielnik jest równy $1$ , zatem te liczby tworzą parę liczb względnie pierwszych.

Zauważmy, że liczba $10$ jest dzielnikiem każdej z liczb $70$ , $110$ , $200$ , $350$ . Możemy powiedzieć, że liczby $70$ , $110$ , $200$ , $350$ to wielokrotności liczby $10$ . Zapisujemy:

W_{10} = \{70, 110, 200, 350, \dots\}

Liczby, które są wielokrotnościami $2$ , nazywamy liczbami parzystymiliczby parzysteliczbami parzystymi.
Pozostałe liczby naturalne, to liczby nieparzyste.
Liczby parzyste to na przykład: $0$ , $8$ , $12$ , $150$ , $2024$ .
Liczby nieparzyste to na przykład: $1$ , $7$ , $9$ , $13$ , $127$ .
Każda liczba naturalna dodatnia ma nieskończenie wiele wielokrotności. Liczba zero jest wielokrotnością każdej liczby naturalnej.

Przykład 3

Wyznaczymy kilka początkowych wielokrotności liczb: $3$ , $5$ , $6$ , $11$ .

W_{3} = \{0, 3, 6, 9, 12, 15, 18, \dots\}

W_{5} = \{0, 5, 10, 15, 20, 25, 30, 35, \dots\}

W_{6} = \{0, 6, 12, 18, 24, 30, 36, 42, \dots\}

W_{11} = \{0, 11, 22, 33, 44, 55, 66, \dots\}

Liczba $6$ jest wielokrotnością każdej z liczb $2$ , $3$ , $6$ . Mówimy, że jest wspólną wielokrotnością tych liczb

Liczby $2$ , $3$ , $6$ mają też inne wspólne wielokrotności, np.: $24$ , $48$ , $60$ . Jednak liczba $6$ jest najmniejszą wspólną wielokrotnością, różną od zera, tych liczb.
Zapisujemy:

N W W (2, 3, 6) = 6

Przykład 4

Wyznaczymy najmniejszą wspólną wielokrotność liczb $42$ , $105$ , $126$ .
Wypisujemy kilka kolejnych wielokrotności każdej z podanych liczb.

W_{42} = \{0, 42, 84, \dots, 588, 630, 672, \dots\}

W_{105} = \{0, 105, 210, 315, 420, 525, 630, \dots\}

W_{126} = \{0, 126, 252, 378, 504, 630, 756, \dots\}

Najmniejszą liczbą, która jest wielokrotnością każdej z liczb $42$ , $105$ , $126$ jest $630$ .

N W W (42, 105, 126) = 630

Każda liczba różna od $1$ ma co najmniej dwa dzielniki.
Liczby, które mają tylko dwa dzielniki (liczbę $1$ i samą siebie) nazywamy liczbami pierwszymiliczby pierwszeliczbami pierwszymi.
Liczby większe od $1$ , które mają więcej niż dwa dzielniki nazywamy liczbami złożonymiliczby złożoneliczbami złożonymi.
Liczby $0$ i $1$ nie są ani liczbami pierwszymi, ani złożonymi.

Przykład 5

Liczby jednocyfrowe pierwsze to: $2$ , $3$ , $5$ , $7$ .
Liczby jednocyfrowe złożone to: $4$ , $6$ , $8$ , $9$ .
Niektóre liczby dwucyfrowe pierwsze to: $11$ , $13$ , $17$ , $19$ , $23$ .

Każdą liczbę złożoną można rozłożyć na czynniki pierwsze, czyli zapisać ją za pomocą iloczynu liczb pierwszychiloczyn liczb pierwszychiloczynu liczb pierwszych.

Przykład 6

Rozłożymy na czynniki pierwsze liczbę $882$ .
Dzielimy $882$ przez kolejne jej dzielniki, będące liczbami pierwszymiliczby pierwszeliczbami pierwszymi. Dzielniki zapisujemy po prawej stronie pionowej kreski, a otrzymane ilorazy po lewej stronie. Postępujemy tak długo, aż otrzymany iloraz będzie równy $1$ .

R10Gtm2iXUyHd

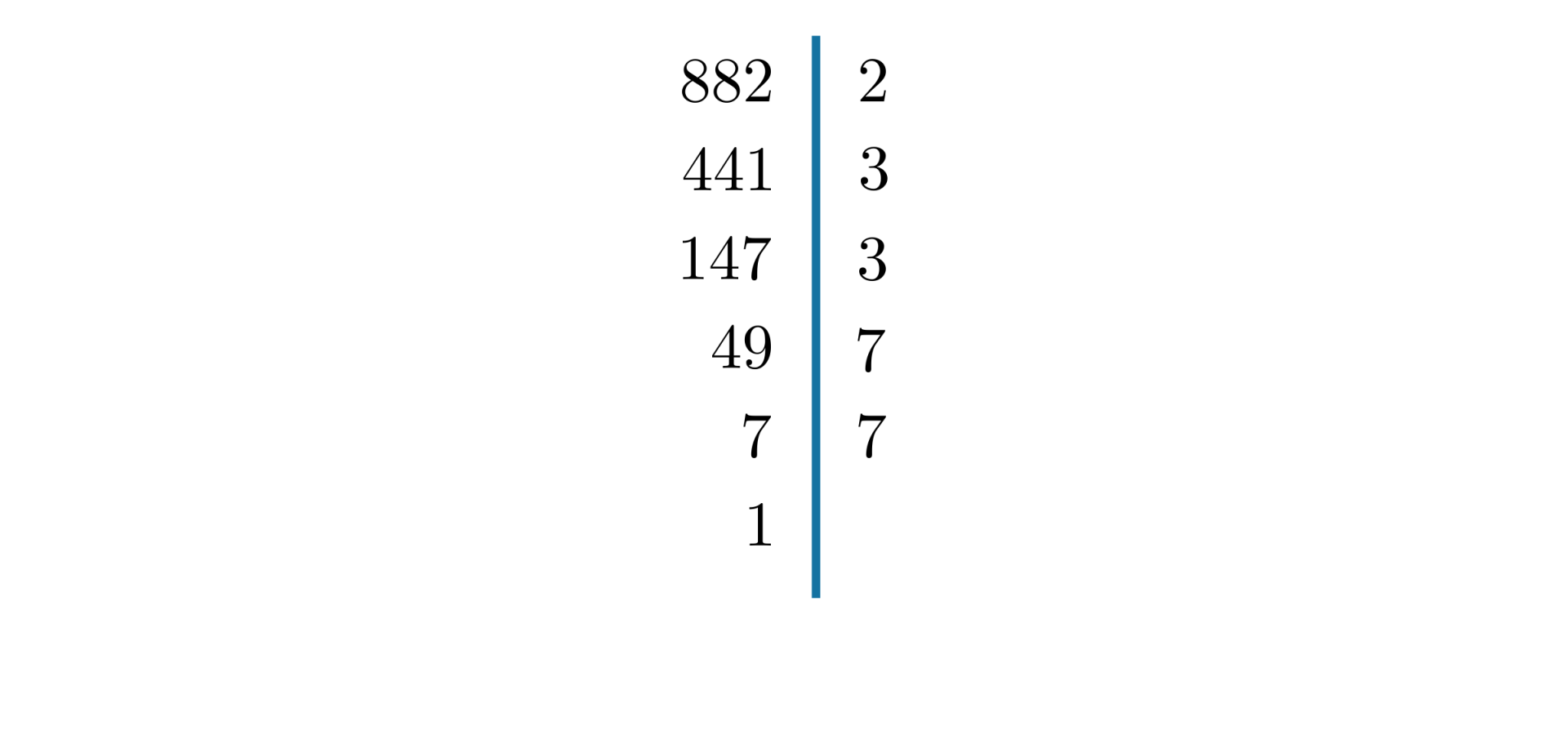
Rozkład liczby 882 na czynniki pierwsze. Dzielniki zapisujemy po prawej stronie pionowej kreski, a otrzymane ilorazy po lewej stronie. Po lewej stronie w formie kolumny zapisane są następujące liczby: 882, 441, 147, 49, 7, 1. Po prawej stronie w formie kolumny zapisane są następujące liczby: 2, 2, 3, 3, 7. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Zapisujemy: $882 = 2 \cdot 3 \cdot 3 \cdot 7 \cdot 7$

Rozkład liczby na czynniki pierwsze, możemy wykorzystać do znalezienia NWD i NWW danych liczb.

Przykład 7

Znajdziemy NWD i NWW liczb $210$ i $462$ .
Rozkładamy każdą z liczb $210$ i $462$ na czynniki pierwsze.

R1525rPiequkR

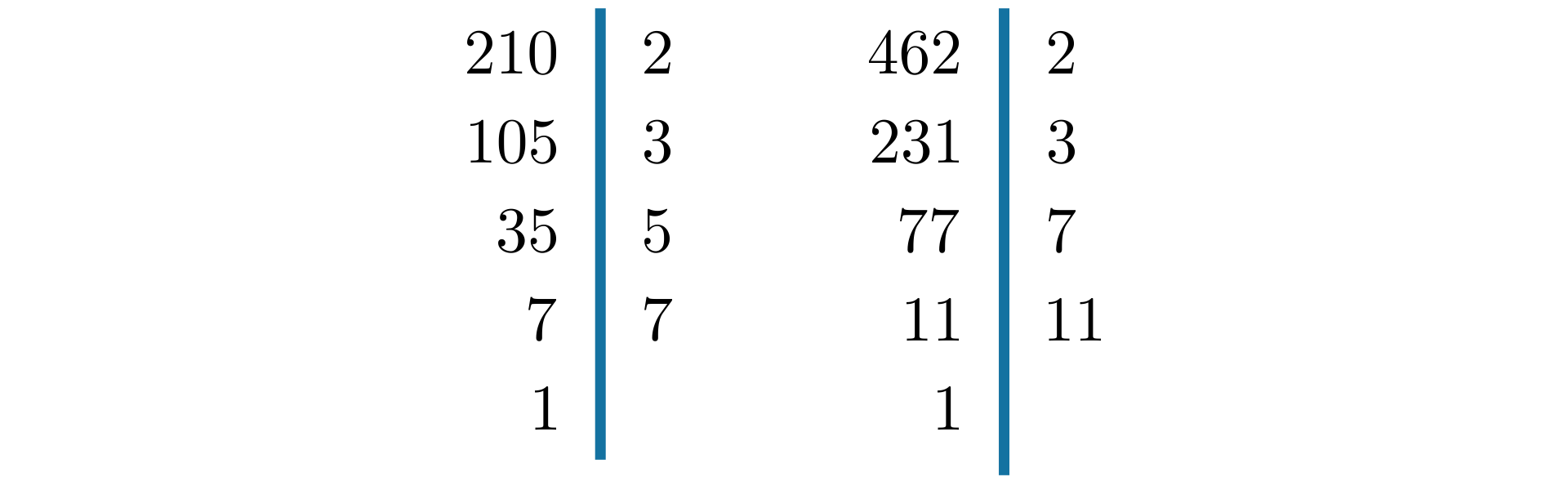
Po lewej stronie zrzutu ekranu ukazany jest rozkład liczby 210 na czynniki pierwsze. Dzielniki zapisujemy po prawej stronie pionowej kreski, a otrzymane ilorazy po lewej stronie. Po lewej stronie w formie kolumny zapisane są następujące liczby: 210, 105, 35, 7, 1. Po prawej stronie w formie kolumny zapisane są następujące liczby: 2, 3, 5, 7. Po prawej stronie zrzutu ekranu ukazany jest rozkład liczby 462 na czynniki pierwsze. Po lewej stronie w formie kolumny zapisane są następujące liczby: 462, 231, 77, 11, 1. Po prawej stronie w formie kolumny zapisane są następujące liczby: 2, 3, 7, 11. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wspólnymi czynnikami tych rozkładów są liczby: $2$ , $3$ , $7$ .

N W D (210, 462) = 2 \cdot 3 \cdot 7 = 42

Aby znaleźć najmniejszą wspólną wielokrotność liczb $210$ i $462$ wypisujemy wszystkie czynniki obu rozkładów. Wspólne czynniki wypisujemy tylko raz. Najmniejsza wspólna wielokrotność to iloczyn wypisanych liczb.

N W W (210, 462) = 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2310

Poszukując dzielników liczb naturalnych, warto skorzystać z reguł, zwanych cechami podzielności.
Liczba dzieli się przez	Cechy podzielności
$2$	jeśli cyfrą jedności tej liczby jest $0$ , $2$ , $4$ , $6$ lub $8$
$3$	jeśli suma cyfr tej liczby jest podzielna przez $3$
$4$	jeśli dwie ostatnie cyfry tej liczby tworzą liczbę podzielną przez $4$ lub obie są zerami
$5$	jeśli cyfrą jedności tej liczby jest $0$ lub $5$
$9$	jeśli suma cyfr tej liczby jest podzielna przez $9$
$10$	jeśli cyfrą jedności tej liczby jest $0$
$25$	jeśli dwie ostatnie cyfry tej liczby tworzą liczbę podzielną przez $25$ lub obie są zerami
$100$	jeśli cyfrą jedności i cyfrą dziesiątek tej liczby jest $0$

Przykład 8

Znajdziemy kilka dzielników liczby $1500$ .

Skorzystamy z cech podzielności.

Cyfrą jedności liczby $1500$ jest $0$ , więc liczba ta dzieli się przez $2$ , przez $5$ i przez $10$ .
Suma cyfr tej liczby to $1 + 5 + 0 + 0 = 6$ , więc liczba ta dzieli się przez $3$ .
Dwie ostatnie cyfry tej liczby to zera, zatem liczba dzieli się przez $4$ , $25$ i $100$ .
Każda z liczb naturalnych dzieli się też przez $1$ i samą siebie, zatem dwa następne dzielniki liczby $1500$ to $1$ i $1500$ .

D_{1500} = \{1, 2, 3, 4, 5, \dots, \dots 10, \dots, 25, \dots, \dots, 100, \dots, 1500\}

Polecenie 1

Zagraj w poniższą grę oraz wykonaj polecenia zapisane pod grą.

R17YeRHuEAKAA

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Podzielność w zbiorze liczb naturalnych3080Brawo! Test zaliczony. Znasz temat podzielności w zbiorze liczb naturalnych.Niestety, nie udało Ci się zaliczyć testu. Przeanalizuj przykłady zawarte w materiale ponownie i spróbuj rozwiązać test jeszcze raz.

Test

Podzielność w zbiorze liczb naturalnych

Liczba pytań:

Limit czasu:

30 min

Pozostało prób:

1/1

Twój ostatni wynik:

Podzielność w zbiorze liczb naturalnych

Pytanie 1/20

Twój ostatni wynik -

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Polecenie 2

Do największej liczby dwucyfrowej, która nie jest podzielna ani przez $2$ , ani przez $3$ , ani przez $4$ , ani przez $5$ , ani przez $6$ , ani przez $7$ dodano $8$ . Wykaż, że liczba ta jest podzielna przez $5$ .

Największa liczba dwucyfrowa, która nie jest podzielna ani przez $2$ , ani przez $3$ , ani przez $4$ , ani przez $5$ , ani przez $6$ , ani przez $7$ to największa liczba pierwsza dwucyfrowa.

Największa liczba dwucyfrowa, która nie jest podzielna ani przez $2$ , ani przez $3$ , ani przez $4$ , ani przez $5$ , ani przez $6$ , ani przez $7$ to największa liczba pierwsza dwucyfrowa, czyli $97$ . $97 + 8 = 105$ .

Cyfrą jedności liczy $105$ jest $5$ , więc jest to liczba podzielna przez $5$ , co należało wykazać.

Polecenie 3

Uzasadnij, że suma dwóch liczb pierwszych większych od $2$ jest liczbą parzystą.

Każda liczba naturalna pierwsza, większa od $2$ , jest liczbą nieparzystą.

Każda liczba naturalna pierwsza, większa od $2$ , jest liczbą nieparzystą. Suma dwóch liczb nieparzystych jest liczbą parzystą, co należało wykazać.

Polecenie 4

Uzasadnij, że liczba $17145$ jest podzielna przez $15$ .

Jeżeli liczba naturalna dodatnia jest podzielna przez $3$ i przez $5$ , to jest podzielna przez $15$ .

Liczba $17145$ jest podzielna przez $3$ , bo suma jej cyfr to $18$ : $1 + 7 + 1 + 4 + 5 = 18 = 3 \cdot 6$ .

Liczba $18$ jest podzielna przez $3$ .

Cyfra jedności liczby $17145$ to $5$ , zatem liczba ta jest podzielna przez $5$ .

Liczba $17145$ jest podzielna przez $3$ i przez $5$ , zatem jest podzielna przez $15$ .

R11ysNOA08bed

Ćwiczenie 1

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R8nG69z3uUmVa

Ćwiczenie 2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

R1Pn095O0CVEr

Ćwiczenie 3

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RH9lRTxk2Hkp5

Ćwiczenie 4

Połącz każdą z liczb z kilkoma jej wielokrotnościami.

3

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

10

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

13

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

7

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

8

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

11

Możliwe odpowiedzi: 1.

21

28

42

63

77

, 2.

0

8

24

56

80

, 3.

0

10

20

30

40

50

, 4.

33

121

143

165

, 5.

0

3

6

9

12

15

, 6.

0

13

26

39

169

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RIcgMWBuC8C8W

Ćwiczenie 5

Łączenie par. Zaznacz, które zdanie jest prawdziwe, a które fałszywe.. Najmniejszą liczbą nieparzystą jest liczba

3

.. Możliwe odpowiedzi: Prawda, Fałsz. Liczbą która nie jest ani liczbą pierwszą, ani złożoną jest liczba

0

.. Możliwe odpowiedzi: Prawda, Fałsz. Liczba, która jest dzielnikiem każdej liczby naturalnej to

1

.. Możliwe odpowiedzi: Prawda, Fałsz. Liczba

738

jest wielokrotnością liczby

6

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeżeli liczba jest podzielna przez

10

, to jest podzielna przez

3

.. Możliwe odpowiedzi: Prawda, Fałsz. Jeżeli liczba jest podzielna przez

5

i przez

2

to jest podzielna przez

10

.. Możliwe odpowiedzi: Prawda, Fałsz

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RVYwpde5B1Zs8

Ćwiczenie 6

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 7

W zamkowych komnatach stoją cztery zegary. Pierwszy zegar bije co dwie godziny, drugi co sześć godzin, trzeci co kwadrans, a czwarty co dwanaście godzin. Oblicz, co ile godzin te zegary biją równocześnie.

R473RLN2YUmFR

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Wyznacz najmniejszą wspólną wielokrotność liczb $2$ , $6$ i $12$ .

Wyznaczamy najmniejszą wspólną wielokrotność liczb $2$ , $6$ , $12$ .

N W W (2, 6, 12) = 12

Zegar, który bije co kwadrans, bije zawsze również o pełnych godzinach.

Odpowiedź:
Zamkowe zegary biją równocześnie co $12$ godzin.

Ćwiczenie 8

Znajdź największy wspólny dzielnik liczb $40$ , $135$ , $100$ .

RHnrT9AhCbIzv

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rozkładamy każdą z liczb $40$ , $135$ , $100$ na czynniki pierwsze.

40 = 2 \cdot 2 \cdot 2 \cdot 5

135 = 3 \cdot 3 \cdot 3 \cdot 5

100 = 2 \cdot 2 \cdot 5 \cdot 5

Jedyny wspólny dzielnik liczb $40$ , $135$ , $100$ to $5$ .

N W D (40, 135, 100) = 5

Słownik

liczby parzyste

Liczby, które są wielokrotnościami $2$ , nazywamy liczbami parzystymi.

liczby pierwsze

Liczby, które mają tylko dwa dzielniki (liczbę $1$ i samą siebie) nazywamy liczbami pierwszymi.

liczby złożone

Liczby, większe od $1$ , które mają więcej niż dwa dzielniki nazywamy liczbami złożonymi.

iloczyn liczb pierwszych

Rozłożyć liczby na czynniki pierwsze, to zapisać tę liczbę za pomocą iloczynu liczb pierwszych.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

4. Rozkład liczby na czynniki pierwsze

6. Liczby naturalne - pożegnanie

5. Podzielność w zbiorze liczb naturalnych - podsumowanie wiadomości

Podzielność w zbiorze liczb naturalnych

Słownik

Notatnik

4. Rozkład liczby na czynniki pierwsze

6. Liczby naturalne - pożegnanie

Własności liczb naturalnych

5. Podzielność w zbiorze liczb naturalnych - podsumowanie wiadomości

Podzielność w zbiorze liczb naturalnych

Słownik

Notatnik