Przeczytaj

Na początku przeanalizujemy własności okręgu opisanego na trójkącie.

R152iGZDSHcXS

Film dostępny pod adresem https://zpe.gov.pl/a/DeDBzXJiR

Film nawiązujący do treści materiału. Własności okręgu opisanego na trójkącie.

Przykład 1

Wykorzystując własności kątów wpisanych udowodnimy, że pole trójkąta o bokach długości $a$ , $b$ , $c$ wpisanego w okrąg o promieniu $R$ wyraża się wzorem:

P = \frac{a b c}{4 R}

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku:

R17uGZbRyJ3xw

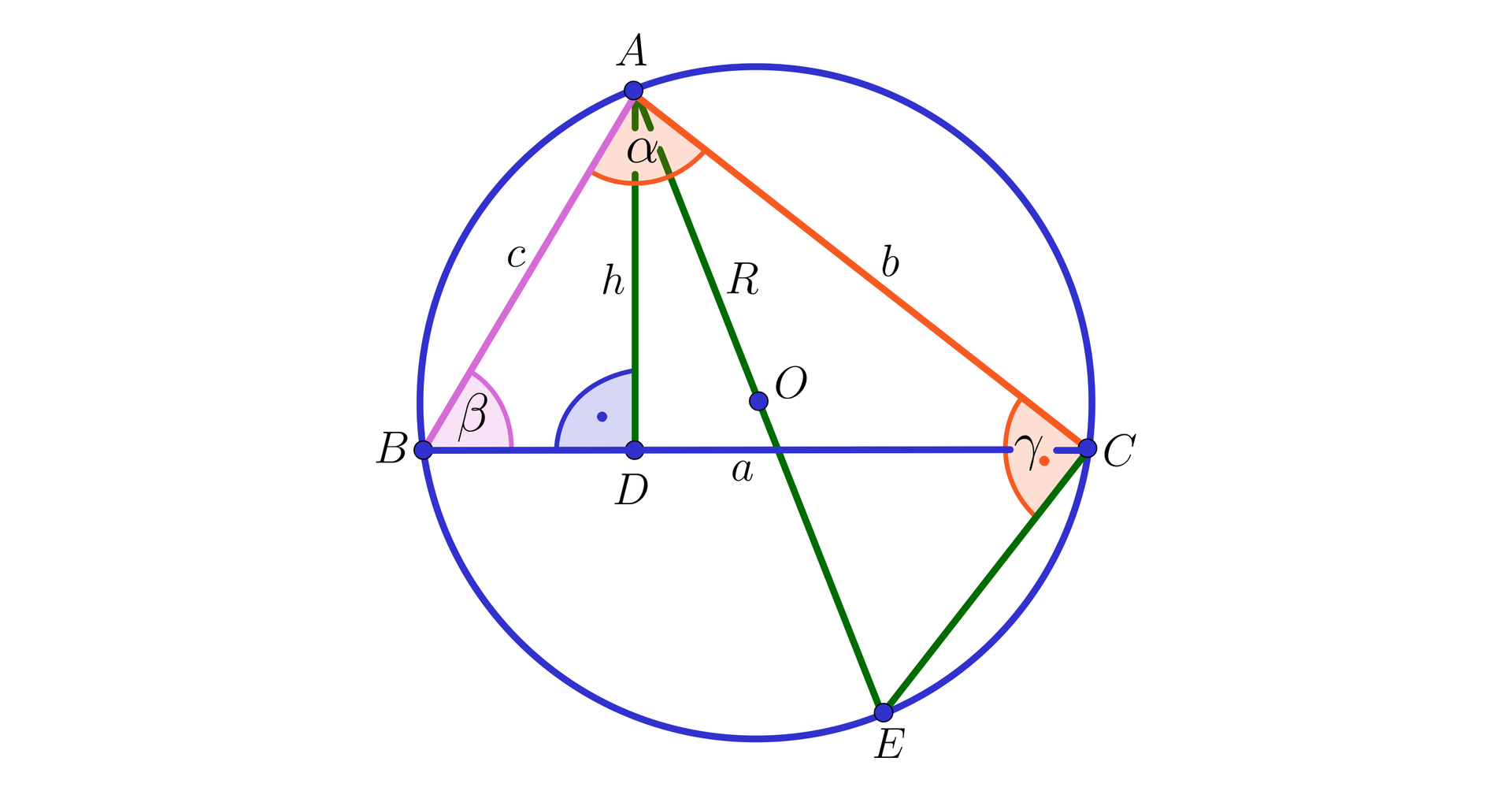
Ilustracja przedstawia trójkąt A B C, który został wpisany w okrąg o środku O. Z wierzchołka A przez punkt O poprowadzono odcinek, którego koniec leży na okręgu i jest podpisany literą E. Z wierzchołka A na bok BC opuszczono wysokość h, której spodek podpisano literą D. Odcinek AB podpisano literą c. Odcinek BC podpisano literą a. Odcinek AC podpisano literą b. Odcinek AO podpisano literą R. Kąt BAC podpisano literą alfa. Kąt CBA podpisano literą beta. Kąt EC podpisano literą gamma. Wierzchołki A C E tworzą trójkąt.

Trójkąt $A B C$ o bokach długości $a$ , $b$ , $c$ jest wpisany w okrąg o środku $O$ i promieniu $R$ . Odcinek $A D$ jest wysokością trójkąta, a odcinek $A E$ jest średnicą okręgu. Kąty $A B C$ oraz $A E C$ są kątami wpisanymi, opartymi na tym samym łuku, zatem mają takie same miary. Stąd trójkąty $A B D$ i $A E C$ są podobne, czyli: $\frac{h}{c} = \frac{b}{2 R}$ , zatem $h = \frac{b c}{2 R}$ .

P = \frac{1}{2} a h = \frac{1}{2} a \cdot \frac{b c}{2 R} = \frac{a b c}{4 R}

Warto przypomnieć wzór Herona, który pozwala obliczyć pole dowolnego trójkąta, gdy znamy długości wszystkich jego boków.

Jeżeli $0 < a \leq b \leq c$ są długościami boków trójkąta oraz $p = \frac{a + b + c}{2}$ , to pole trójkąta możemy obliczyć ze wzoru:

P_{△} = \sqrt{p (p - a) (p - b) (p - c)}

Przykład 2

Obliczymy pole trójkąta wpisanego w okrąg,trójkąt wpisany w okrągtrójkąta wpisanego w okrąg, którego boki są długości: $4 cm$ , $13 cm$ i $15 cm$ , wiedząc, że promień tego okręgu jest równy $8, 125 cm$ .

Rozwiązanie

$I$ sposób:

Korzystając ze wzoru $P = \frac{a b c}{4 R}$ , otrzymujemy:

$P = \frac{4 \cdot 13 \cdot 15}{4 \cdot 8, 125} = \frac{780}{32, 5} = 24 [{cm}^{2}]$

$II$ sposób:

R18FMZ5fFV2v5

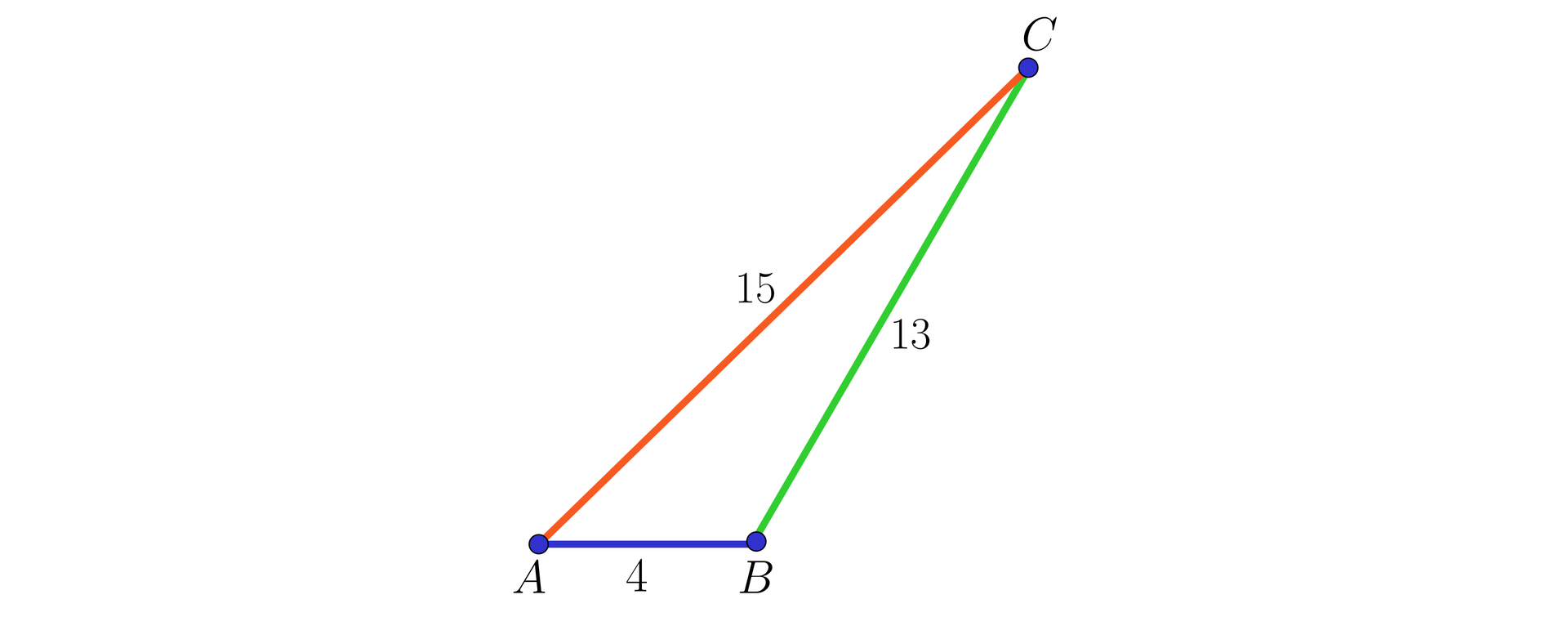
Ilustracja przedstawia trójkąt A B C. Bok AB ma długość 4, bok AC ma długość 15, a bok BC ma długość trzynaście.

Korzystając ze wzoru Herona najpierw obliczymy $p = \frac{4 + 13 + 15}{2} = 16 [cm]$ .

Zatem pole tego trójkąta jest równe:

$P_{△} = \sqrt{16 (16 - 4) (16 - 13) (16 - 15)} = \sqrt{16 \cdot 12 \cdot 3 \cdot 1} = \sqrt{16 \cdot 36} =$

$= 4 \cdot 6 = 24 [{cm}^{2}]$ .

Przykład 3

Obliczymy długość promienia okręgu opisanego na trójkąciepromienia okręgu opisanego na trójkącie równoramiennym o podstawie $8 cm$ i ramieniu długości $4 \sqrt{5} cm$ .

Rozwiązanie

Sprawdzimy jakim trójkątem jest trójkąt o podanych długościach, by poprawnie wykonać rysunek pomocniczy:

${(4 \sqrt{5})}^{2} + 8^{2} > {(4 \sqrt{5})}^{2}$ , zatem jest to trójkąt ostrokątny, środek okręgu opisanego na nim leży wewnątrz trójkąta.

$I$ sposób:

R1EjElf6D8oyO

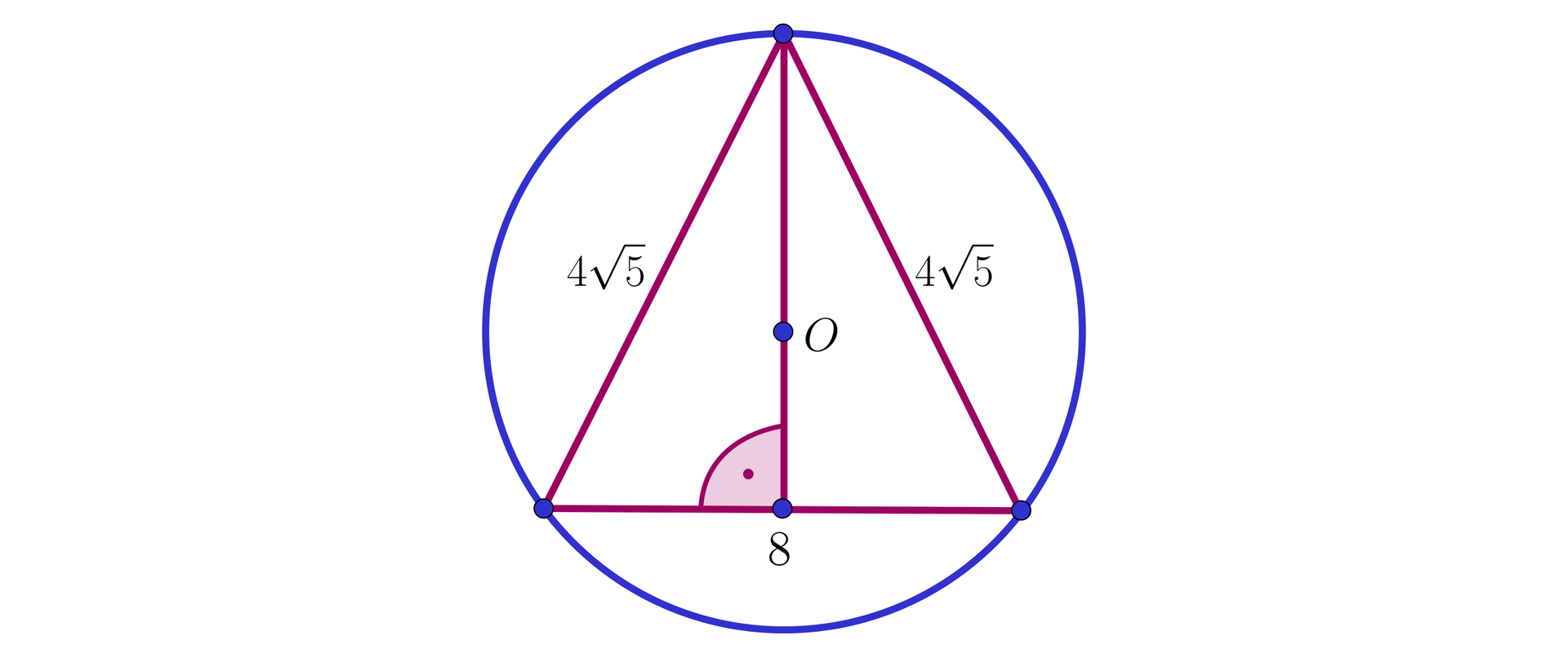
Ilustracja przedstawia trójkąt wpisany w okrąg. Środek okręgu podpisano literą O. Punk o leży na wysokości trójkąta opuszczonej na bok o długości osiem. Pozostałe boki trójkąta mają długość 45.

Korzystając z twierdzenia Pitagorasa obliczymy wysokość trójkąta opuszczoną na podstawę:

$h^{2} + 4^{2} = {(4 \sqrt{5})}^{2}$

$h^{2} + 16 = 80$

$h^{2} = 64$

$h = 8 [cm]$

Możemy już obliczyć pole tego trójkąta

$P = \frac{8 \cdot 8}{2} = 32 [{cm}^{2}]$

Przekształcając poznany wzór $P = \frac{a b c}{4 R}$ , obliczymy długość promienia okręgu opisanego na tym trójkącie

$R = \frac{a b c}{4 P}$

$R = \frac{4 \sqrt{5} \cdot 4 \sqrt{5} \cdot 8}{4 \cdot 32} = 5 [cm]$

$II$ sposób:

RgxwrX92Lnqj4

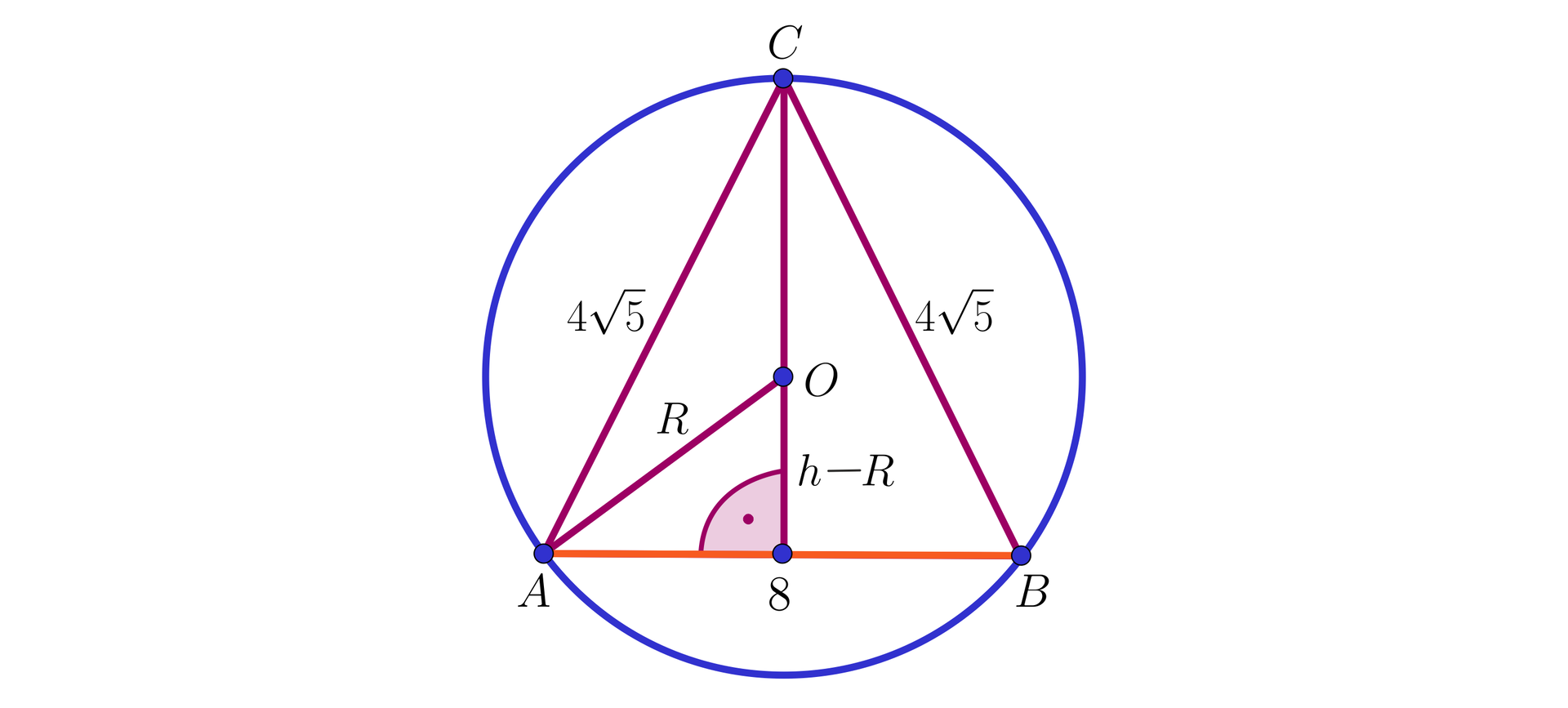
Zauważmy, że mamy trójkąt prostokątny o przyprostokątnych $h - R = 8 - R$ , $4$ oraz przeciwprostokątnej $R$ .

Stosując twierdzenie Pitagorasa otrzymujemy

${(8 - R)}^{2} + 4^{2} = R^{2}$

$64 - 16 R + R^{2} + 16 = R^{2}$

$80 = 16 R$

$R = 5 [cm]$

Przypomnimy teraz:

sinusów

Twierdzenie: sinusów

R4qo3SMIiUcUY

Ilustracja przedstawia trójkąt A B C, który został wpisany w okrąg o środku O. Odcinek BO podpisano literą R. Odcinek AB podpisano literą c. Odcinek BC podpisano literą a. Odcinek AC podpisano literą b. Kąt BAC podpisano literą alfa. Kąt CBA podpisano literą beta. Kąt EC podpisano literą gamma. Wierzchołki A C E tworzą trójkąt.

W dowolnym trójkącie stosunki długości boków do sinusów przeciwległych kątów są równe długości średnicy okręgu opisanego na tym trójkącie:

\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ} = 2 R

Przykład 4

Obliczymy długość promienia okręgu opisanego na trójkąciepromienia okręgu opisanego na trójkącie, w którym jeden z boków ma długość $10 cm$ , a przeciwległy do niego kąt ma miarę $30 °$ .

Rozwiązanie

Korzystając z twierdzenia sinusów wiemy, że stosunek długości boku do sinusa kąta leżącego naprzeciw jest równy długości średnicy okręgu opisanego na tym trójkącie, zatem

$2 R = \frac{10}{\sin 30 °} = \frac{10}{\frac{1}{2}} = 20$

Stąd $R = 10 [cm]$ .

Przykład 5

Obliczymy długość promienia okręgu opisanego na trójkąciepromienia okręgu opisanego na trójkącie o kątach $60 °$ i $75 °$ oraz boku przy tych kątach długości $12$ .

Rozwiązanie

Suma kątów wewnętrznych w trójkącie wynosi $180 °$ .

Zatem miara trzeciego kąta wynosi $180 ° - 60 ° - 75 ° = 45 °$ .

Naprzeciw kąta o mierze $45 °$ leży bok długości $12$ .

Zatem: $2 R = \frac{12}{\sin 45 °} = \frac{12}{\frac{\sqrt{2}}{2}} = 12 \sqrt{2}$

Z powyższego wynika, że $R = 6 \sqrt{2}$ .

Przykład 6

Dwa boki trójkąta wpisanego w okrąg o promieniu długości $R = 6 \sqrt{2}$ mają długości $a = 6 \sqrt{2}$ i $b = 9 \sqrt{2}$ . Obliczymy długość trzeciego boku tego trójkąta.

Rozwiązanie

Niech $α$ będzie kątem leżącym naprzeciw boku $a$ , zaś $c$ – długością szukanego boku.

R1BwP0RYLeXpr

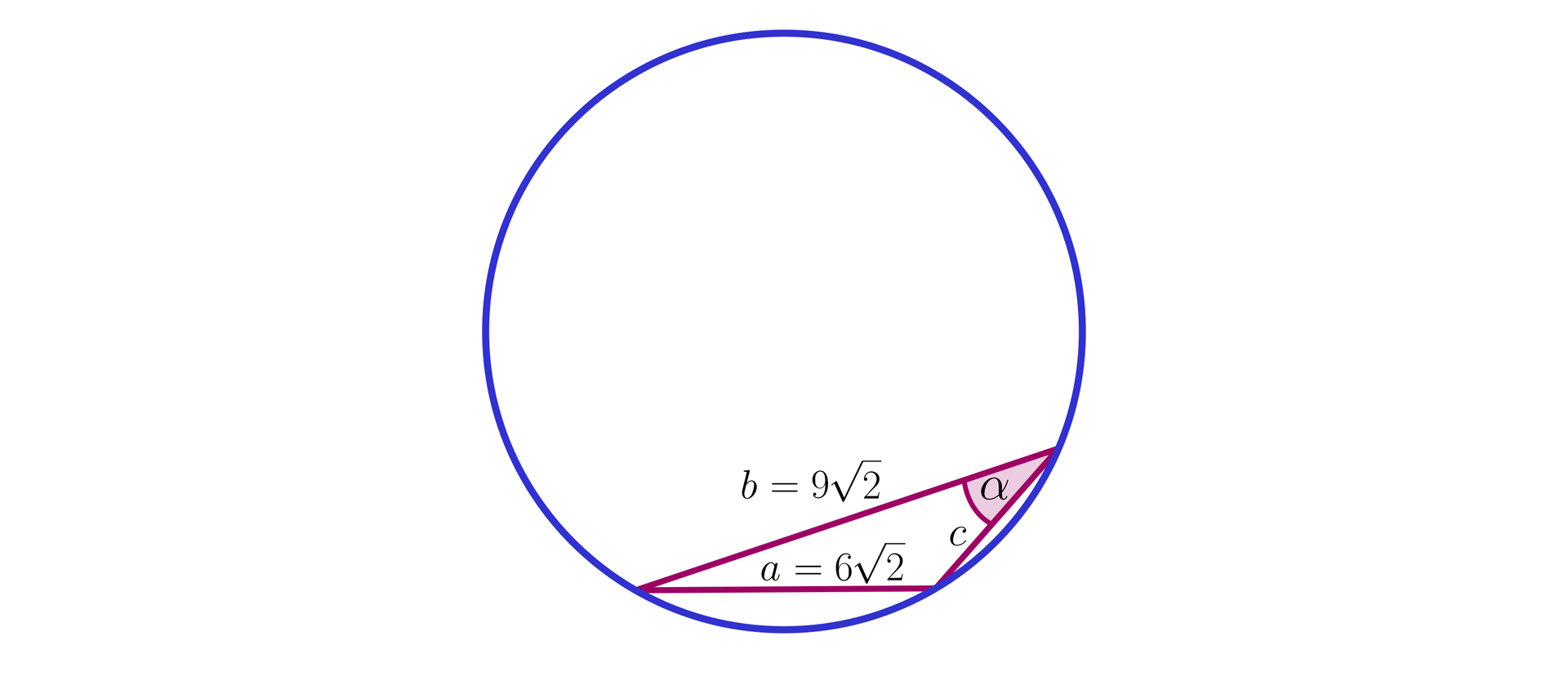
Ilustracja przedstawia trójkąt rozwartokątny wpisany w okrąg. Jeden z kątów trójkąta podpisano literą alfa. Jeden z boków leżący przy tym kącie podpisano literą c, a drugi podpisano b=92, trzeci bok podpisano a=62.

Z twierdzenia sinusów:

$\frac{6 \sqrt{2}}{\sin α} = 12 \sqrt{2}$ .

Stąd: $\sin α = \frac{1}{2}$ , co daje: $α = 30 °$ .

Z twierdzenia cosinusów:

${(6 \sqrt{2})}^{2} = c^{2} + {(9 \sqrt{2})}^{2} - 2 \cdot c \cdot 9 \sqrt{2} \cdot \cos 30 °$

$72 = c^{2} + 162 - 2 \cdot c \cdot 9 \sqrt{2} \cdot \frac{\sqrt{3}}{2}$

$c^{2} - 9 \sqrt{6} c + 90 = 0$

$∆ = 486 - 360 = 126$

$\sqrt{∆} = 3 \sqrt{14}$

$c_{1} = \frac{9 \sqrt{6} - 3 \sqrt{14}}{2}$ lub $c_{2} = \frac{9 \sqrt{6} + 3 \sqrt{14}}{2}$

Przykład 7

W trójkącie $A B C$ kąt przy wierzchołku $B$ jest ostry. Długość promienia okręgu opisanego na tym trójkącie jest równa $10$ oraz $|A C| = 12$ , $|A B| = 24$ . Na boku $B C$ wybrano taki punkt D, że $|B D| = 4$ . Obliczymy długość odcinka $A D$ .

Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku:

R1Scl7nL71zm8

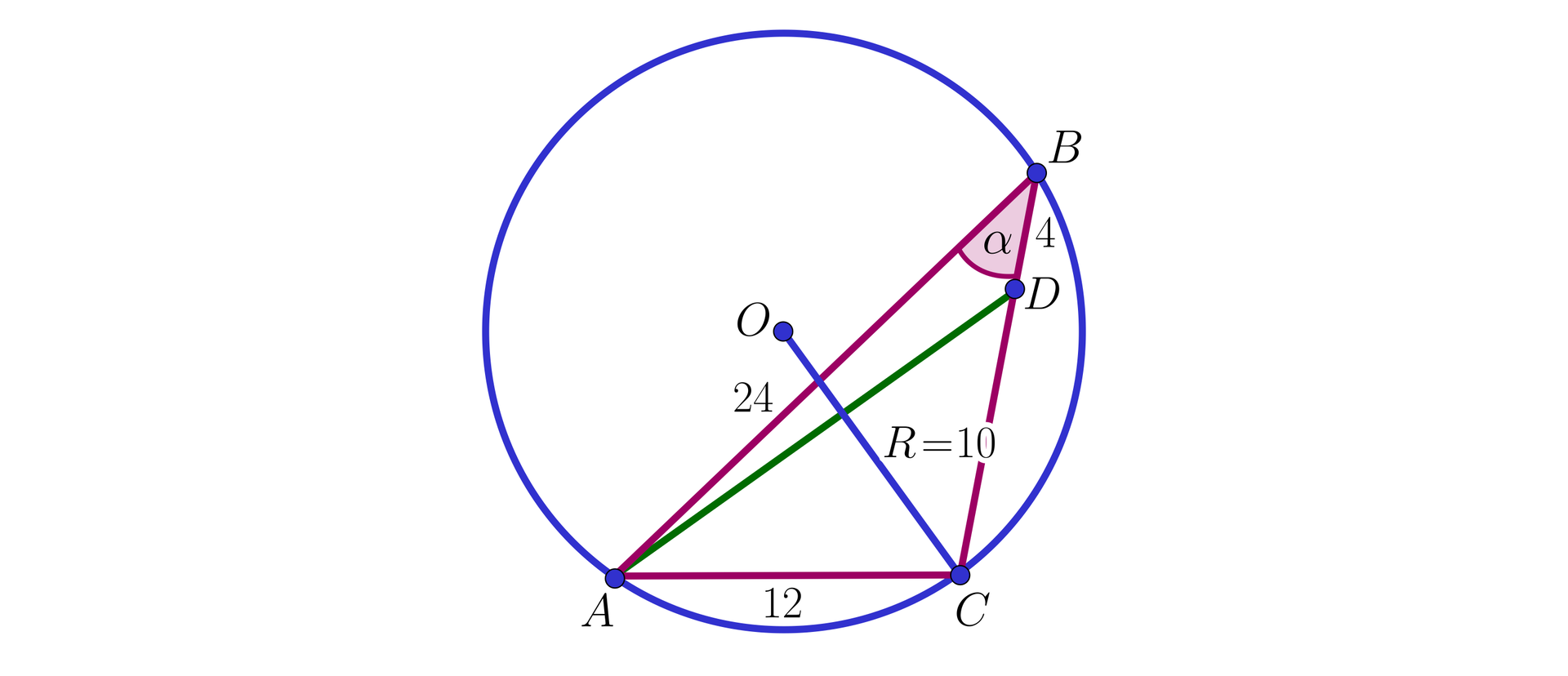
Ilustracja przedstawia trójkąt A B C, który został wpisany w okrąg o środku O. Bok AC ma długość 12, odcinek AB ma długość dwadzieścia cztery. Na odcinku BC zaznaczono punkt D, odcinek BD ma długość cztery. Odcinek OC podpisano R=10. W trójkącie zaznaczono odcinek AD. Kąt CBA podpisano literą alfa.

Zastosujemy twierdzenie sinusów w trójkącie $A B C$ :

$\frac{12}{\sin α} = 2 R$

Zatem: $\sin α = \frac{12}{20} = 0, 6$ .

Wyznaczymy wartość cosinusa kąta $α$ :

$\sin^{2} α + \cos^{2} α = 1$

${(0, 6)}^{2} + \cos^{2} α = 1$

$\cos^{2} α = 0, 64$

$\cos α = 0, 8$ lub $\cos α = - 0, 8$ .

Ponieważ $α \in (0 °; 90 °)$ , to $\cos α = 0, 8$ .

Stosujemy twierdzenie cosinusów do trójkąta $A B D$ :

${|A D|}^{2} = {|A B|}^{2} + {|B D|}^{2} - 2 \cdot |A B| \cdot |B D| \cdot \cos α$

${|A D|}^{2} = 24^{2} + 4^{2} - 2 \cdot 24 \cdot 4 \cdot 0, 8$

${|A D|}^{2} = 438, 4$

$|A D| = \sqrt{438, 4}$

Ważne!

Jeżeli nie zostanie podane, że jest inaczej, przyjmujemy, że boki trójkąta o długości: $a$ , $b$ , $c$ leżą odpowiednio naprzeciw kątów: $α$ , $β$ , $γ$ .

Słownik

trójkąt wpisany w okrąg

trójkąt jest wpisany w okrąg, gdy wszystkie jego wierzchołki leżą na okręgu; mówimy wówczas, że okrąg jest opisany na trójkącie; promień takiego okręgu oznaczamy przez $R$

promień okręgu opisanego na trójkącie

jest to długość odcinka łączącego środek tego okręgu z dowolnym wierzchołkiem trójkąta, oznaczamy go przez $R$

Wprowadzenie

Symulacja interaktywna

Słownik