Symulacja interaktywna
Polecenie 1
Prześledź zależność między długością boku a sinusem kąta leżącego naprzeciw tego boku, a następnie wykonaj poniższe polecenia. Zmieniając położenie wierzchołków trójkąta w poniższej symulacji interaktywnej samodzielnie decydujesz, jakiemu trójkątowi się przyglądasz.
Zapoznaj się z poniższym opisem symulacji. Prześledź zależność między długością boku a sinusem kąta leżącego naprzeciw tego boku, a następnie wykonaj poniższe polecenia.
,
,
,
,
,
,
,
oraz
.
Następnie liniami przerywanymi narysowano symetralne boków trójkąta. Symetralne boków trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu opisanego na trójkącie. Odcinki AS, BS oraz CS podpisano literą R, przy czym . Zauważmy, że
,
oraz
.
Przypomnijmy również, że . Zmieniając położenie punktów A B oraz C otrzymujemy:
,
,
,
,
,
,
,
oraz
.
Długość promienia wynosi ,
,
oraz
.
Dla trójkąta A B C o parametrach:
,
,
,
,
,
,
,
oraz
.
Otrzymujemy długość promienia ,
,
oraz
.
Możemy zauważyć, że zachodzi równość:
.
Zatem możemy sformułować wniosek w postaci twierdzenia sinusów: Długość promienia opisanego na trójkącie jest równa długości boku przez podwojony sinus kąta leżącego naprzeciw tego boku
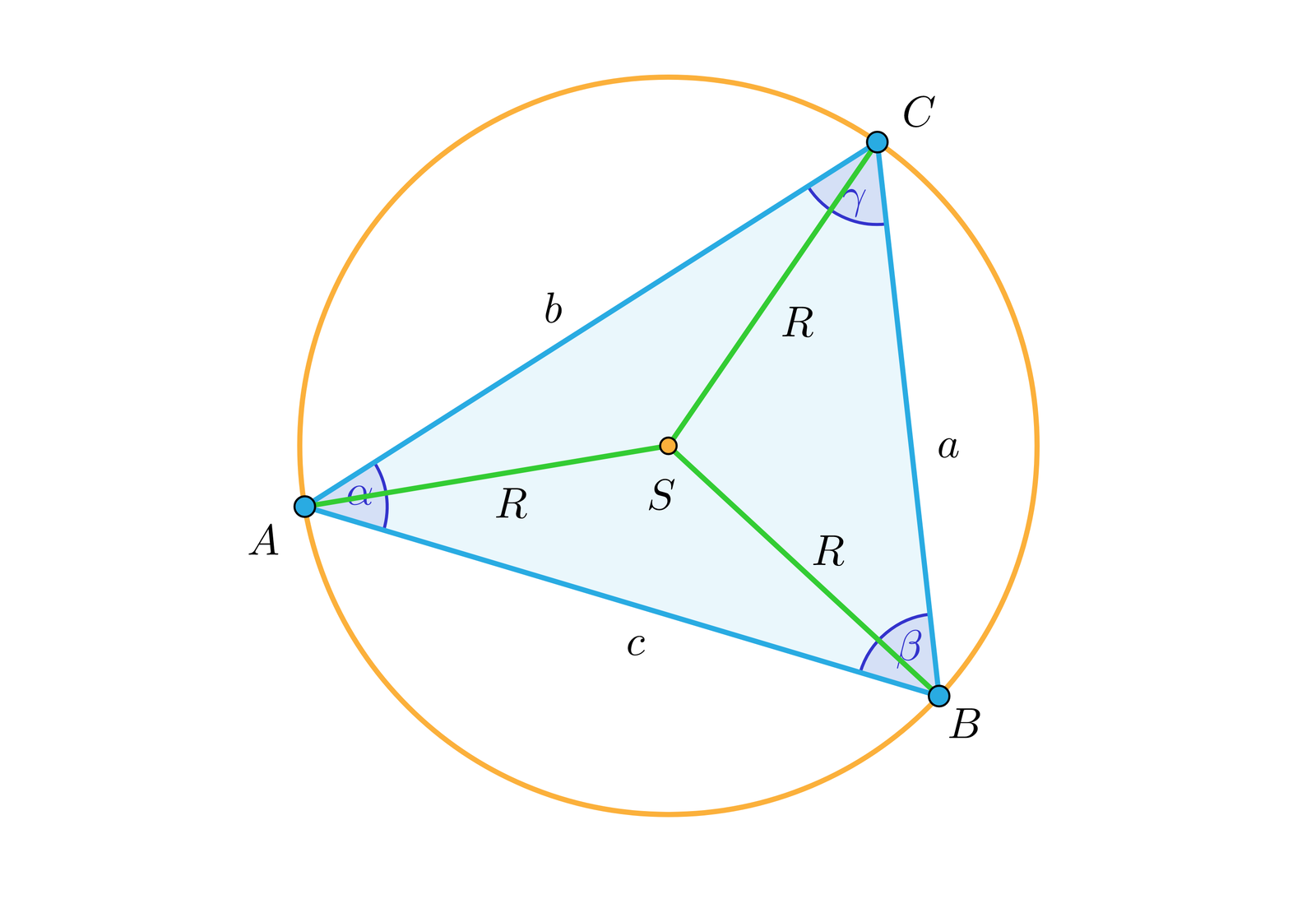
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DGXNQz7l4
Polecenie 2
Oblicz długość promienia okręgu opisanego na trójkącie , jeśli , .
Polecenie 3
Oblicz miary pozostałych kątów trójkąta , jeżeli , , .
Polecenie 4
W trójkącie , wpisanym w okrąg o promieniu , dane są miary dwóch kątów: , . Oblicz obwód tego trójkąta.