Animacja

Polecenie 1

Zapoznaj się z animacją, następnie spróbuj rozwiązać zadania zamieszczone w poleceniach.

Re8ftUNtSfqHD

Film dostępny pod adresem https://zpe.gov.pl/a/DeLUkx26V

Film nawiązujący do treści materiału dotyczącej równań i nierówności.

Polecenie 2

Motorowerzysta pokonuje drogę z miasta $A$ do miasta $B$ ze średnią prędkością $V_{1}$ , natomiast pokonując drogę powrotną z $B$ do $A$ (tą samą trasą), porusza się z prędkością $V_{2}$ . Aby obliczyć średnią prędkość $V_{śr}$ motorowerzysty na trasie z $A$ do $B$ i z powrotem należy posłużyć się średnią harmoniczną, która jest statystyczną miarą położenia stosowaną wtedy, gdy dane przedstawione są w postaci względnej, tzn. w przeliczeniu na stałą jednostkę innej zmiennej np. prędkość wyrażona w $[\frac{km}{h}]$ . Średnią harmoniczną liczb dodatnich definiujemy jako odwrotność średniej arytmetycznej z odwrotności danych. Poniżej zapisano wzór na prędkość średnią motorowerzysty w opisanej sytuacji z zastosowaniem definicji średniej harmonicznej dla prędkości $V_{1}$ oraz $V_{2}$ :

$V_{ś r} = \frac{1}{\frac{\frac{1}{V_{1}} + \frac{1}{V_{2}}}{2}}$

Zapisz powyższy wzór w najprostszej postaci.
Wiedząc, że motorowerzysta poruszał się z $A$ do $B$ ze średnią prędkością $40 \frac{km}{h}$ , oblicz z jaką minimalną prędkością powinien wracać, aby na całej trasie tam i z powrotem osiągnąć średnią prędkość przynajmniej $48 \frac{km}{h}$ .

$V_{śr} = \frac{1}{\frac{\frac{1}{v_{1}} + \frac{1}{v_{2}}}{2}}$
$V_{śr} = \frac{1}{\frac{V_{1} + V_{2}}{\frac{V_{1} V_{2}}{2}}} = \frac{2}{\frac{V_{1} + V_{2}}{V_{1} \cdot V_{2}}} = \frac{2 V_{1} \cdot V_{2}}{V_{1} + V_{2}}$
$V_{śr} = \frac{2 V_{1} \cdot V_{2}}{V_{1} + V_{2}}$
$V_{1} = 40 \frac{km}{h}$
$V_{2} = ?$
$V_{śr} ⩾ 48 \frac{km}{h}$
$V_{śr} = \frac{2 V_{1} \cdot V_{2}}{V_{1} + V_{2}}$
Z warunków zadania mamy:
$\frac{2 V_{1} \cdot V_{2}}{V_{1} + V_{2}} ⩾ 48$
Po podstawieniu danych otrzymujemy:
$\frac{2 \cdot 40 \cdot V_{2}}{40 + V_{2}} ⩾ 48 | \cdot (40 + V_{2})$
Wykonujemy przekształcenie równoważne nierówności polegające na obustronnym jej pomnożeniu przez wyrażenie stale dodatnie, czego efektem jest nierówność równoważna:
$80 V_{2} ⩾ 48 (40 + V_{2}) | : 16$
$5 V_{2} ⩾ 120 + 3 V_{2} | - 3 V_{2}$
$2 V_{2} ⩾ 120 | : 2$
$V_{2} ⩾ 60$
Odpowiedź: Motorowerzysta powinien wracać z minimalną prędkością $60 \frac{km}{h}$ .

Polecenie 3

Rezystancja, czyli opór elektryczny, to wielkość charakteryzująca relację między napięciem a natężeniem prądu elektrycznego w obwodach prądu stałego (źródło: Wikipedia).

Jak wiesz z fizyki układy rezystorów (oporników) mogą powstawać w połączeniach szeregowych lub równoległych. W przypadku tych ostatnich połączeń opór zastępczy dwóch i więcej rezystorów wyraża się wzorem:

RXwthWqOCok9y

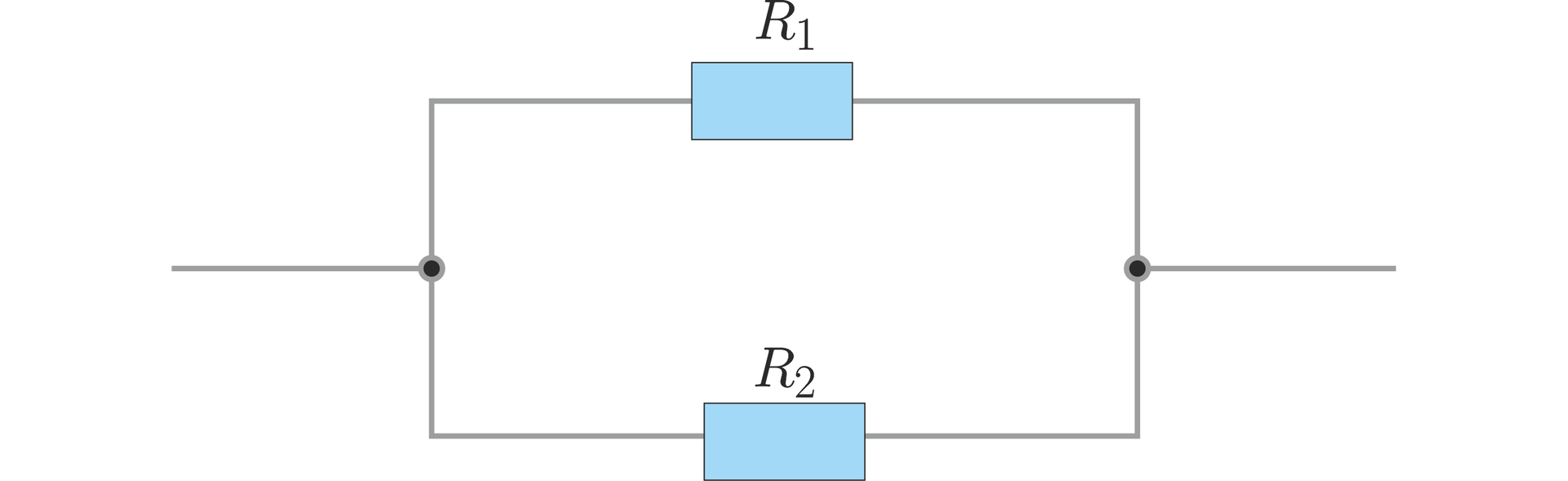
Rysunek przedstawia obwód elektryczny w kształcie prostokąta z dwoma rezystorami. Do środka lewego boku prostokąta dochodzi pionowa linia, na środku górnego i dolnego boku prostokąta leżą rezystory odpowiednio R indeks dolny 1 oraz R indeks dolny 2. Z środka prawego boku odchodzi pionowa linia.

$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$

R1MsvWXAciCJq

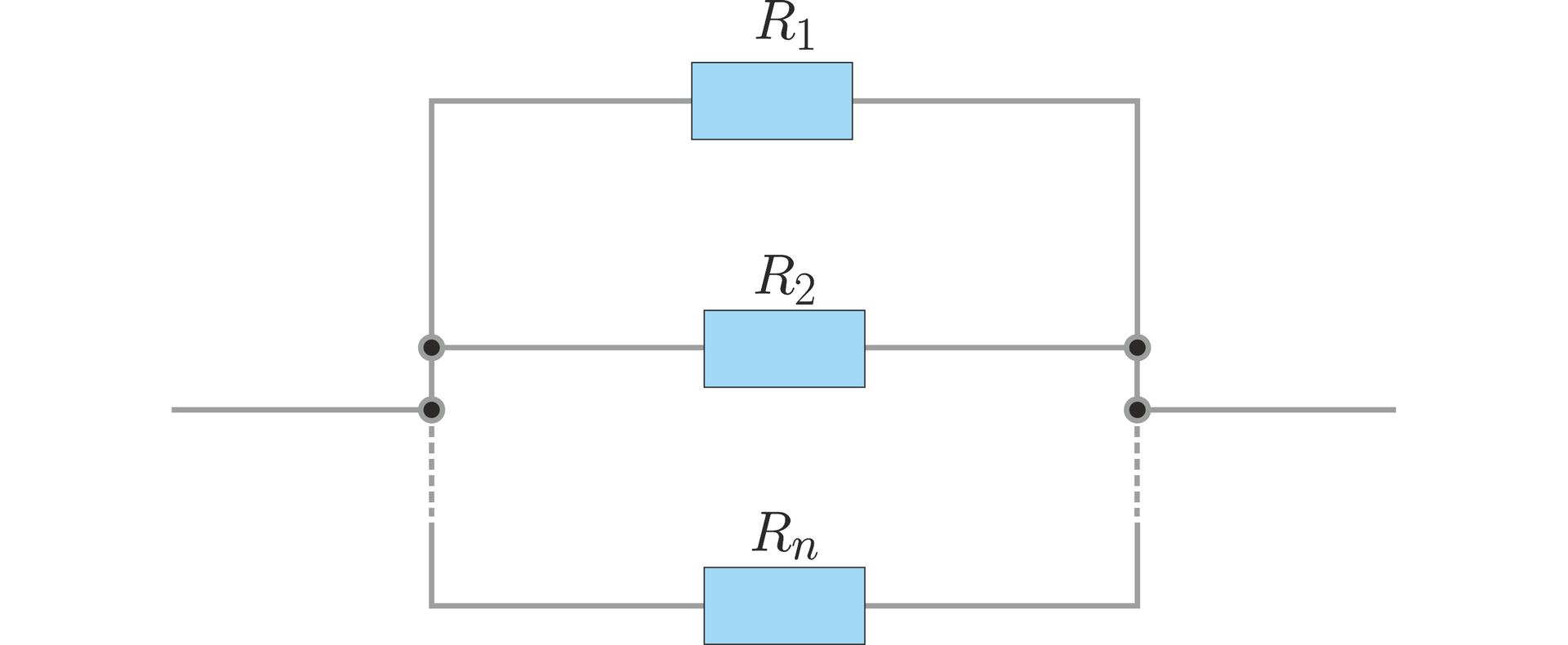
Rysunek przedstawia obwód elektryczny w kształcie prostokąta z n rezystorami. Do środka lewego boku prostokąta dochodzi pionowa linia, na środku górnego i dolnego boku prostokąta leżą rezystory odpowiednio R indeks dolny 1 oraz R indeks dolny n. Wewnątrz prostokąta poprowadzono odcinek łączący prawy bok z lewym, który jest równoległy do górnego i dolnego boku. Na środku odcinka oznaczony jest rezystor R z indeksem 2. Dolna połowa lewego i prawego boku prostokąta jest zaznaczona przerywaną linią sugerującą, że wewnątrz prostokąta znajduje się więcej takich odcinków wyglądających analogicznie jak ten który zawiera rezystor R indeks dolny 2. Z środka prawego boku odchodzi pionowa linia.

$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \dots + \frac{1}{R_{n}}$

Mając do dyspozycji oporniki o rezystancji $R_{1} = 50 Ω$ (omów) oraz $R_{2} = 60 Ω$ , dobierz maksymalną rezystancję trzeciego opornika ( $R_{3}$ ) tak, aby opór zastępczy $R$ wyrażony liczbą całkowitą był nie większy niż $21 Ω$ .

$R_{1} = 50 Ω$ , $R_{2} = 60 Ω$ , $R_{3} = ?, R ⩽ 21 Ω$

$\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}}$

Z powyższego wzoru wyprowadzimy wielkość $R$ , wykonując przekształcenia równoważne:

$\frac{1}{R} = \frac{R_{2} R_{3} + R_{1} R_{3} + R_{1} R_{2}}{R_{1} R_{2} R_{3}}$

$R = \frac{R_{1} R_{2} R_{3}}{R_{2} R_{3} + R_{1} R_{3} + R_{1} R_{2}}$

Uwzględniając warunki zadania oraz dane otrzymujemy nierówność (pomijamy zgodne jednostki):

$\frac{50 \cdot 60 R_{3}}{60 R_{3} + 50 R_{3} + 50 \cdot 60} ⩽ 21$

$\frac{3000 R_{3}}{110 R_{3} + 3000} ⩽ 21 | \cdot (110 R_{3} + 3000)$

Mnożymy obie strony nierówności przez wyrażenie stale dodatnie i otrzymujemy:

$3000 R_{3} ⩽ 21 (110 R_{3} + 3000)$

$3000 R_{3} ⩽ 210 (11 R_{3} + 300) | : 30$

$100 R_{3} ⩽ 7 (11 R_{3} + 300)$

$100 R_{3} ⩽ 77 R_{3} + 2100$

$23 R_{3} ⩽ 2100 | : 23$

$R_{3} ⩽ 91, 30$

Ponieważ wymagamy aby szukana wartość była całkowita, zatem rezystancja $R_{3}$ może wynosić maksymalnie $91 Ω$ .

$R_{3} = 91 Ω$

Przeczytaj

Sprawdź się