Aplet
Uruchom aplet. Ustal położenie wierzchołków czworokąta wpisanego w okrąg, a następnie wybierz polecenie „Rozcinanie czworokąta”. Odczytaj miary kątów wewnętrznych trójkątów powstałych w wyniku triangulacji. Sprawdź, że spełnione są warunki twierdzenia o czworokącie wpisanym w okrąg.
Zapoznaj się z poniższym opisem apletu przybliżającym zagadnienie rozcinania czworokąta.
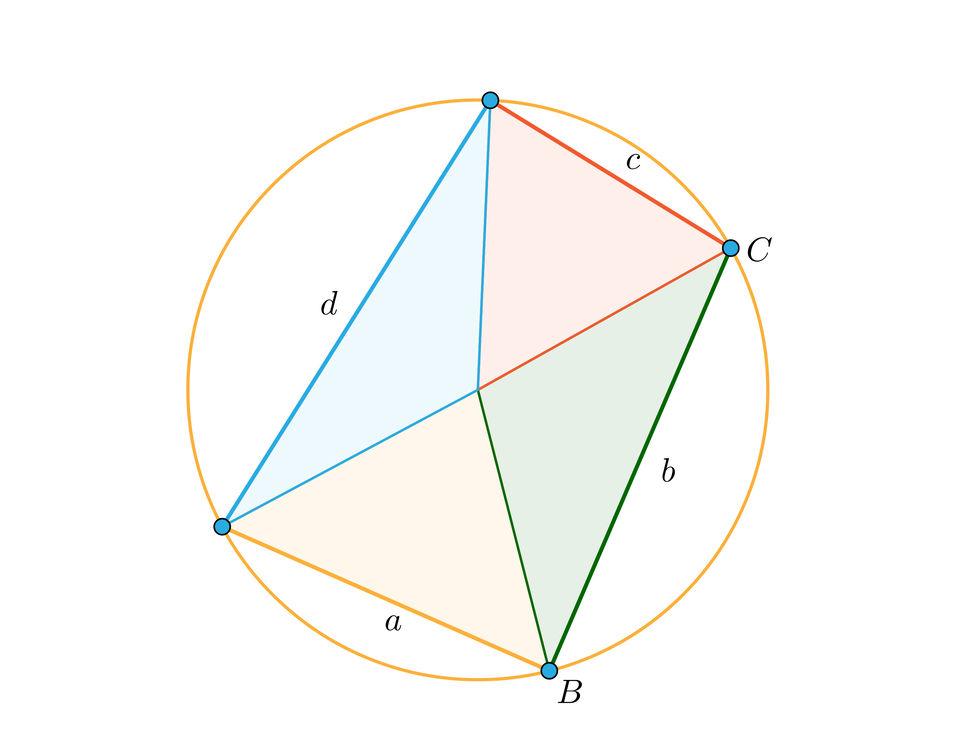
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfD0okMv3
Miary kątów wewnętrznych trójkątów, na jakie rozcięto czworokąt wpisany w okrąg, a którego bokami są promienie okręgu opisanego na tym czworokącie, poprowadzone do jego wierzchołków, mają miary odpowiednio równe: , , , . Oblicz miary kątów wewnętrznych tego czworokąta, przy różnych położeniach tych trójkątów.
Boki czworokąta wpisanego w okrąg mają długości , , , . Oblicz długości przekątnych tego czworokąta i czworokąta wpisanego w ten sam okrąg, którego boki mają długości , , , .