Przeczytaj
Bryły platońskie
Bryły platońskie (wielościanywielościany foremne) to bryły, których wszystkie ściany są przystającymi wielokątamiprzystającymi wielokątami foremnymi i w których z każdego wierzchołka wychodzi tyle samo krawędzi.
Z trójkątów równobocznych złożyć można trzy bryły idealne:
tetraedr (czworościan foremny),
oktaedr (ośmiościan foremny),
ikosaedr (dwudziestościan foremny).
Czwartą bryłę reprezentuje heksaedr (sześcian), którego każda ściana da się podzielić na dwa trójkąty, jest więc też zbudowany z trójkątów.
Istnieje wreszcie piąta bryła foremna - dodekaedr, zbudowana z pięciokątów regularnych, którą Platon uznał za zespolenie całości, bryłę łączącą wszystkie elementy.
tetraedrem opis alternatywny
trójkąty
Ilustracja przedstawia pięć brył. Pierwszą z nich jest ostrosłup o podstawie trójkąta, jest on podpisany czworościan foremny, czyli inaczej
tetraedrem, jego siatka składa się z czterech trójkątów. Pod ilustracją siatki zapisano:
[trójkąty]
.
Drugą figurą jest sześcian, czyli inaczej prostopadłościan foremny, inaczej:
heksaedr jego siatka składa się z sześciu kwadratów. Pod ilustracją siatki zapisano:
[kwadraty]
.
Kolejna figura to ośmiościan foremny, czyli oktaedr, jego siatka składa się z ośmiu trójkątów. Pod ilustracją siatki zapisano:
[trójkąty]
.
Następna figura to dwunastościan foremny, dodekaedr jego siatka składa się z 12 pięciokątów, które wyglądają jak dwa połączone ze sobą pięciolistne kwiaty. Pod ilustracją siatki zapisano:
[pięciokąty]
.
Ostatnią bryłą jest dwudziestościan foremny ikosaedr, jego siatka składa się z 20 trójkątów. Pod ilustracją siatki zapisano:
[trójkąty]
.
Dlaczego tylko pięć brył?
Pitagoras udowodnił, że płaszczyzna dookoła punktu może być zapełniona jednolicie tylko trzema rodzajami wielokątów foremnych: trójkątami, kwadratami albo pięciokątami. Żeby powstało naroże, potrzebne są co najmniej trzy ściany a suma kątów płaskich w wierzchołku musi być mniejsza od kąta pełnego. Wszystkie ściany w przypadku brył platońskich są jednakowe. Zatem jeśli wielokąty foremne tego samego rodzaju mają utworzyć naroże, to takich kombinacji jest właśnie pięć.
Omówmy po kolei wszystkie bryły.
Czworościan foremny
Czworościan foremny to taki ostrosłup, który ma w podstawie oraz ścianach bocznych trójkąty równoboczne.
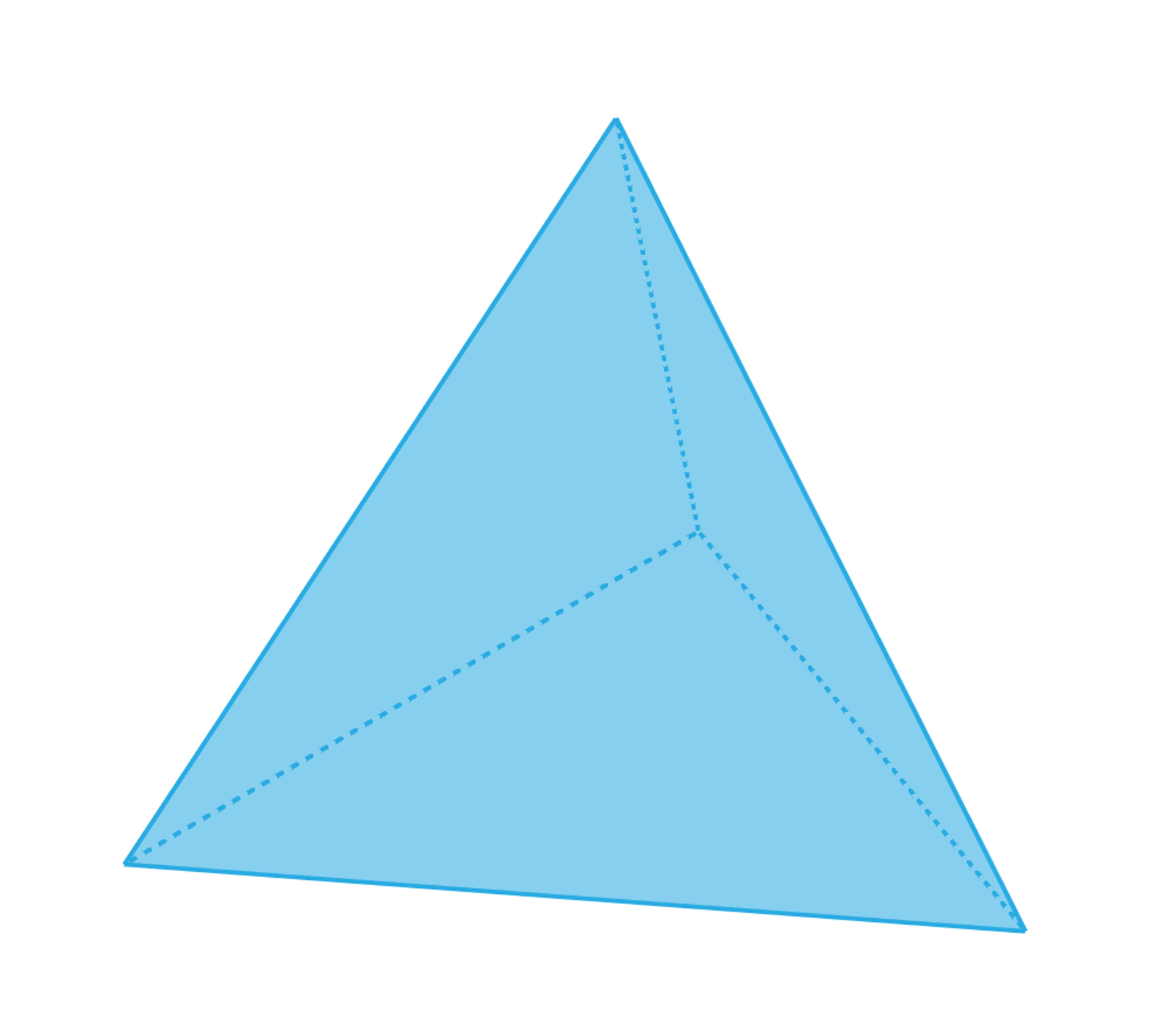
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfKmqFDm0
Wzory:
Wzór na pole powierzchni czworościanu foremnego
Wzór na objętość czworościanu foremnego
Wzór na wysokość czworościanu foremnego:
Wzór na wysokość ściany bocznej czworościanu foremnego
Sześcian
Sześcian to graniastosłup, który ma sześć ścian będących przystającymi kwadratami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfKmqFDm0
Wzory:
Wzór na pole powierzchni całkowitej sześcianu
Wzór na objętość sześcianu
Ośmiościan foremny
Ośmiościan foremny ma osiem ścian będących trójkątami równobocznymi.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfKmqFDm0
Wzory:
Wzór na pole powierzchni całkowitej
Wzór na objętość
Dwunastościan foremny
Dwunastościan foremny ma dwanaście ścian będących pięciokątami foremnymi.
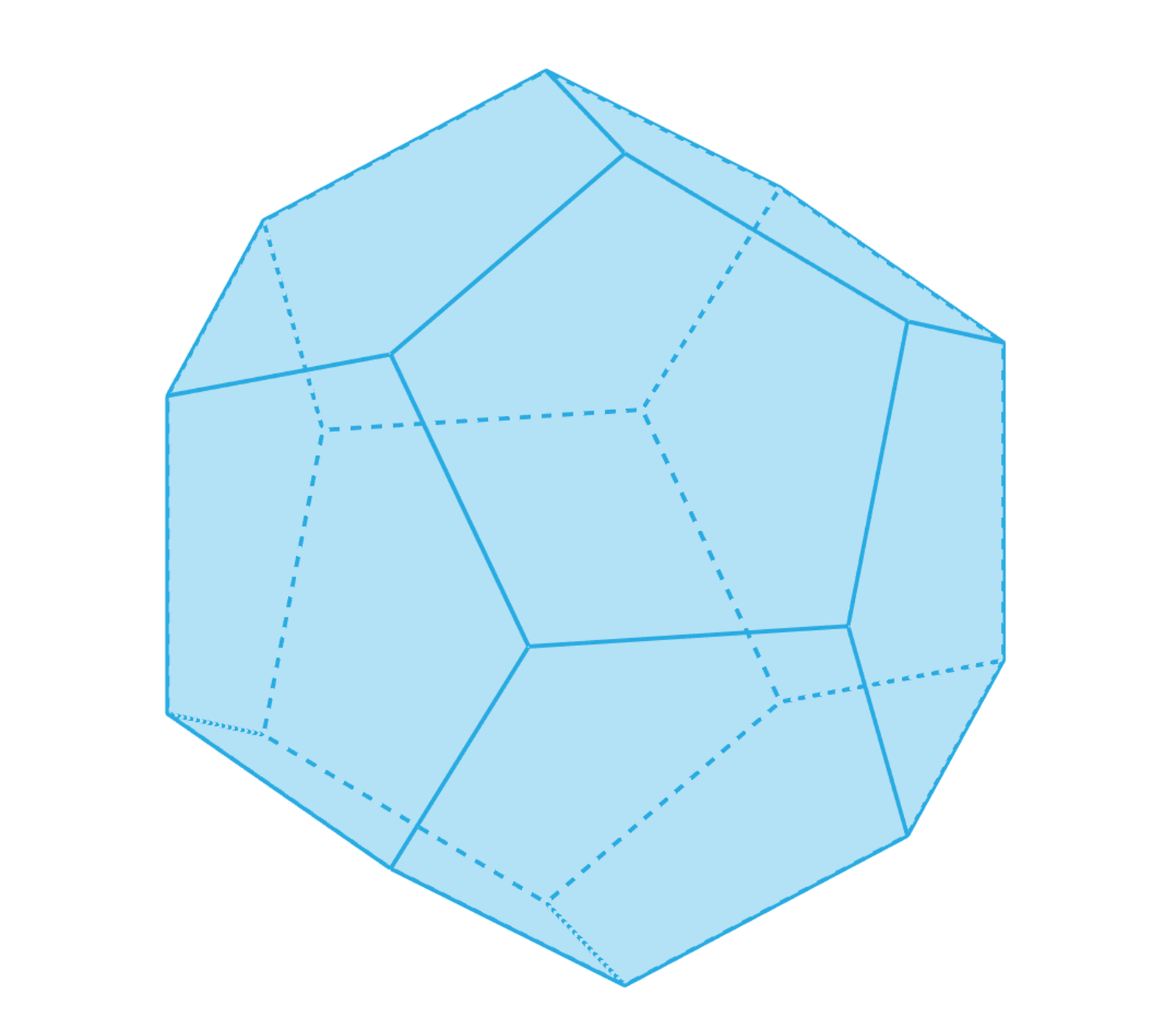
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfKmqFDm0
Siatka dwunastościanu foremnego

Wzory:
Wzór na pole powierzchni całkowitej
Wzór na objętość
Dwudziestościan foremny
Dwudziestościan foremny ma dwadzieścia ścian będących trójkątami równobocznymi.
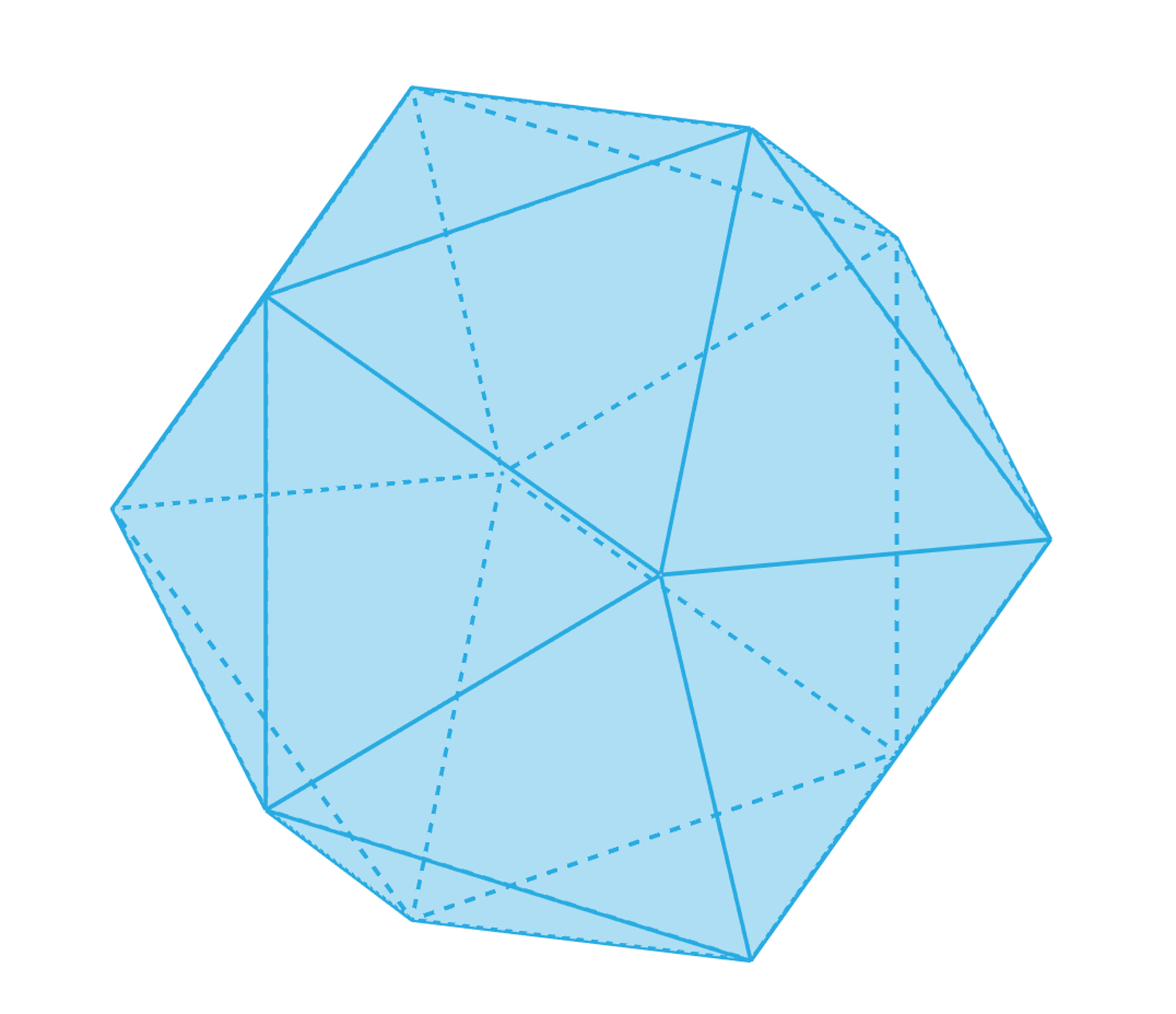
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DfKmqFDm0
Siatka dwudziestościanu foremnego
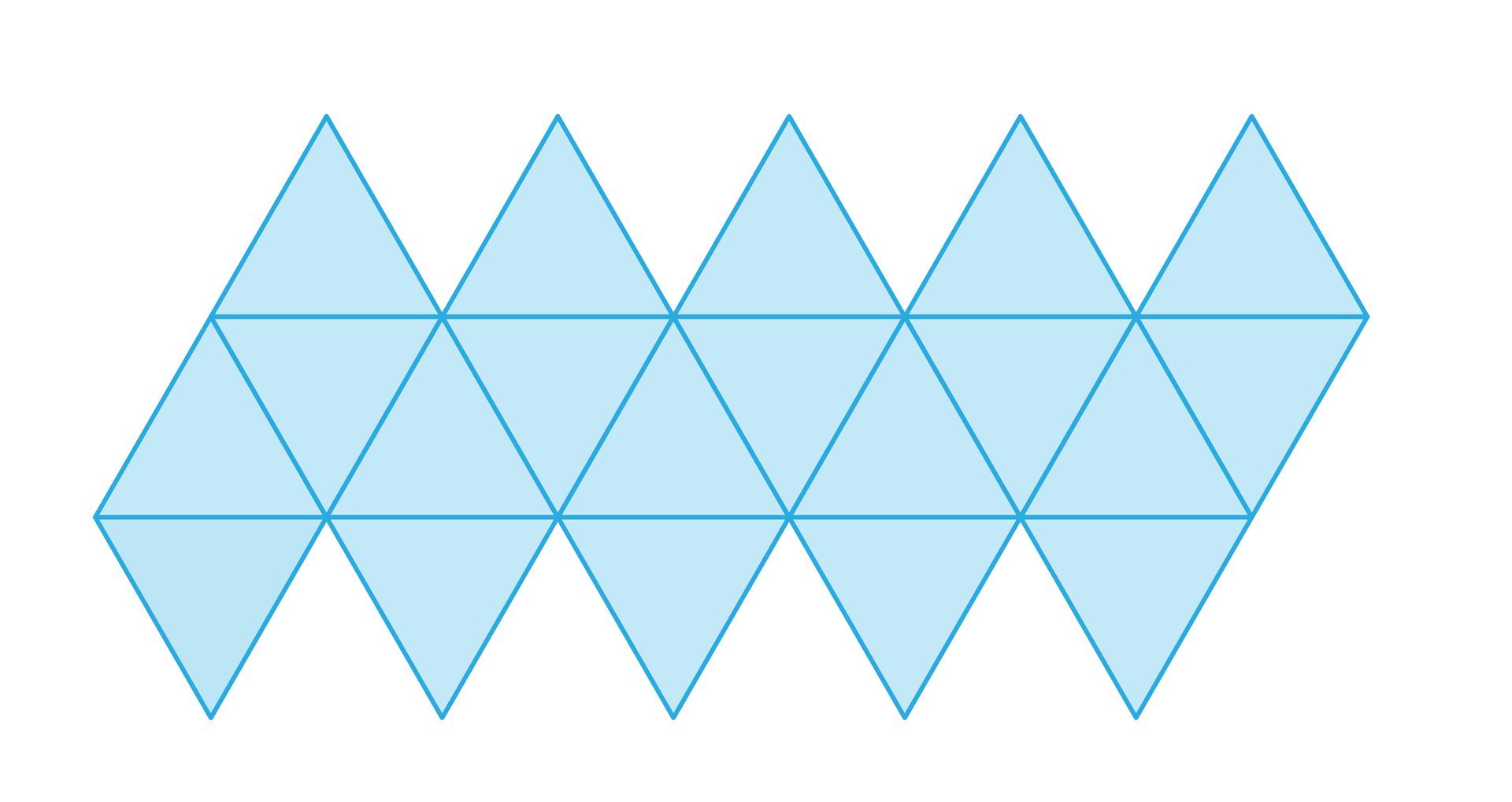
Wzory:
Wzór na pole powierzchni całkowitej
Wzór na objętość
Uzupełnijmy w tabeli dane dotyczące wielościanów foremnych. Sprawdźmy, czy dla każdego z tych wielościanów spełniony jest wzór Eulera: , gdzie oznacza liczbę ścian, - liczbę krawędzi, - liczbę wierzchołków.
Wielościan foremny | Liczba ścian | Liczba krawędzi | Liczba wierzchołków |
|---|---|---|---|
Czworościan | |||
Sześcian | |||
Ośmiościan | |||
Dwunastościan | |||
Dwudziestościan |
Zobacz rozwiązanieZobacz rozwiązanie
Sprawdźmy wzór Eulera dla każdej bryły z osobna.
Czworościan: .
Sześcian: .
Ośmiościan: .
Dwunastościan: .
Dwudziestościan: .
Zatem wzór Eulera zachodzi dla każdej bryły platońskiej.
Pole powierzchni dwunastościanu foremnego jest równe . Obliczmy sumę długości wszystkich krawędzi tego wielościanu.
Rozwiązanie
Suma długości krawędzi wynosi więc:
.
Stosunek długości krawędzi dwudziestościanu foremnego do długości krawędzi dwunastościanu foremnego jest równy . Obliczmy, który z wielościanów ma większą objętość?
Rozwiązanie
Niech – długość krawędzi dwudziestościanu foremnego, – długość krawędzi dwunastościanu foremnego.
Wówczas , czyli .
Zatem objętość dwudziestościanu foremnego wynosi:
.
Dwunastościan foremny ma objętość równą:
.
Porównajmy te dwie objętości:
.
Objętość dwudziestościanu foremnego jest większa od objętości dwunastościanu foremnego.
Przekątna sześcianu jest o dłuższa od przekątnej ściany tego sześcianu. Obliczmy długość krawędzi i objętość sześcianu.
Rozwiązanie
Oznaczmy jako długość krawędzi sześcianu. Wówczas przekątna ściany ma długość , a przekątna sześcianu - . Powstaje więc równanie:
.
Usuńmy niewymierność z mianownika:
.
Obliczmy objętość naszego sześcianu:
.
Obliczmy stosunek objętości przedstawionego na rysunku czworościanu foremnego do opisanego na nim sześcianu.
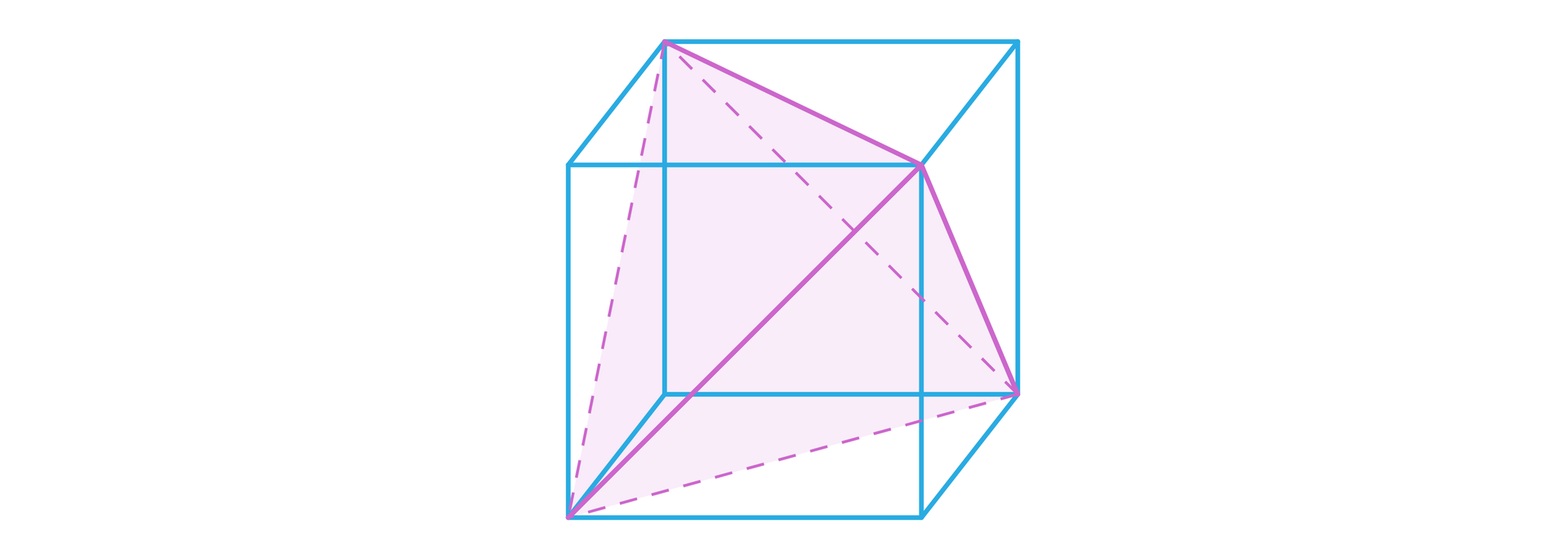
Rozwiązanie
Oznaczmy jako długość krawędzi sześcianu. Wówczas długość krawędzi czworościanu ma długość (przekątna ściany sześcianu).
Objętość czworościanu wynosi więc:
.
Objętość sześcianu wynosi . Zatem stosunek objętości czworościanu foremnego do opisanego na nim sześcianu wynosi .
Słownik
bryła geometryczna ograniczona przez tak zwaną powierzchnię wielościenną, czyli powierzchnię utworzoną z wielokątów o rozłącznych wnętrzach i każdym boku wspólnym dla dwóch wielokątów. Każdy wielościan utworzony jest ze ścian – wielokątów, które razem tworzą powierzchnię wielościanu
wszystkie figury, które mają taką samą liczbą boków o takiej samej długości oraz kąty między tymi bokami mające takie same wartości; figury przystające mają więc takie samo pole powierzchni i idealnie się na siebie nakładają