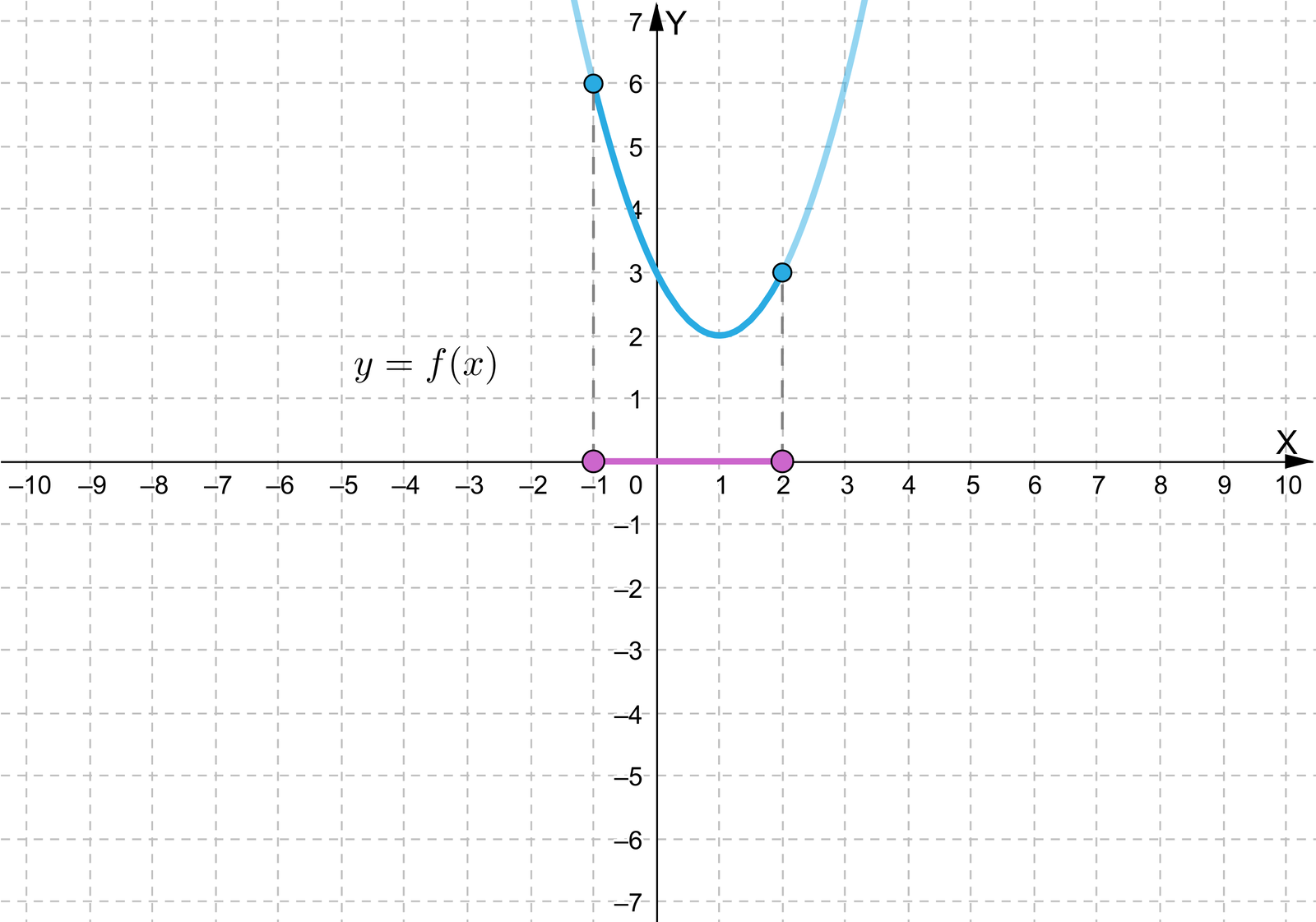
a) Obliczamy wartość pierwszej współrzędnej wierzchołka paraboli, będącej wykresem funkcji kwadratowej :
.
Ponieważ oraz , zatem funkcja przyjmuje wartość największą w wierzchołku paraboli, będącej wykresem funkcji , a wartość najmniejszą w jednym z końców podanego przedziału.
Zatem:
,
,
.
Ponieważ , to wartość najmniejsza funkcji wynosi , a wartość największa funkcji wynosi .
b) Obliczamy wartość pierwszej współrzędnej wierzchołka paraboli, będącej wykresem funkcji kwadratowej :
.
Zauważmy, że , zatem obliczamy tylko wartości funkcji na końcach podanego przedziału.
Zatem:
,
.
Ponieważ , to wartość najmniejsza funkcji wynosi , a wartość największa funkcji wynosi .