Aplet
Polecenie 1
Przeanalizuj aplet dotyczący przesunięcia wykresu funkcji logarytmicznej wzdłuż osi odciętych oraz osi rzędnych układu współrzędnych. Zwróć uwagę, które z własności wykresu oraz funkcji logarytmicznej ulegają zmianie po przesunięciu.
Rozwiąż test składający się czterech pytań jednokrotnego wyboru i z dwóch pytań wielokrotnego wyboru. Wyciągnij wnioski, jak wzór funkcji logarytmicznej przekłada się na jej wykres i jego położenie oraz przesunięcie.
Z czym jest równoznaczne przekształcenie tej funkcji do postaci ? Możliwe odpowiedzi: 1. Z przesunięciem wykresu funkcji o wektor ., 2. Z przesunięciem wykresu funkcji o wektor ., 3. Z przesunięciem wykresu funkcji o wektor .
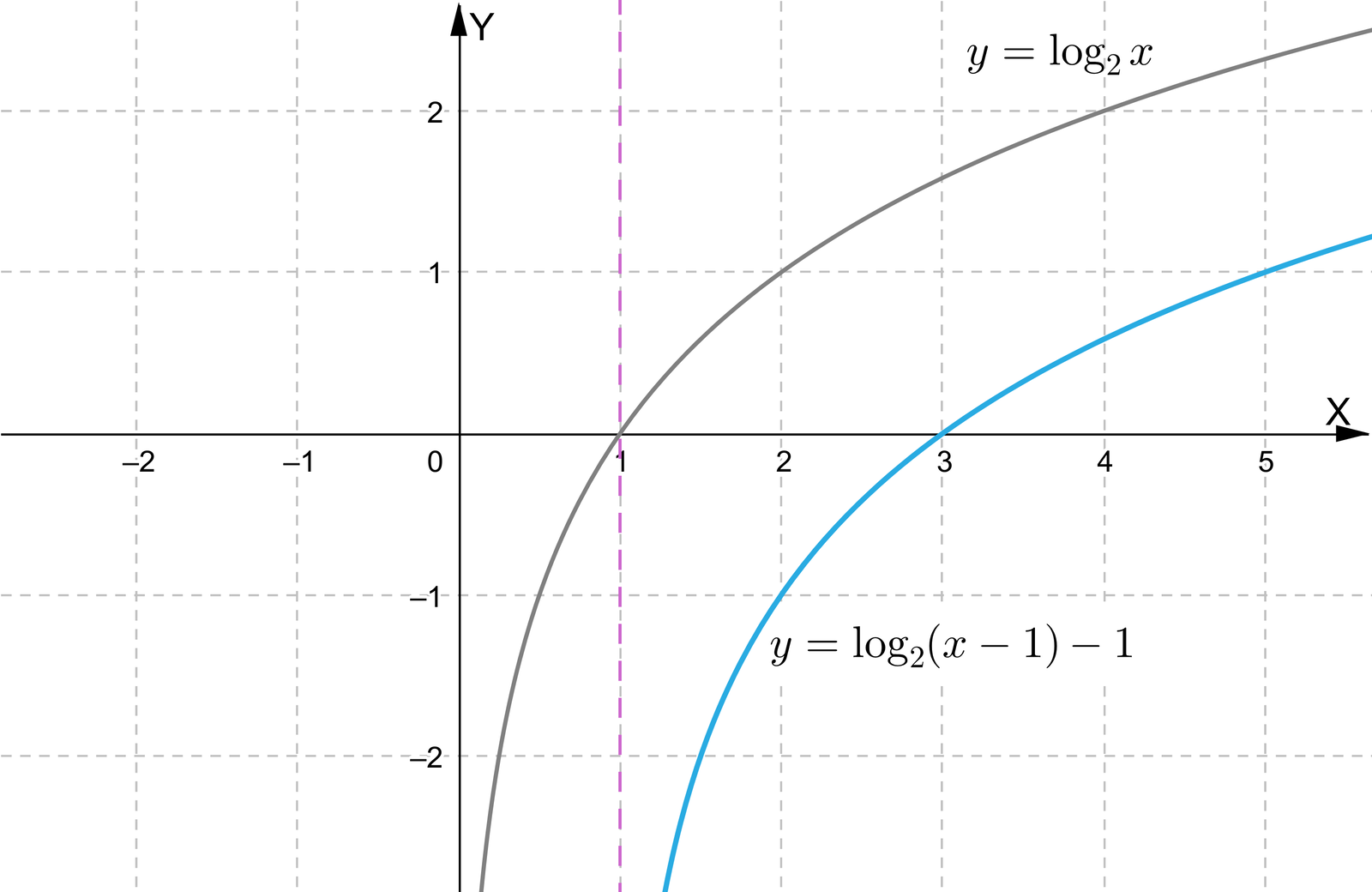
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DroUdnHKF
Polecenie 2
Do wykresu funkcji określonej wzorem należy punkt o współrzędnych .
a) wyznacz wzór tej funkcji,
b) sprawdź, czy punkt o współrzędnych należy do wykresu tej funkcji,
c) podaj miejsce zerowe tej funkcji.