Symulacja interaktywna
Uruchom symulację interaktywną. Ustal położenie wierzchołków trójkąta w taki sposób, aby iloraz długości promieni okręgów opisanego i wpisanego w ten trójkąt był najmniejszy. Sformułuj hipotezę dotyczącą wartości tego ilorazu.
Zapoznaj się z opisem symulacji interaktywnej. Ustal, które położenie wierzchołków trójkąta prowadzi do otrzymania najmniejszego ilorazu długości promieni okręgów opisanego i wpisanego w ten trójkąt. Sformułuj hipotezę dotyczącą wartości tego ilorazu.
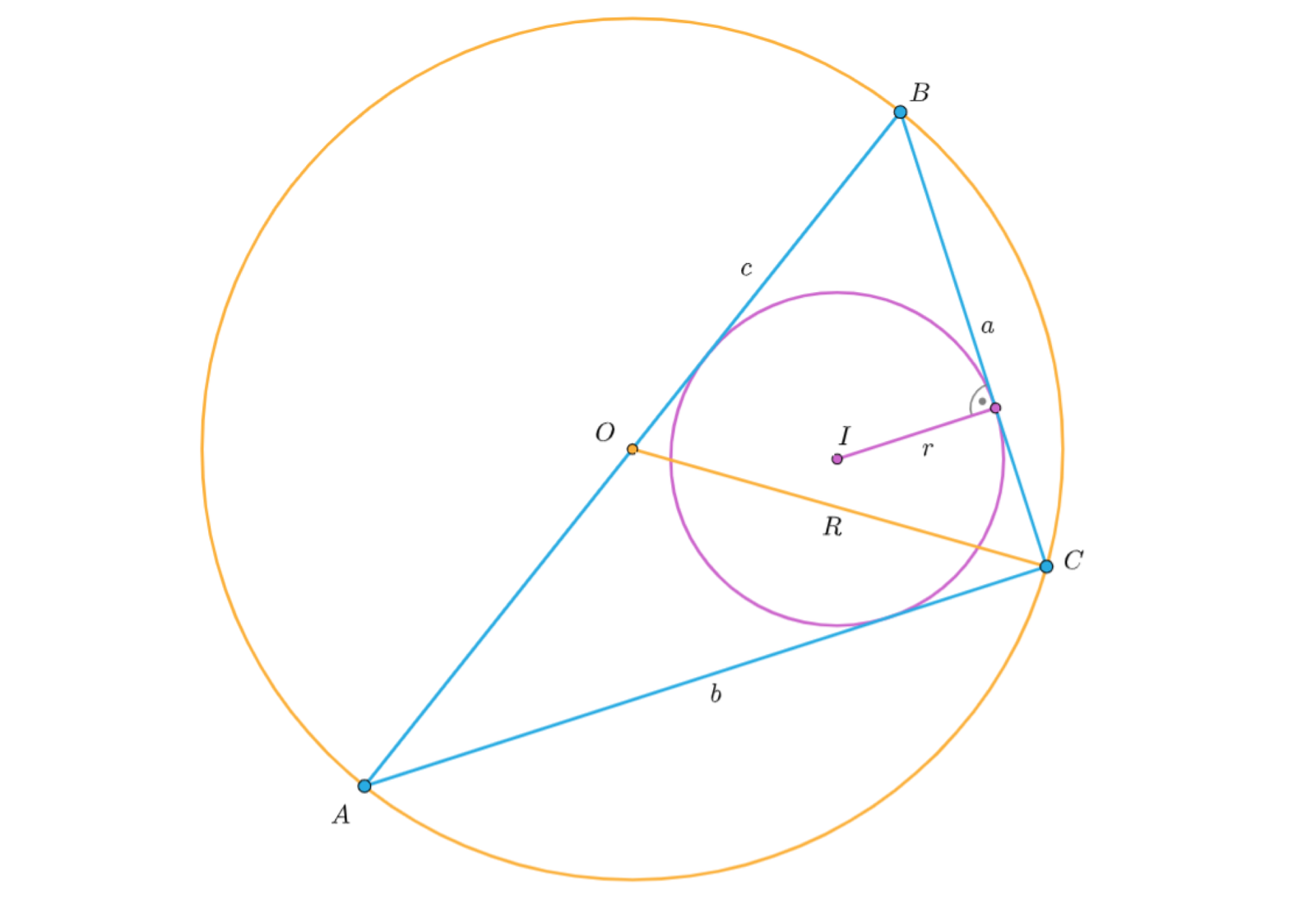
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dt1SIFgcK
Oblicz wartość wyrażenia dla różnych położeń wierzchołków trójkąta. Porównaj otrzymaną wartość z długością promienia okręgu wpisanego w ten trójkąt. Sformułuj odpowiednią hipotezę.
Ustal położenie wierzchołków trójkąta tak, aby iloraz był równy . Oblicz stosunek długości krótszej przyprostokątnej do promienia okręgu wpisanego w trójkąt. Rozwiąż zagadnienie algebraicznie i porównaj otrzymane wyniki.