Aplet
Polecenie 1
Uruchom aplet i przeanalizuj konstrukcję STYCZNEJ DO DANEGO OKRĘGU I RÓWNOLEGŁEJ DO DANEJ PROSTEJ. Zwróć szczególną uwagę na odległości między prostą i otrzymanymi stycznymi.
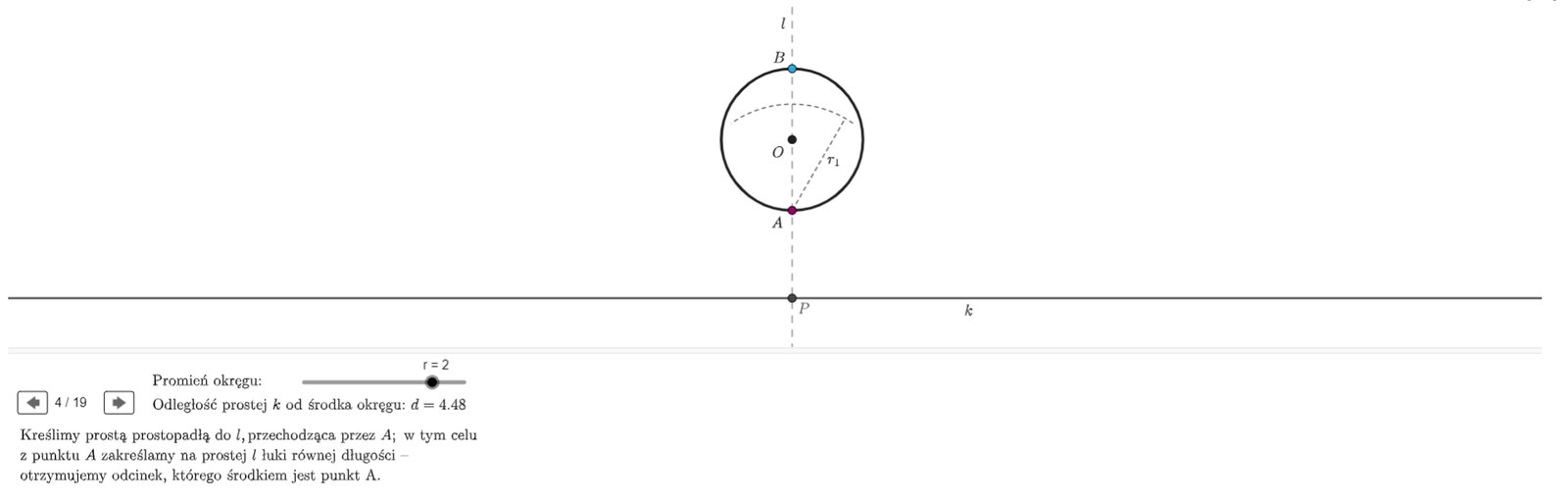
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DzD4d1FH1
- Prosta i okrąg mogą być rozłączne. Wtedy 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza, a odległość od środka okręgu do prostej jest 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza, niż długość promienia okręgu, czyli .
- Prosta i okrąg mogą się przecinać. Wtedy 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza, a odległość od środka okręgu do prostej jest 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza, niż długość promienia okręgu, czyli .
- Prosta i okrąg mogą być styczne. Wtedy 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza, a odległość od środka okręgu do prostej jest 1. większa, 2. mają jeden punkt wspólny, 3. mają dwa punkty wspólne, 4. równa, 5. nie mają punktów wspólnych, 6. mniejsza długości promienia okręgu, czyli .
Polecenie 2
Odległości danej prostej od dwóch stycznych do pewnego okręgu są równe , i są liczbami całkowitymi. Suma jest równa iloczynowi . Oblicz promień okręgu.
Polecenie 3
Poprowadzono styczne do pewnego okręgu, równoległe do prostej . Iloczyn odległości tych stycznych od prostej jest równy , a suma tych odległości jest równa . Oblicz promień okręgu.