Infografika
Polecenie 1
Zapoznaj się z infografiką i rozwiąż polecenie poniżej.
- Funkcja, która nie jest określona na przedziale nie musi przyjmować wszystkich wartości pośrednich.
Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na dodatniej półosi O Y zaznaczono od dołu kolejno wartości alfa, c, beta. Na płaszczyźnie narysowano wykres funkcji składający się z dwóch kawałków krzywej w pofalowanym kształcie. Pierwszy kawałek ma lewy koniec w zamalowanym punkcie na wysokości alfa. Drugi koniec znajduje się w zamalowanym punkcie umiejscowionym na poziomie poniżej wartości c. Na poziomie c linią przerywaną narysowano poziomą prostą. Powyżej wartości c znajduje się druga składowa wykresu o lewym końcu w zamalowanym punkcie powyżej wartości c i o prawym końcu w zamalowanym punkcie na poziomie beta. - Funkcja nieciągła mimo, że jest określona na przedziale, nie musi przyjmować wszystkich wartości pośrednich.
Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na dodatniej półosi O Y zaznaczono od dołu kolejno wartości alfa, c, beta. Na płaszczyźnie narysowano wykres funkcji składający się z dwóch kawałków krzywej w pofalowanym kształcie. Pierwszy kawałek ma lewy koniec w zamalowanym punkcie na wysokości beta. Z prawej strony kawałek ograniczony jest niezamalowanym punktem znajdującym się powyżej wartości c. Na poziomie c linią przerywaną narysowano poziomą prostą. Poniżej wartości c znajduje się druga składowa wykresu o lewym końcu w zamalowanym punkcie poniżej wartości c i o prawym końcu w zamalowanym punkcie na poziomie alfa.
Polecenie 2
Wskaż wykresy tych funkcji, które spełniają założenia twierdzenia Darboux.
- Opis poprawnej ilustracji 1
- Opis poprawnej ilustracji 2
- Opis ilustracji 3
- Opis ilustracji 4
- Opis ilustracji 5
- Opis poprawnej ilustracji 6

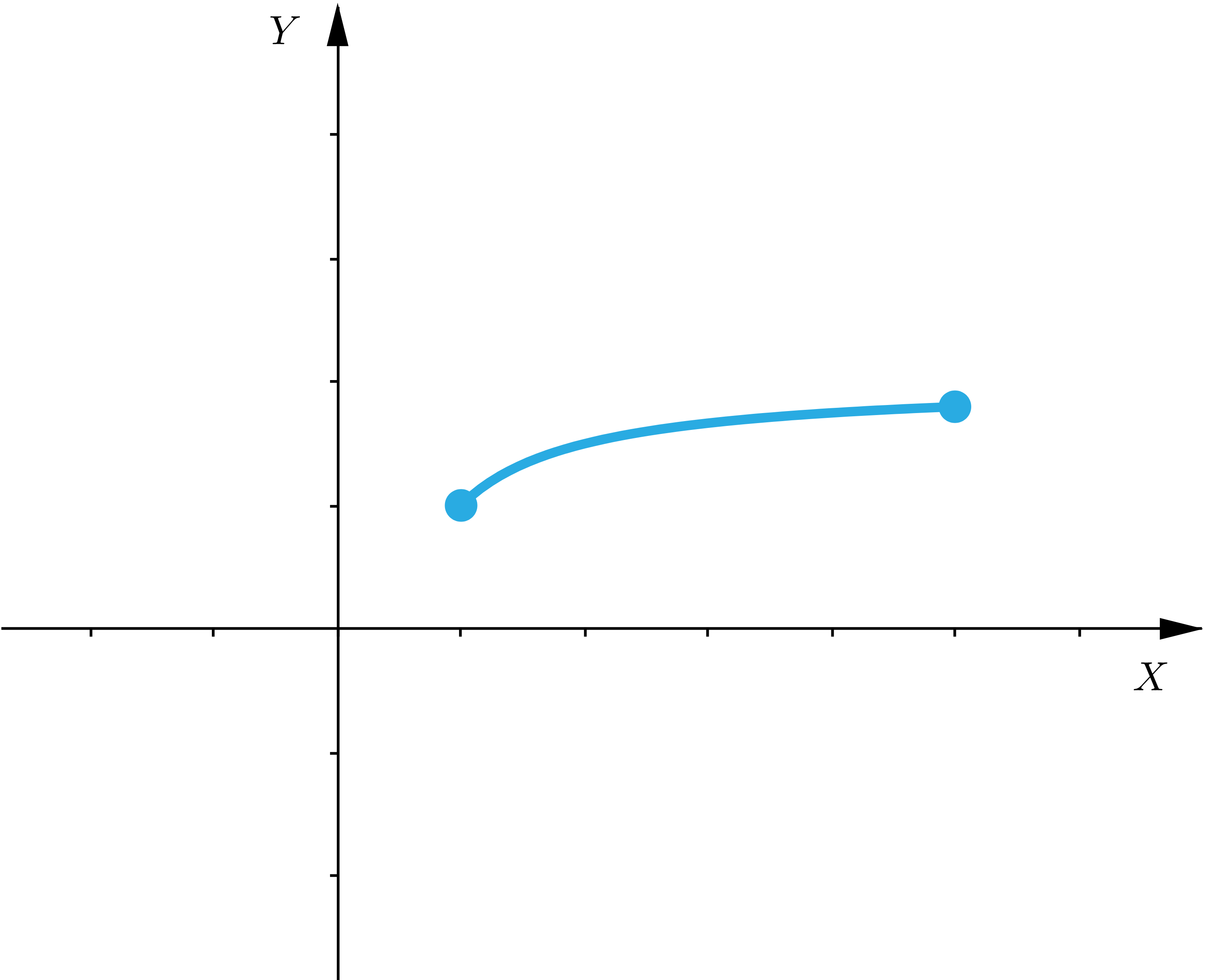
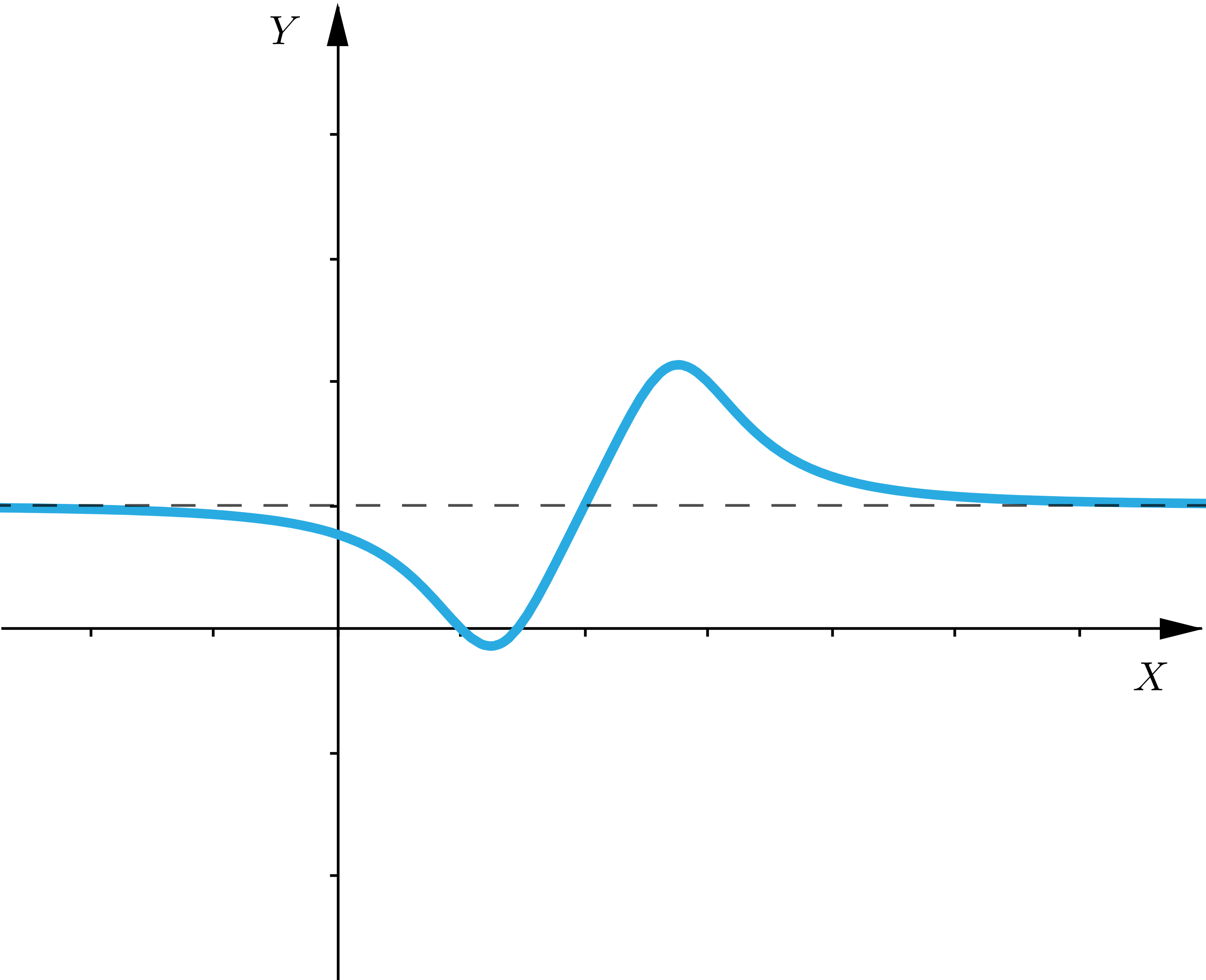
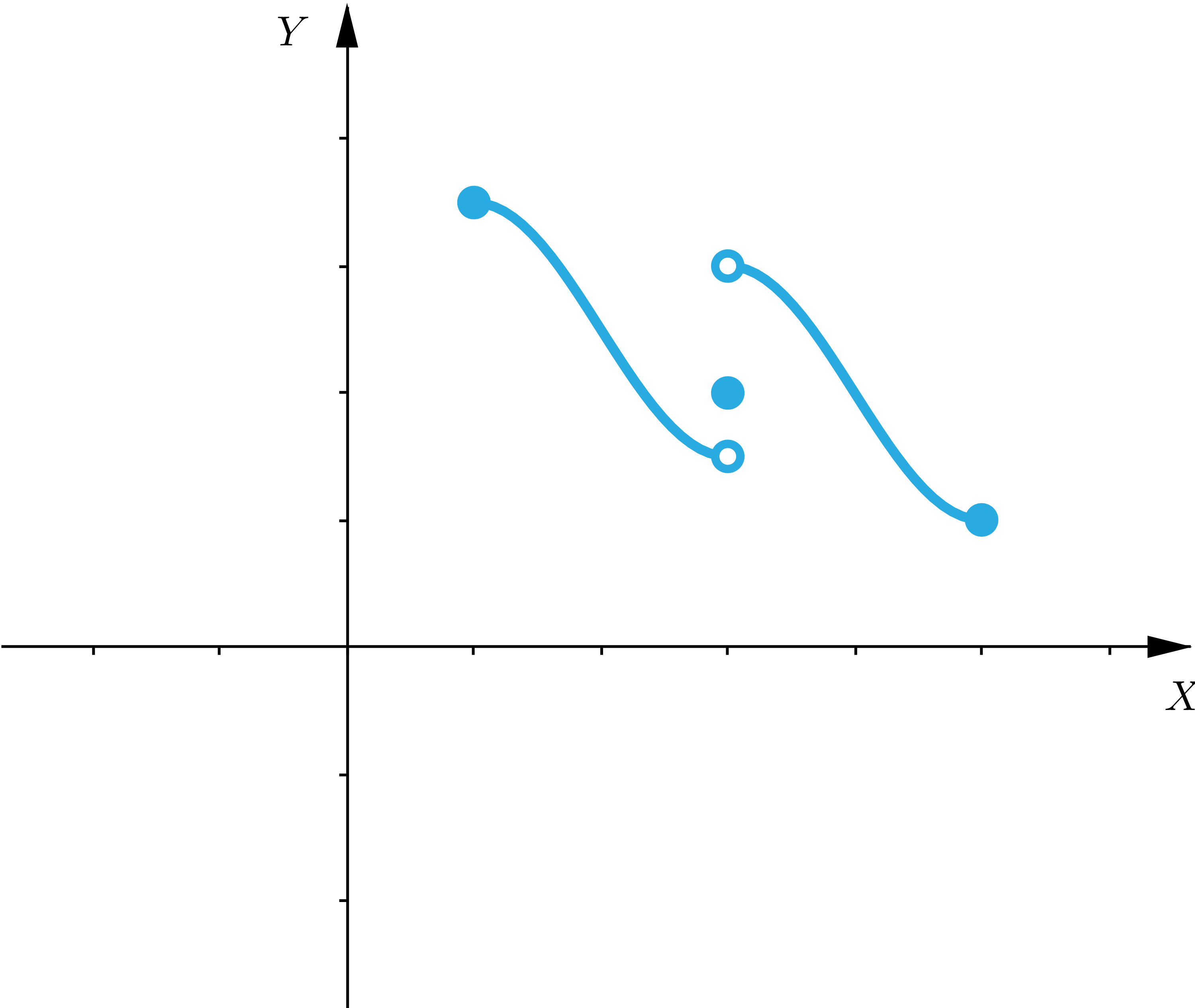

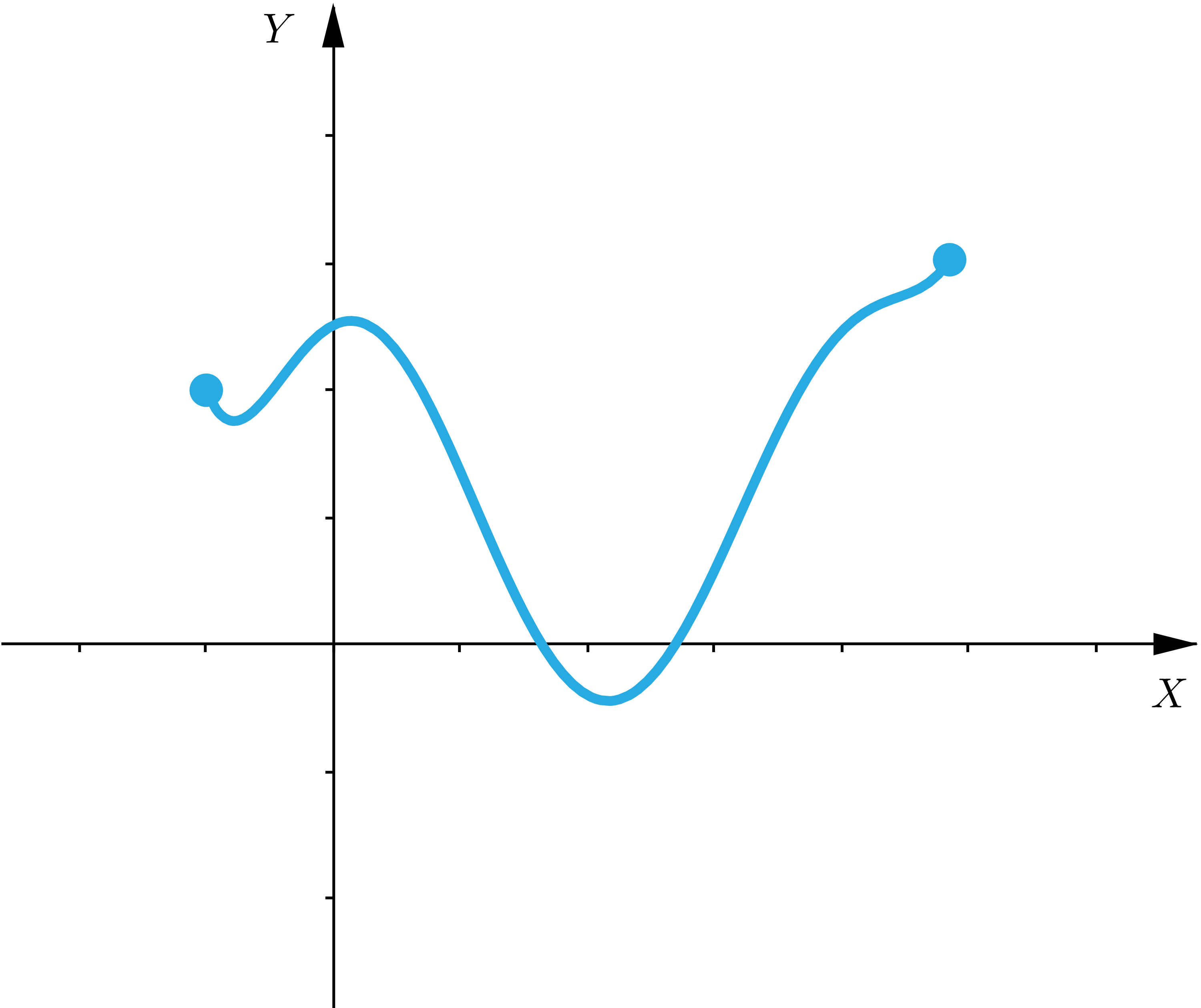
Funkcje niespełniające twierdzenia Darboux to na przykład:
- Funkcja, która nie jest określona na przedziale 1. maksimum, 2. ekstremum, 3. minimum, 4. nie musi przyjmować wszystkich wartości pośrednich, 5. nieciągła, 6. musi przyjmować wszystkie wartości pośrednie, 7. ciągła.
- Funkcja 1. maksimum, 2. ekstremum, 3. minimum, 4. nie musi przyjmować wszystkich wartości pośrednich, 5. nieciągła, 6. musi przyjmować wszystkie wartości pośrednie, 7. ciągła mimo, że jest określona na przedziale, nie musi przyjmować wszystkich wartości pośrednich.