Niech funkcja $f:⟨a,b⟩⟶\mathrm{ℝ}$ będzie funkcją ciągłąfunkcja ciągłafunkcją ciągłą, oznaczmy:

Wówczas dla każdego $c\in ⟨\alpha ,\beta ⟩$ istnieje taki $x\in ⟨a,b⟩$, że $f\left(x\right)=c$.

R10vFiXqRww7Q

Ilustracja przedstawia pierwszą ćwiartkę układu współrzędnych. Na płaszczyźnie narysowano wykres funkcji funkcji będący kawałkiem falistej krzywej. Punkt początkowy będący jednocześnie maksimum funkcji zrzutowano na obie osie. Na osi X mamy z rzutu punkt a, na osi Y mamy wartość beta. Prawy koniec wykresu również zrzutowano na obie osie. Na osi X z rzutu zaznaczono wartość b, na osi Y zaznaczono wartość alfa poniżej beta. Na wykresie zaznaczono punkt, który również zrzutowano: na osi X oznaczono wartość x, a na osi Y wartość c, która znajduje się między wartościami alfa i beta.

Niech funkcja $f:X\to Y$. Obrazem zbioru $A\subset X$ przez funkcję $f$ nazywamy zbiór

Niech funkcja $f:A⟶\mathrm{ℝ}$ będzie funkcją ciągłąfunkcja ciągłafunkcją ciągłą. Wówczas $f(⟨a,b⟩)$ jest przedziałem dla każdego $⟨a,b⟩\subset A$.

Rozważmy funkcję $f:\mathrm{ℝ}⟶\mathrm{ℝ}$ daną wzorem $f\left(x\right)=x-\cos \left(\sin \right(x^2\left)\right)$.

Nietrudno zauważyć, że $x\in \mathrm{ℝ}$ jest rozwiązaniem równania dokładnie wtedy, gdy $f\left(x\right)=0$. Ponadto funkcja $f$ jest ciągła. Policzmy teraz

$f(-2)=-2-\cos (\sin 4)\le -2+1=-1$
oraz
$f(2)=2-\cos (\sin 4)\ge 2-1=1$.

Na mocy twierdzenia Darboux otrzymujemy, że funkcja $f$ przyjmuje wszystkie wartości z przedziału $⟨-1,1⟩$. Tym samym istnieje taki $x\in ⟨-2,2⟩$, że $f\left(x\right)=0$.

Rozważmy funkcję $f:⟨-\pi ,-2⟩\cup ⟨2,\pi ⟩⟶\mathrm{ℝ}$ daną wzorem $f\left(x\right)=x-\sin \left(x\right)$.

Wówczas wykres funkcji $f$ wygląda następująco.

R1bfT2xhFXbxI

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pi do pi oraz z pionową osią Y od minus pi do pi. Na płaszczyźnie narysowano wykres funkcji składający się z dwóch ukośnych kawałków krzywej. Pierwszy ma końce w zamalowanych punktach $\left(-\pi ;-\pi \right)$ oraz $\left(-2;-1,09\right)$. Drugi kawałek krzywej ma współrzędne $\left(2;1,09\right)$ oraz $\left(\pi ;\pi \right)$

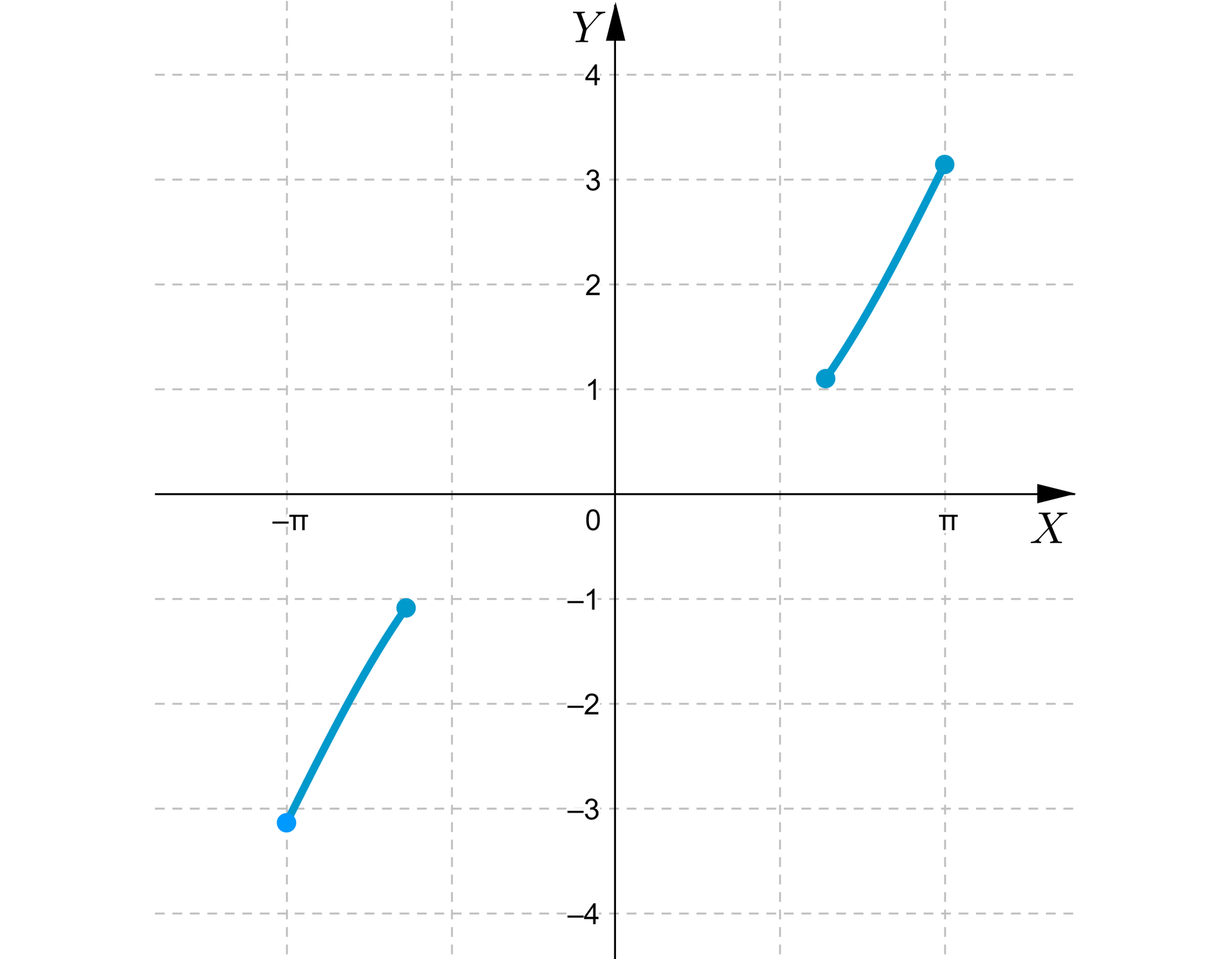
Tym samym, mimo tego, że $f\left(-\pi \right)=-\pi$ oraz $f\left(\pi \right)=\pi$, to nie istnieje $x\in ⟨-\pi ,-2⟩\cup ⟨2,\pi ⟩$ spełniający $f\left(x\right)=0$, ponieważ $0\in ⟨-\pi ,\pi ⟩$.

Niech funkcja $f:⟨-1,1⟩⟶\mathrm{ℝ}$ będzie określona wzorem

Wtedy wykres $f$ ma postać.

R1QtRmu4RDCR4

Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus dwóch do dwóch. Na płaszczyźnie narysowano wykres funkcji składający się z dwóch kawałków krzywej. Pierwszy ma lewy koniec w zamalowanym punkcie $\left(-1;-2\right)$ i biegnie łukiem w prawo. Z prawej strony jest on ograniczony niezamalowanym punktem $\left(0;-1\right)$. Drugi kawałek krzywej ma końce w zamalowanych punktach o współrzędnych $\left(0;0\right)$ oraz $\left(1;0,84\right)$.

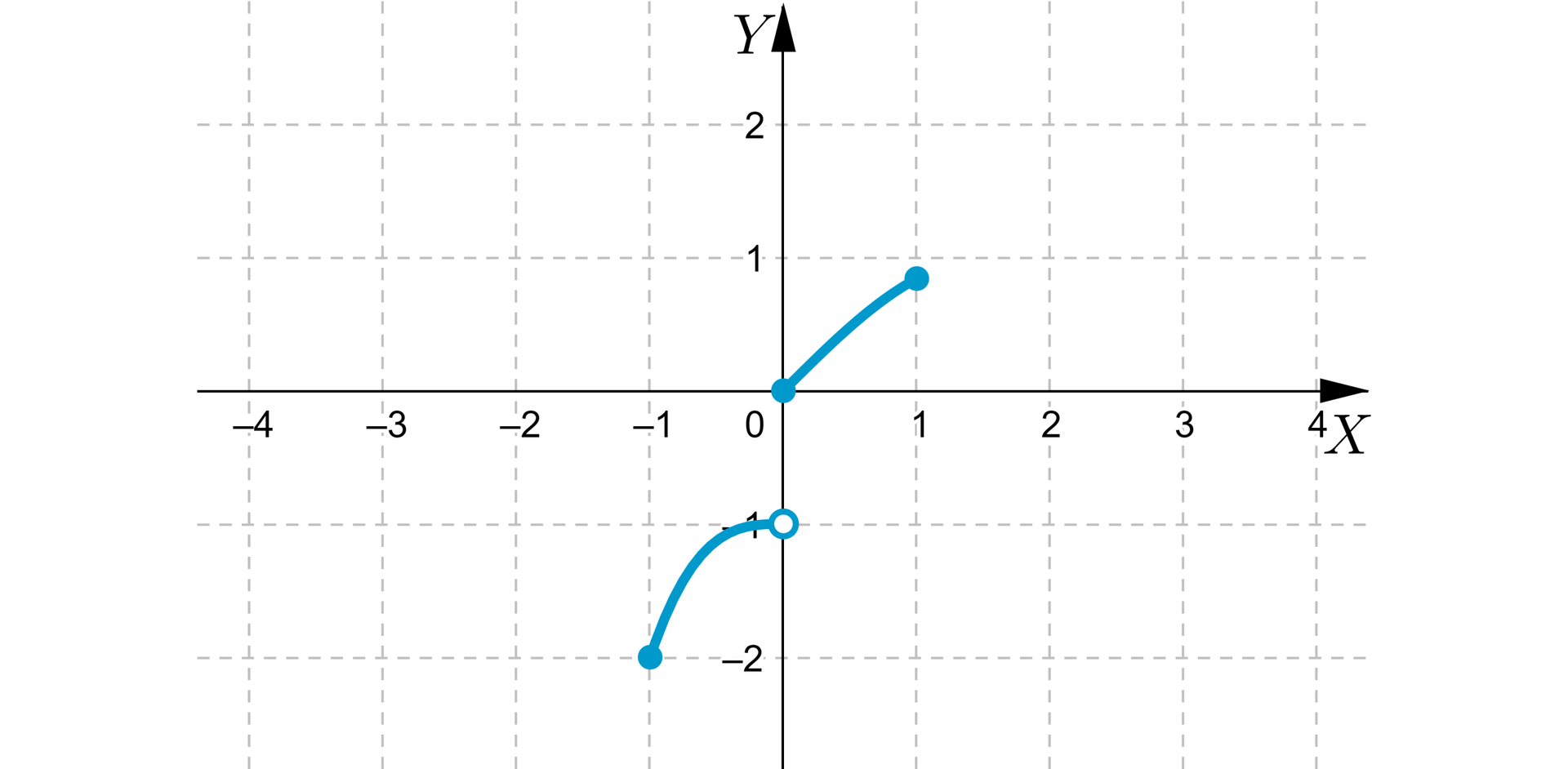
Zatem mimo tego, że $f\left(-1\right)=-2$, $f\left(0\right)=0$ oraz $-\frac{1}{2}\in ⟨-2,0⟩$, to wartość $\left(-\frac{1}{2}\right)$ nie jest przyjmowana

Udowodnimy, że dla funkcji ciągłej $f:⟨-1,1⟩\to \mathrm{ℝ}$, $f\left(x\right)=x^2+3x$ spełniona jest teza Twierdzenia Darboux (1).

Skoro $f\left(-1\right)=-2$ i $f\left(1\right)=4$, to $\alpha =-2$ i $\beta =4$. Weźmy $c\in ⟨-2,4⟩$. Pokażemy, że istnieje takie $x_2\in ⟨-1,1⟩$, że $f\left(x_2\right)=c$.

W tym celu rozwiążemy równanie $x^2+3x=c$, tj. $x^2+3x-c=0$. Wyróżnik tego trójmianu to $\Delta =9+4c$. Zauważmy, że dla $c\in ⟨-2,4⟩$ spełniona jest nierówność $\Delta >0$. Mamy zatem dwa pierwiastki $x_1=\frac{-3-\sqrt{9+4c}}{2}$ oraz $x_2=\frac{-3+\sqrt{9+4c}}{2}$. Pokażemy, że $x_2$ jest szukanym argumentem, czyli że $x_2\in ⟨-1,1⟩$.

Mamy ciąg równoważnych nierówności: $\frac{-3+\sqrt{9+4c}}{2}\le 1$

$-3+\sqrt{9+4c}\le 2$

$\sqrt{9+4c}\le 5$

Obie strony nierówności są liczbami większymi od $0$ , więc możemy podnieść nierówność stronami do kwadratu. Tym samym otrzymujemy nierówność $9+4c\le 25$, która jest prawdziwa dla $c\le 4$.

Pozostaje pokazać, że dla rozważanych wartości $c$ spełniona jest nierówność $x_2\ge -1$, czyli

$\frac{-3+\sqrt{9+4c}}{2}\ge -1$

$-3+\sqrt{9+4c}\ge -2$

$\sqrt{9+4c}\ge 1$, co również jest spełnione gdy $c\ge -2$.

Zatem $x_2\in ⟨-1,1⟩$ oraz $f\left(x_2\right)=c$, więc spełnione jest teza Twierdzenia Darboux (1).

dla wielomianu $a{x}^2+bx+c$ liczba dana wzorem $b^2-4ac$

funkcja spełniająca jeden z równoważnych warunków ciągłości (Cauchy’ego lub Heinego)