Jednomiany i sumy algebraiczne
Wyrażenie algebraiczne to takie wyrażenie, w którym występują liczby i litery połączone znakami działań matematycznych oraz nawiasami.

Film dostępny na portalu epodreczniki.pl
Animacja
Wyrażenia algebraiczne utworzone są z liczb, liter, znaków działań matematycznych oraz nawiasów.
W wyrażeniach algebraicznych można pominąć znak mnożenia między dwiema literami oraz liczbą i literą, jeżeli liczba występuje w tym zapisie jako pierwsza.
Za pomocą wyrażeń algebraicznych możemy zapisywać na przykład wzory matematyczne. Nazwę wyrażenia algebraicznego określa działanie, które zgodnie z kolejnością wykonywania działań byłoby wykonywane jako ostatnie.
Zapiszemy za pomocą wyrażeń algebraicznych zwroty matematyczne:

Film dostępny na portalu epodreczniki.pl
Animacja
Spośród poniższych wyrażeń algebraicznych wybierzmy liczby, litery lub iloczyn liczb i liter.

Film dostępny na portalu epodreczniki.pl
Animacja
Jednomianem nazywamy wyrażenie algebraiczne, które jest liczbą, literą lub iloczynem liczb i liter.
Wyrażenie algebraiczne zbudowane jest z jednomianów.
Wyrażenie algebraiczne | Jednomiany tworzące to wyrażenie |
, , | |
, , | |
, , |
Występujący w jednomianie znak mnożenia często pomijamy, na przykład:
Jeżeli w jednomianie pierwszym czynnikiem jest litera, a drugim liczba, to znaku mnożenia nie pomijamy. Na przykład:
Uporządkujemy jednomian .
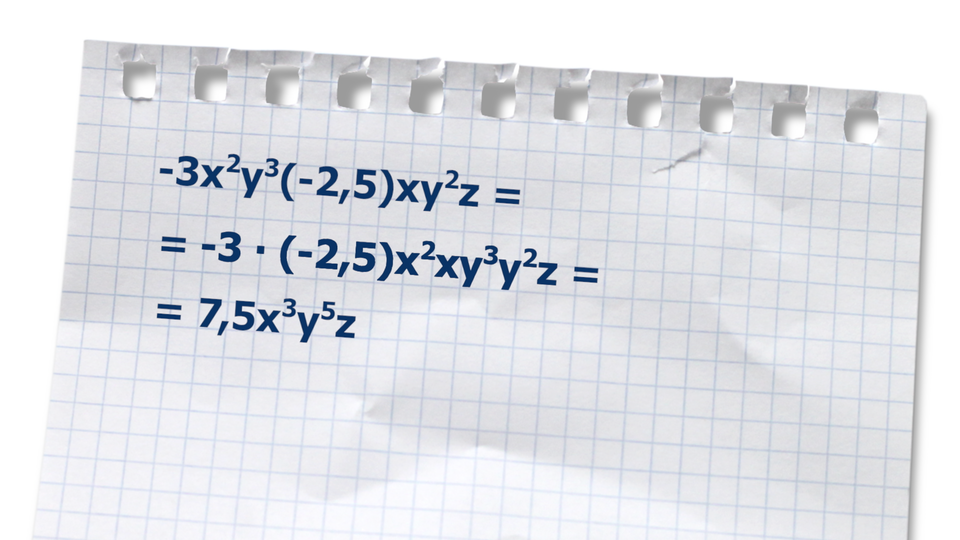
Film dostępny na portalu epodreczniki.pl
Animacja

Film dostępny na portalu epodreczniki.pl
Animacja

Film dostępny na portalu epodreczniki.pl
Animacja
Jednomianem jest wyrażenie:
Połącz w pary jednomiany przed uporządkowaniem z odpowiadającymi im jednomianami po uporządkowaniu.
<span aria-label="dwa początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, dwa, y indeks górny, dwa, z indeks górny, trzy" role="math"><math><mn>2</mn><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>3</mn></msup></math></span>, <span aria-label="trzy x indeks górny, trzy, y indeks górny, dwa, z indeks górny, dwa" role="math"><math><mn>3</mn><msup><mi>x</mi><mn>3</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>2</mn></msup></math></span>, <span aria-label="początek ułamka, jeden, mianownik, dwa, koniec ułamka, a indeks górny, trzy, b indeks górny, cztery" role="math"><math><mfrac><mn>1</mn><mn>2</mn></mfrac><msup><mi>a</mi><mn>3</mn></msup><msup><mi>b</mi><mn>4</mn></msup></math></span>, <span aria-label=" minus, cztery a b indeks górny, trzy" role="math"><math><mo>-</mo><mn>4</mn><mi>a</mi><msup><mi>b</mi><mn>3</mn></msup></math></span>, <span aria-label="początek ułamka, dwanaście, mianownik, dwadzieścia pięć, koniec ułamka, a indeks górny, trzy, b indeks górny, cztery" role="math"><math><mfrac><mn>12</mn><mn>25</mn></mfrac><msup><mi>a</mi><mn>3</mn></msup><msup><mi>b</mi><mn>4</mn></msup></math></span>, <span aria-label="trzy początek ułamka, jeden, mianownik, pięć, koniec ułamka, x indeks górny, trzy, y indeks górny, dwa, z indeks górny, trzy" role="math"><math><mn>3</mn><mfrac><mn>1</mn><mn>5</mn></mfrac><msup><mi>x</mi><mn>3</mn></msup><msup><mi>y</mi><mn>2</mn></msup><msup><mi>z</mi><mn>3</mn></msup></math></span>, <span aria-label=" minus, osiem a b indeks górny, trzy" role="math"><math><mo>-</mo><mn>8</mn><mi>a</mi><msup><mi>b</mi><mn>3</mn></msup></math></span>
Jednomian powstanie po uporządkowaniu jednomianu
Uporządkuj jednomiany.
Przeciągnij i upuść odpowiednie jednomiany tak, aby prawdziwe były podane równości.
, , , , , , ,
a) ............
b) ............
c) ............
d) ............
e) ............
Po redukcji wyrazów podobnych sumy algebraicznej otrzymamy
Zredukuj wyrazy podobne sumy algebraicznej.
Po opuszczeniu nawiasów i redukcji wyrazów podobnych wyrażenie będzie miało postać
Po opuszczeniu nawiasów i redukcji wyrazów podobnych wyrażenie ma postać
Zapisz podane wyrażenia bez użycia nawiasów i zredukuj wyrazy podobne.
W trójkącie długość podstawy wynosi , wysokość opuszczona na podstawę z wierzchołka stanowi długości podstawy. Zapisz w postaci uporządkowanego jednomianu wyrażenie opisujące pole tego trójkąta.
Pole trójkąta jest opisane za pomocą wyrażenia , a jego podstawa za pomocą wyrażenia . Zapisz w postaci uporządkowanego jednomianu wyrażenie opisujące wysokość trójkąta opuszczoną na tę podstawę.
Jeden z boków prostokąta ma długość , a drugi stanowi tej długości. Zapisz w postaci uporządkowanych jednomianów wyrażenia opisujące obwód i pole tego prostokąta.
Tort przygotowany na przyjęcie urodzinowe Ali ważył kilogramów. Ala odkroiła tortu dla brata i siostry, którzy nie mogli być obecni na przyjęciu. Pozostałą część podzieliła równo pomiędzy wszystkich uczestników przyjęcia. Ile ważył kawałek tortu, jaki otrzymał każdy uczestnik, jeżeli Ala zaprosiła koleżanek i kolegów?
Zosia zrobiła łańcuch choinkowy o długości Łańcuch zrobiony przez Olę stanowił długości łańcucha Zosi. Łańcuch Kasi był razy dłuższy od łańcucha Oli, a łańcuch Asi był razy dłuższy od łańcucha Kasi. Jaka była długość łańcucha wykonanego przez Asię?
Rozstrzygnij, czy równość jest prawdziwa, czy fałszywa.
Utworzono liczbę trzycyfrową o cyfrze setek cyfrze dziesiątek i cyfrze jedności Od tej liczby odjęto liczbę trzycyfrową o cyfrze setek cyfrze dziesiątek i cyfrze jedności Zapisz za pomocą wyrażenia algebraicznego liczbę będącą wynikiem tego odejmowania.