Pojęcie ciągu. Ciąg jako funkcja zmiennej naturalnej

Film dostępny na portalu epodreczniki.pl
Animacja
Klasa pojechała na białą szkołę. Tomek, Małgosia, Julka, Franek i Jurek stoją w kolejce do wyciągu narciarskiego. Każde z nich zajmuje konkretną pozycję w kolejce. Możemy powiedzieć, że każdej z pozycji, czyli kolejnej liczbie naturalnej od do , przyporządkowana jest konkretna osoba. Takie przyporządkowanie nazywamy ciągiem.
Liczbie (pierwszemu miejscu w kolejce) przyporządkowany jest Tomek.
Liczbie (drugiemu miejscu w kolejce) przyporządkowana jest Małgosia.
Liczbie (trzeciemu miejscu w kolejce) przyporządkowana jest Julka.
Liczbie (czwartemu miejscu w kolejce) przyporządkowany jest Franek.
Liczbie (piątemu miejscu w kolejce) przyporządkowany jest Jurek.

Film dostępny na portalu epodreczniki.pl
Animacja
Ciągiem nazywamy funkcję, określoną w zbiorze liczb całkowitych dodatnich. Wartości tej funkcji dla kolejnych liczb naturalnych nazywamy wyrazami ciągu.
Jeżeli ciąg jest nieskończony, to jego dziedziną jest zbiór dodatnich liczb całkowitych. Dziedziną ciągu skończonego jest zbiór , gdzie jest ustaloną dodatnią liczbą całkowitą.
Ciąg dwuwyrazowy jest parą uporządkowaną, z którą spotkaliśmy się, np. podając współrzędne punktu w prostokątnym układzie współrzędnych na płaszczyźnie. Zwróćmy uwagę, że pary uporządkowane i są różne.
Ciąg opisany w przykładzie powyżej jest skończony, ponieważ w kolejce stoi osób, czyli skończona liczba osób. Dziedziną tego ciągu jest zbiór .
Jeżeli elementy jakiegoś zbioru ponumerujemy, a więc ustalimy kolejność tych elementów, to w ten sposób otrzymamy ciąg.
W praktyce będziemy zajmować się najczęściej ciągami liczbowymi, czyli takimi, których wyrazy są liczbami. Ciąg oznaczamy zazwyczaj itd. Natomiast oznacza -ty wyraz ciągu , na przykład drugi wyraz ciągu to .
Jeżeli ciąg z podanego wyżej przykładu oznaczymy , to Tomek, Małgosia, Julka, Franek, Jurek.
Rozpatrzmy ciąg składający się z wyrazów, które są kolejnymi początkowymi liczbami pierwszymi. Przypomnijmy, że najmniejszą liczbą pierwszą jest . Zatem
Ciąg liczbowy, podobnie jak inne funkcje, można opisać na różne sposoby, np. narysować jego wykres. Oto wykres tego ciągu:

Oblicz sześć początkowych wyrazów ciągu określonego wzorem . Aby obliczyć wyraz o numerze , należy podnieść numer wyrazu do kwadratu i dodać do niego potrojony numer tego wyrazu.
W ten sposób obliczamy
Tak samo możemy obliczyć wyraz o dowolnie wybranym numerze, np.
Podany przez nas wzór ma tę własność, że każdy wyraz ciągu jest uzależniony od numeru tego wyrazu, tego typu wzór określający ciąg nazywamy wzorem ogólnym.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DpLrb1VJR
Dany jest ciąg ułamków takich, że licznik każdego z tych ułamków, a więc każdego wyrazu tego ciągu równy jest numerowi, a mianownik jest o większy od licznika. Zatem ciąg ten ma postać . Jego -ty wyraz możemy opisać wzorem ogólnym . Znając wzór, możemy obliczyć dowolny wyraz tego ciągu, np.
Dany jest ciąg nieskończony o wzorze ogólnym . Wypiszmy wszystkie wyrazy ujemne tego ciągu.
Zauważmy, że każdy wyraz ciągu to ułamek , którego licznik, czyli , jest dodatni, gdyż . Zatem ułamek jest ujemny, gdy jego mianownik jest ujemny, czyli gdy , a więc . Wynika stąd, że ujemnymi wyrazami są tylko trzy początkowe wyrazy:
Ciąg określony jest wzorem ogólnym .
Oblicz wyrazy , , , .
Korzystając z wzoru ogólnego, mamy:
Wykaż, że oraz.
Obliczmy
co oznacza, że oraz .
Ciąg określony jest wzorem ogólnym .
Uzasadnij, że żaden wyraz ciągu nie jest równy zero.
Przypuśćmy, że któryś z wyrazów jest równy zero, a więc . Zatem , czyli lub . Stąd lub . Żadna z tych równości nie jest prawdziwa, gdyż to numer wyrazu ciągu i jest dodatnią liczbą całkowitą. To oznacza, że żaden wyraz tego ciągu nie jest równy .Który wyraz tego ciągu jest równy ?
Podobnie jak poprzednio, rozwiązujemy równanie , czyli . Po przekształceniu tego równania otrzymujemy równanie kwadratowe , które ma dwa rozwiązania lub . Tylko drugie z tych rozwiązań jest to dodatnia liczba całkowita, więc . Oznacza to, że tylko trzeci wyraz tego ciągu jest równy .
Ciąg określony jest wzorem ogólnym . Który wyraz tego ciągu jest równy ?
Rozwiązujemy równanie , czyli . Stąd wynika, że , więc . Zatem jedynie .
Ciąg określony jest wzorem ogólnym . Oblicz , , .
Obliczamy
Zauważmy, że podanie kilku początkowych wyrazów ciągu nie pozwala jednoznacznie obliczyć kolejnych jego wyrazów ani określić wzoru ogólnego tego ciągu. Rozpatrzmy nieskończony ciąg . Można byłoby przypuszczać, że jest to ciąg z poprzedniego przykładu, a więc ciąg określony wzorem ogólnym . Można byłoby też przyjąć, że wzór ogólny tego ciągu to lub . Wówczas jednak inne byłyby już czwarte wyrazy tych ciągów. W pierwszym , w drugim , a w ostatnim .
Jeżeli oprócz podania początkowych wyrazów ciągu określimy również zasadę opisującą tworzenie kolejnych jego wyrazów z poprzednich wyrazów, to wtedy ciąg określimy w sposób jednoznaczny. Na przykład gdybyśmy przy określaniu ciągu nieskończonego podali jeszcze, że każdy jego wyraz, począwszy od wyrazu drugiego, jest o większy od wyrazu bezpośrednio go poprzedzającego, to wówczas obie te informacje moglibyśmy zapisać krótko w postaci , dla . W ten sposób można obliczyć kolejne wyrazy ciągu:
Jednak aby obliczyć np. , musimy najpierw obliczyć itd. Zauważmy jednak, że ten sam ciąg opisuje wzór ogólny , który pozwala obliczyć dowolny wyraz ciągu, np.
Wyznacz wzór ogólny ciągu, którego pierwszy wyraz jest równy , a każdy następny wyraz jest o większy od poprzedniego.
Informacje podane w poleceniu możemy zapisać w postaci , dla .
Pierwszy wyraz ciągu to . Obliczmy kilka następnych wyrazów tego ciągu:
Zauważmy, że trzeci wyraz jest większy od pierwszego wyrazu o dwie trójki, czyli o , czwarty jest większy od pierwszego o trzy trójki, czyli o . Zatem wyraz o numerze jest większy od wyrazu pierwszego o trójek. Wzór ogólny tego ciągu możemy więc zapisać w postaci
Zbadamy teraz, rozpatrując kilka przykładów, jak zachowują się kolejne wyrazy ciągu. Interesować nas będzie, czy wyrazy ciągu rosną, maleją, czy nie zmieniają się.
Rozpatrzmy nieskończone ciągi , , określone wzorami ogólnymi , , . Obliczymy trzy pierwsze wyrazy każdego z tych ciągów:
Zauważmy, że
Obliczone wyrazy ciągu są coraz większe, a więc rosną. Tak też się dzieje z kolejnymi wyrazami tego ciągu, gdyż przy coraz większym rośnie też wartość wyrażenia . Mówimy wówczas, że ciąg jest rosnący.
To samo możemy też stwierdzić, gdy zauważymy, że wykres ciągu składa się z punktów leżących na prostej o równaniu . Ta prosta jest wykresem rosnącej funkcji liniowej. Zatem i ciąg jest rosnący.

Obliczone wyrazy ciągu są coraz mniejsze, następne również maleją. Jest tak dlatego, że przy zwiększaniu maleje ułamek , a to oznacza, że maleje też różnica . Ciąg jest więc malejący.
Podobnie jak poprzednio do tego samego wniosku możemy dojść, zauważając, że wykres ciągu składa się z punktów leżących na hiperboli o równaniu . Ta hiperbola jest wykresem funkcji, która w przedziale jest malejąca. Zatem i ciąg jest malejący.

Obliczone wyrazy ciągu maleją, czwarty wyraz jest mniejszy od trzeciego , ale już kolejne wyrazy nie są coraz mniejsze. Piąty wyraz jest większy od czwartego (. Ciąg ten nie jest więc malejący, nie jest też rosnący. To samo możemy zauważyć, patrząc na wykres , który składa się z punktów leżących na paraboli o równaniu . Parabola ta jest wykresem funkcji malejącej w przedziale , a rosnącej w przedziale . Funkcja ta nie jest więc monotoniczna w przedziale , a w tym przedziale leżą wszystkie numery wyrazów ciągu.
R145z2gdXfwE11 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Film dostępny na portalu epodreczniki.pl
Animacja prezentuje punkty w układzie współrzędnych, które ilustrują ciąg rosnący. Dla argumentów n oraz n +1 (n

Film dostępny na portalu epodreczniki.pl
Animacja prezentuje punkty w układzie współrzędnych, które ilustrują ciąg malejący. Dla argumentów n oraz n +1 (n (a z indeksem dolnym n +1).

Film dostępny na portalu epodreczniki.pl
Animacja prezentuje punkty w układzie współrzędnych, które ilustrują ciąg nierosnący. Dla argumentów n oraz n +1 (n

Film dostępny na portalu epodreczniki.pl
Animacja prezentuje punkty w układzie współrzędnych, które ilustrują ciąg niemalejący. Dla argumentów n oraz n +1 (n
Film dostępny na portalu epodreczniki.pl
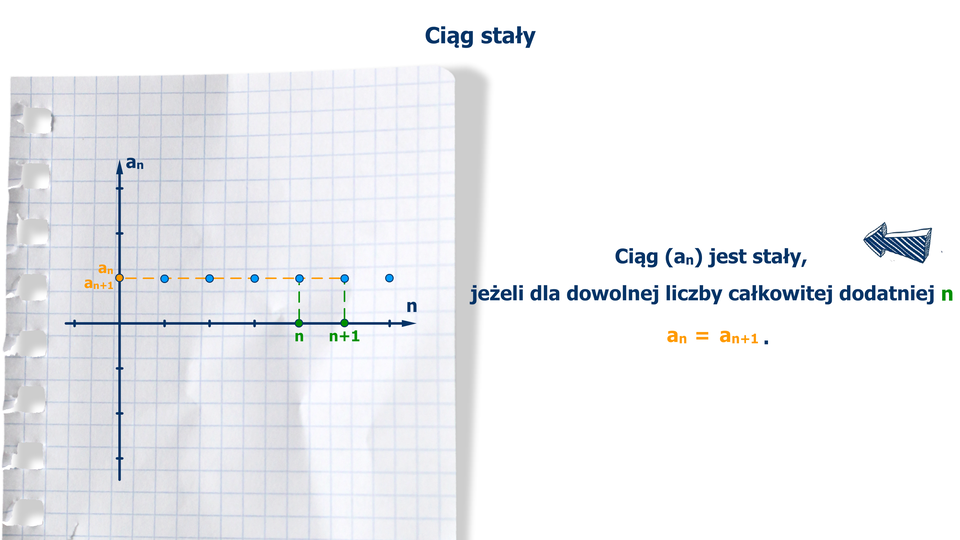
Animacja prezentuje punkty w układzie współrzędnych, które ilustrują ciąg stały. Dla argumentów n oraz n +1 (n

Film dostępny na portalu epodreczniki.pl
Animacja w dwóch układach współrzędnych prezentuje punkty, które ilustrują ciągi naprzemienne o wzorach: (a z indeksem dolnym n) =(-1) do potęgi n, (a z indeksem dolnym n) =[(-1) do potęgi n] razy n.
Ciąg nazywamy rosnącym, jeżeli jego każdy wyraz, począwszy od drugiego, jest większy od wyrazu bezpośrednio go poprzedzającego, a więc jeżeli dla dowolnej dodatniej liczby całkowitej zachodzi nierówność
Ciąg nazywamy malejącym, jeżeli jego każdy wyraz, począwszy od drugiego, jest mniejszy od wyrazu bezpośrednio go poprzedzającego, a więc jeżeli dla dowolnej dodatniej liczby całkowitej zachodzi nierówność
Ciąg nazywamy stałym, jeżeli wszystkie wyrazy tego ciągu są sobie równe, a więc jeżeli dla dowolnej dodatniej liczby całkowitej zachodzi równość
Ciąg nazywamy niemalejącym, jeżeli jego każdy wyraz, począwszy od drugiego, jest nie mniejszy od wyrazu bezpośrednio go poprzedzającego, a więc jeżeli dla dowolnej dodatniej liczby całkowitej zachodzi nierówność
Ciąg nazywamy nierosnącym, jeżeli jego każdy wyraz, począwszy od drugiego, jest nie większy od wyrazu bezpośrednio go poprzedzającego, a więc jeżeli dla dowolnej dodatniej liczby całkowitej zachodzi nierówność
Jeżeli ciąg jest rosnący, malejący, nierosnący, niemalejący lub stały, to mówimy, że ten ciąg jest monotoniczny. O innych ciągach mówimy, że nie są monotoniczne.
Ciąg określony wzorem nie jest monotoniczny. Wystarczy obliczyć trzy pierwsze wyrazy tego ciągu: , , . Ponieważ i , więc ciąg nie jest monotoniczny.
W tabeli podane zostały wszystkie wyrazy ciągu .
Narysuj wykres ciągu .
Rozstrzygnij, czy ciąg jest monotoniczny.
Ile wyrazów ujemnych występuje w ciągu ?
Ciąg określony jest wzorem .
- Siódmy wyraz tego ciągu jest równy .
- Pierwszym wyrazem dodatnim tego ciągu jest .
Podaj wzór ogólny, jakim może być określony
ciąg siedmiowyrazowy :
ciąg ośmiowyrazowy :
ciąg sześciowyrazowy :
ciąg dziewięciowyrazowy :
Które wyrazy nieskończonego ciągu opisanego wzorem dla są liczbami całkowitymi?
Nieskończony ciąg opisany jest wzorem .
Wyznacz wyraz i wyraz .
Wyznacz wszystkie ujemne wyrazy tego ciągu.
Udowodnij, że dla dowolnej liczby całkowitej dodatniej mamy .
Dany jest ciąg . Czy istnieje wyraz tego ciągu równy ?
Dany jest nieskończony ciąg określony wzorem ogólnym . Które wyrazy tego ciągu są większe od ?
Oblicz piąty wyraz ciągu określonego następująco oraz dla dowolnej liczby całkowitej .
Ciąg określony jest wzorem .
Oblicz wartość wyrażenia .
Określ monotoniczność ciągu .
Ile wyrazów nieskończonego ciągu określonego wzorem należy do przedziału ?
Niech oznacza liczbę wszystkich naturalnych dzielników dodatniej liczby całkowitej , gdzie. Sporządź wykres ciągu . Który wyraz tego ciągu jest największy?
Dane są ciągi i o wzorach ogólnych i .
Sumą ciągów i nazywamy ciąg o wzorze ogólnym .
Różnicą ciągów i nazywamy ciąg o wzorze ogólnym .
Iloczynem ciągów i nazywamy ciąg o wzorze ogólnym .
Ilorazem ciągów i nazywamy ciąg o wzorze ogólnym . Ciąg jest określony dla dowolnej dodatniej liczby całkowitej , ponieważ żaden wyraz ciągu nie jest równy .
Ile wyrazów dodatnich ma ciąg ?
Który wyraz ciągu jest równy zero?
Czy liczba jest jednym z wyrazów ciągu ?
Które wyrazy ciągu są mniejsze od ?
Czy ciąg jest monotoniczny?
Wyznacz wszystkie wartości , dla których prawdziwa jest równość .
Wykaż, że trzeci wyraz ciągu jest kwadratem liczby naturalnej.
W nieskończonym ciągu każdy wyraz, począwszy od drugiego, jest dwa razy większy od różnicy wyrazu poprzedniego i liczby . Wyraz . Oblicz wyrazy ciągu od pierwszego do szóstego.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DpLrb1VJR

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DpLrb1VJR

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DpLrb1VJR
Połącz w pary.
<span aria-label="jeden, plus, początek ułamka, jeden, mianownik, n, koniec ułamka" role="math"><math><mn>1</mn><mo>+</mo><mfrac><mn>1</mn><mi>n</mi></mfrac></math></span>, <span aria-label="dwa, plus, początek ułamka, nawias, minus, jeden zamknięcie nawiasu indeks górny, n, mianownik, n, koniec ułamka" role="math"><math><mn>2</mn><mo>+</mo><mfrac><mrow><mo>(</mo><mo>-</mo><mn>1</mn><msup><mo>)</mo><mi>n</mi></msup></mrow><mi>n</mi></mfrac></math></span>, <span aria-label="dwa, minus, początek ułamka, jeden, mianownik, n, koniec ułamka" role="math"><math><mn>2</mn><mo>-</mo><mfrac><mn>1</mn><mi>n</mi></mfrac></math></span>, <span aria-label="początek ułamka, dwa, mianownik, n, koniec ułamka" role="math"><math><mfrac><mn>2</mn><mi>n</mi></mfrac></math></span>, <span aria-label="jeden, plus, początek ułamka, nawias, minus, jeden zamknięcie nawiasu indeks górny, n, mianownik, n, koniec ułamka" role="math"><math><mn>1</mn><mo>+</mo><mfrac><mrow><mo>(</mo><mo>-</mo><mn>1</mn><msup><mo>)</mo><mi>n</mi></msup></mrow><mi>n</mi></mfrac></math></span>




