Przedstawiono prezentację multimedialną. Slajd 1. Obliczenia symboliczne, działania na wyrażeniach matematycznych. W matematyce możemy wykonywać obliczenia numeryczne lub symboliczne. Obliczenia numeryczne to takie, w których działamy na liczbach i wynikiem jest konkretna wartość. Obliczenia symboliczne to te, kiedy działamy na przykład na wyrażeniach algebraicznych czy przekształcamy wzory, nie podstawiając konkretnych wartości. Slajd 2. Przykład 1. Dany jest graniastosłup prawidłowy czworokątny o przekątnej podstawy długości p oraz kącie nachylenia przekątnej graniastosłupa do płaszczyzny podstawy alfa. Wyznacz sumę długości wszystkich krawędzi tego graniastosłupa w zależności od podanych p i alfa. Slajd 3. Na rysunku przedstawiono graniastosłup prawidłowy czworokątny. Podstawę graniastosłupa oznaczono wielkimi literami alfabetu od A do D, oraz górną wielkimi literami od E do H. Odpowiednio nad wierzchołkiem A, znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F i tak dalej. Zaznaczono kąt alfa między przekątną p podstawy a przekątną graniastosłupa. Długość krawędzi podstawy oznaczono a, natomiast długość krawędzi bocznej oznaczono h. Obok zapisano równanie. $S=8a+4h$. Slajd 4. Długość krawędzi podstawy, oraz długość krawędzi bocznej graniastosłupa przedstawimy za pomocą p oraz alfa. Skorzystamy z zależności trygonometrycznych w trójkącie BDH. Zapiszemy. $\tan \alpha =\frac{h}{p}$. Stąd. $h=p\times \tan \alpha$. Slajd 5. Zauważmy, że jednocześnie p jest przekątną kwadratu w podstawie o boku równym a. Stąd otrzymujemy równanie $a=\frac{p}{\sqrt{2}}$. Slajd 6. Wstawiamy wyznaczone wyrażenia do wzoru na sumę długości wszystkich krawędzi graniastosłupa prawidłowego czworokątnego. $S=8\times \frac{p}{\sqrt{2}}+4\times p\times \tan \alpha =4\sqrt{2}p+4p\tan \alpha =4p\left(\sqrt{2}+\tan \alpha \right)$. To wyrażenie jest odpowiedzią w naszym zadaniu. Slajd 7. Przykład 2. 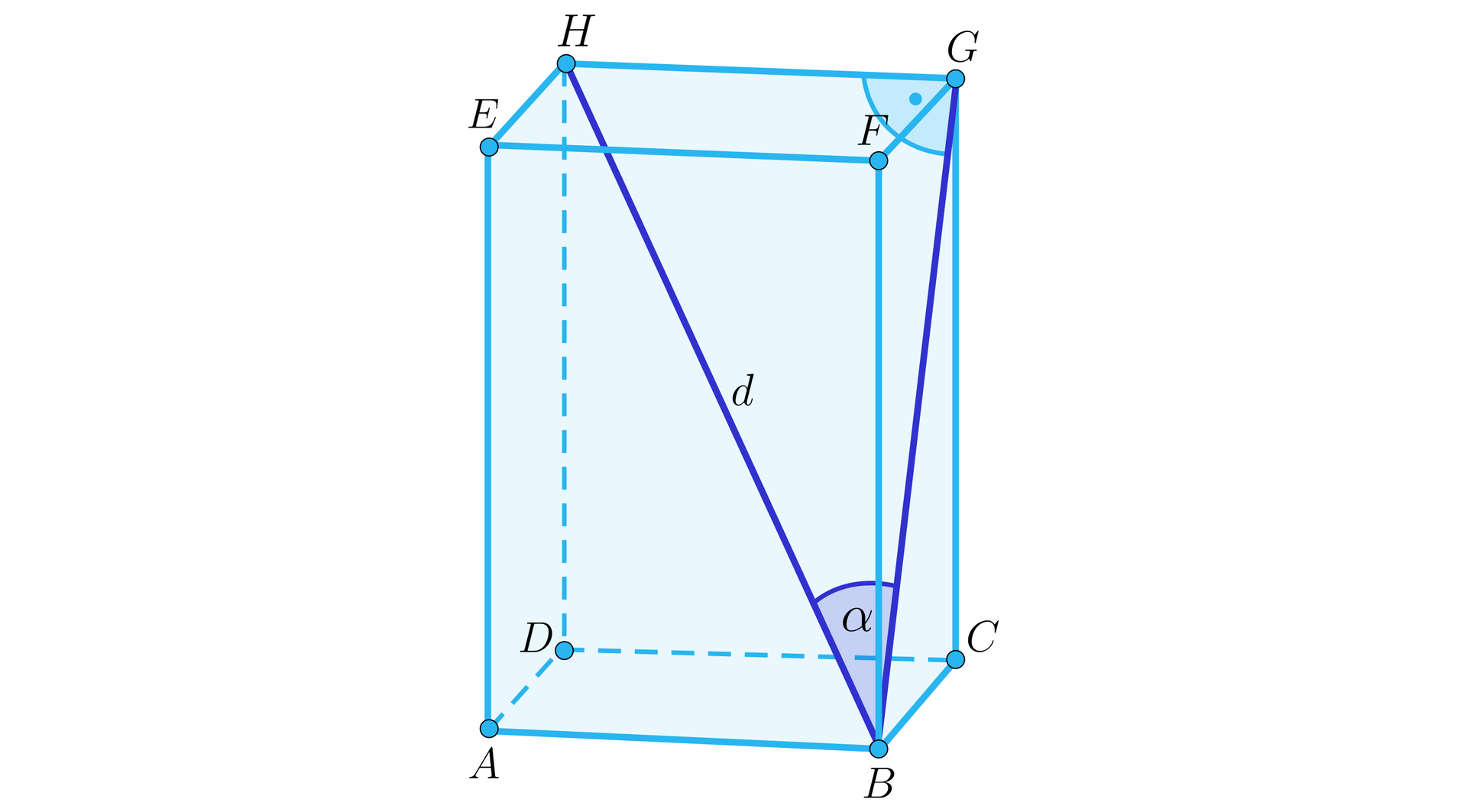Dany jest graniastosłup prawidłowy czworokątny o przekątnej długości d, oraz kącie nachylenia przekątnej graniastosłupa do ściany bocznej alfa. Wykaż, że długość krawędzi bocznej tej bryły jest równa $h=d\sqrt{\cos 2\alpha }$. Na rysunku przedstawiono graniastosłup prawidłowy czworokątny. Podstawę graniastosłupa oznaczono wielkimi literami alfabetu od A do D, oraz górną wielkimi literami od E do H. Odpowiednio nad wierzchołkiem A, znajduje się wierzchołek E, nad wierzchołkiem B wierzchołek F i tak dalej. Przez a oznaczono długość krawędzi podstawy, natomiast przez h długość krawędzi bocznej. Zaznaczono kąt alfa między przekątną d graniastosłupa, a przekątną BG ściany bocznej. $\angle BGH$ jest kątem prostym. Slajd 8. Korzystając z zależności trygonometrycznych w trójkącie $BGH$ otrzymujemy. $\sin \alpha =\frac{a}{d}$, co po przekształceniu daje nam $a=d\times \sin \alpha$. Wyznaczamy także równanie. $\cos \alpha =\frac{długość odcinka BG}{d}$. Stąd otrzymujemy, że długości odcinka BG równa się $d\times \cos \alpha$. Slajd 9. Korzystamy z twierdzenia pitagorasa w trójkącie $BCG$ i jednego ze wzorów na cosinus podwojonego kąta. Stąd otrzymujemy równanie. $a^2+h^2= długość odcinka BG podniesiona do kwadratu$. Następnie. $a^2+h^2=d^2{\cos }^2\alpha$. Następnie. $h^2=d^2{\cos }^2\alpha -d^2{\sin }^2\alpha$. Dalej wyłączamy przed nawias. $h^2=d^2\left({\cos }^2\alpha -{\sin }^2\alpha \right)$. Następnie otrzymujemy. $\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha$. Dalej. $h^2=d^2\times \cos 2\alpha$. Otrzymujemy $h=d\sqrt{\cos 2\alpha }$ co należało dowieść.